Présentation du jeu¶

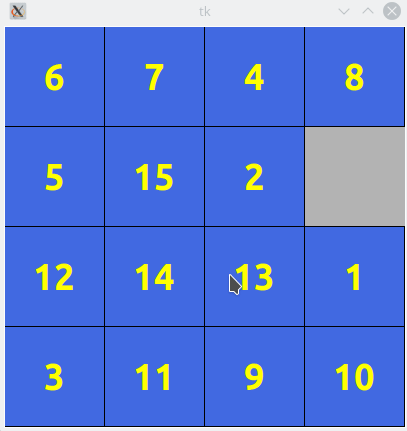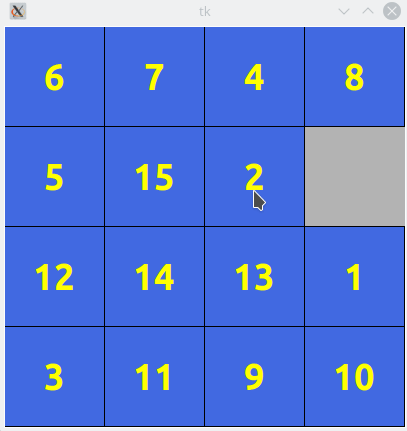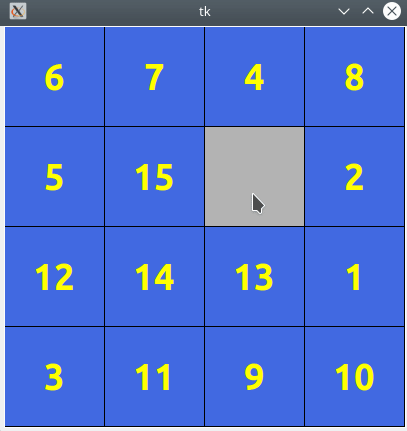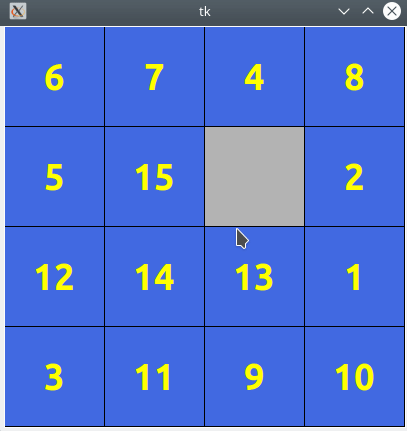
Le jeu de taquin est un puzzle constitué de 15 tuiles carrées numérotées de 1 à 15, placées sur un plateau 4x4 et qui se déplacent par glissement :

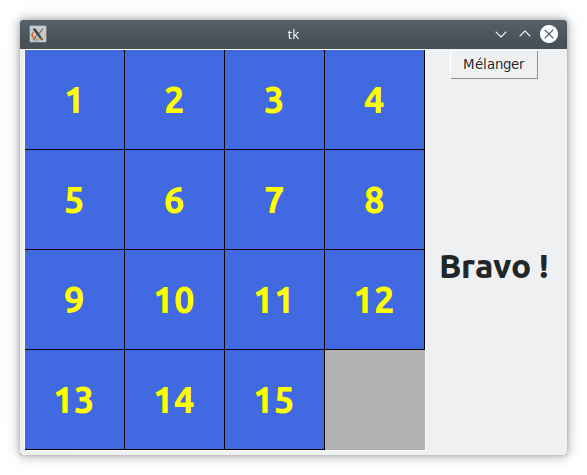
Au départ, les pièces sont mélangées et le but du jeu est de les réorganiser pour qu’elles se suivent dans l’ordre de 1 à 15 :

On appelle parfois ce jeu le « pousse-pousse » et le jeu est connu en anglais sous le nom de fifteen-puzzle.

Le jeu existe en version matérielle (bois, plastique, métal). Il existe aussi en version logicielle. Par exemple, il y avait un taquin sous le nom de Picture Puzzle au moment de la sortie du système d’exploitation Windows 7 et qui était incorporé dans les Desktop Gadgets. Il existe aussi de nombreuses versions de ce jeu sous Android. Sur le web, voici un taquin agréable à jouer et écrit en javascript (toutefois, à l’usage, je me rends compte qu’il y a un bug dans certains déplacements à la souris).

A regarder plus en détail, il apparaît qu’il existe 4 possibilités de déplacement des tuiles :

• un mode séquentiel : le déplacement n’est pas progressif, il se fait par à-coups, typiquement cette version ;
• un mode progressif : le déplacement est continu, fluide, ici ;
• un mode séquentiel et multi-déplacement : on peut déplacer par à-coups plusieurs tuiles en une fois ;
• un mode progressif et multi-déplacement (présenté dans la démo).

Présentation de l’activité¶

L’activité consiste à écrire sous Tkinter un taquin pleinement jouable. L’interface finale a été montrée ci-dessus.

Les étapes pour y parvenir seront les suivantes :

• dessiner un taquin statique
• analyser le déplacement d’une tuile seule
• obtenir un « taquin séquentiel »
• créer une fonction de mélange
• créer un bouton pour réinitialiser le jeu
• implémenter le déplacement progressif (glissement) de chaque tuile
• analyser le multi-déplacement de tuiles
• implémenter un taquin supportant le multi-déplacement séquentiel
• implémenter un taquin supportant le multi-glissement.

Afin de simplifier la présentation, je me limiterai à l’implémentation d’un taquin 4 x 4. Chaque tuile (carrée) aura toujours une dimension de 100 pixels. Le code contiendra donc des « constantes magiques » telle que 100, 50, 16, 17, 4, etc. Dans un code soigné, on doit néanmoins éviter le recours à des constantes magiques et on doit utiliser des variables lisibles permettant d’adapter le jeu à d’autres situations.

Si vous arrivez jusqu’à la réalisation du premier taquin (avec bouton mélangeur et annonce de victoire), vous pouvez considérer que vous avez fait l’essentiel de l’activité.

Dessiner un taquin statique¶

Toutes les informations concernant le jeu que Tkinter va dessiner sur le canevas proviendront d’un tableau 2D appelé board et de taille 4x4 (le modèle). L’interface graphique (la vue) sera un miroir de ce tableau. À la ligne d’indice i et à la colonne d’indice j de board, on trouvera une valeur (par exemple 12) qui est la valeur de la tuile sur le plateau de jeu. La case vide sera marquée par la valeur 16. Dans beaucoup d’exemples, le plateau board initial sera le suivant :

board=[[6, 7, 4, 8],
       [5, 15, 13, 2],
       [12, 14, 9, 1],
       [3, 11, 10, 16]]

Maintenant, on va dessiner un simple plateau de jeu dans un canevas Tkinter :

Pour dessiner une tuile du taquin, on dessine un carré avec la méthode create_rectangle du canevas et pour faire apparaître le nombre sur la tuile, on utilise la méthode create_text.

Le code qui suit dessine un taquin statique :

taquin_statique.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

from tkinter import *

board=[[6, 7, 4, 8],
       [5, 15, 13, 2],
       [12, 14, 9, 1],
       [3, 11, 10, 16]]

FONT=('Ubuntu', 27, 'bold')
master=Tk()
cnv=Canvas(master, width=400, height=400, bg='gray70')
cnv.pack()

for i in range(4):
    for j in range(4):
        x, y=100*j, 100*i
        A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
        cnv.create_rectangle(A, B, fill="royal blue")
        cnv.create_text(C, text=board[i][j], fill="yellow",
                            font=FONT)
master.mainloop()

• Ligne 8 : FONT est la police qui va être utilisée pour afficher les nombres. J’ai choisi la taille en fonction du rendu sur mon système, ça peut-être différent chez vous.
• Lignes 9-11 : on crée une fenêtre (master) et un canevas cnv que l’on insère dans la fenêtre.
• Lignes 13-19 : à l’aide d’une double boucle, on dessine les tuiles du taquin (lignes 17 et 18). La valeur board[i][j] est affichée sur la tuile (ligne 18, option text); bien que cette valeur soit un entier (type int), Tkinter la convertit en chaîne de caractères.
• Ligne 16 : on définit les coins A et B de la tuile courante, son centre C et on dessine le rectangle (ligne 17) puis le texte (ligne 18).

La case vide¶

On observe sur le dessin qu’il n’y a pas de case vide. Sans surprise, pour faire apparaître la case vide, il suffit d’effacer la dernière tuile créée :

Pour effacer un item du canevas, on dispose de la méthode delete. Pour désigner l’item qui doit être effacé, il suffit de donner à la méthode l’id de l’item.

Le code complet est :

taquin_statique_effacer.py

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

from tkinter import * board=[[6, 7, 4, 8], [5, 15, 13, 2], [12, 14, 9, 1], [3, 11, 10, 16]] FONT=('Ubuntu', 27, 'bold') master=Tk() cnv=Canvas(master, width=400, height=400, bg='gray70') cnv.pack() for i in range(4): for j in range(4): x, y=100*j, 100*i A, B, C=(x, y), (x+100, y+100), (x+50, y+50) rect = cnv.create_rectangle(A, B, fill="royal blue") txt = cnv.create_text(C, text=board[i][j], fill="yellow", font=FONT) cnv.delete(rect) cnv.delete(txt) master.mainloop()

Le code aux lignes 21 et 22 fonctionne car lorsque la double for se termine (ligne 19), dans les variables rect et txt (lignes 17 et 18) on trouve les id de la dernière tuile qui a été dessinée, celle numérotée 16 et que l’on veut justement effacer.

Identifier les tuiles¶

Lorsqu’on va coder le jeu, certaines fonctions auront besoin de savoir quel est le numéro d’une tuile qui a réceptionné un clic. Plusieurs méthodes sont possibles pour arriver à ce résultat. Ici, on va construire une liste items de taille 17=16+1 et telle que items[k] contienne les id de la tuile numérotée k. Plus précisément, et par exemple, items[12] contiendra un tuple de la forme (rect, txt) où rect est l’id du rectangle de la tuile numérotée 12 et txt l’id du texte ( à savoir le nombre "12") sur cette tuile.

items.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

from tkinter import *

board=[[6, 7, 4, 8],
       [5, 15, 13, 2],
       [12, 14, 9, 1],
       [3, 11, 10, 16]]

FONT=('Ubuntu', 27, 'bold')
master=Tk()
cnv=Canvas(master, width=400, height=400, bg='gray70')
cnv.pack()

items=[None for i in range(17)]

for i in range(4):
    for j in range(4):
        x, y=100*j, 100*i
        A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
        rect=cnv.create_rectangle(A, B, fill="royal blue")
        nro=board[i][j]
        txt=cnv.create_text(C, text=nro, fill="yellow",
                            font=FONT)
        items[nro]=(rect, txt)
cnv.delete(rect)
cnv.delete(txt)
master.mainloop()

• Ligne 13 : la liste des items à remplir contient 17 éléments et non pas 16 : en effet, l’indice dans la liste items doit correspondre au numéro de la tuile et les numéros commencent à 1 et pas à 0.
• Ligne 23 : à chaque construction de tuile, on place à l’indice k de items un tuple (tile, txt) contenant les id de la tuile de numéro k.

Lorsqu’une zone sur le plateau de jeu réceptionne un clic, on passera par les étapes suivantes :

• on calculera la position (i, j) ligne x colonne sur le plateau de jeu,
• on ira regarder dans le tableau 2D board, à la position ligne i et colonne j, quel est le numéro de la tuile ;
• grâce à la liste items, on aura accès aux id dans le plateau Tkinter de la tuile numérotée k ce qui permettra de déplacer la tuile, etc.

Dans le code ci-dessous, on implémente la technique précédente : si l’utilisateur clique sur le plateau de jeu, l’indice de ligne et de colonne est affiché et le numéro porté par la tuile aussi ce qui montre :

lire_ligne_col.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

from tkinter import *

def clic(event):
    i=event.y//100
    j=event.x//100
    print("ligne=", i, "colonne=", j,"nro=", board[i][j])

board=[[6, 7, 4, 8],
       [5, 15, 13, 2],
       [12, 14, 9, 1],
       [3, 11, 10, 16]]

FONT=('Ubuntu', 27, 'bold')
master=Tk()
cnv=Canvas(master, width=400, height=400, bg='gray70')
cnv.pack()

cnv.bind("<Button-1>",clic)

items=[None for i in range(17)]

for i in range(4):
    for j in range(4):
        x, y=100*j, 100*i
        A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
        rect=cnv.create_rectangle(A, B, fill="royal blue")
        nro=board[i][j]
        txt=cnv.create_text(C, text=nro, fill="yellow",
                            font=FONT)
        items[nro]=(rect, txt)
cnv.delete(rect)
cnv.delete(txt)
master.mainloop()

• Quand le canevas reçoit un clic (ligne 18), la fonction clic est appelé (lignes 3-6).

• Lignes 4-5 :

  • (event.x, event.y) sont les coordonnées du clic sur le canevas.
  • comme chaque tuile est un carré de côté 100 pixels, les divisions donnent bien les indices de ligne et de colonne. Noter l’inversion : event.x fournit j et non pas i.

• Ligne 6 : board[i][j] contient le numéro de la tuile placé aux indices i et j.

Enfin, montrons comment on peut agir sur une tuile grâce à la liste items. Ici, en guise d’illustration, on décide par exemple de colorier en rouge la tuile sur laquelle on clique :

colorier_tuile.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

from tkinter import *

def clic(event):
    i=event.y//100
    j=event.x//100
    nro=board[i][j]
    rect, txt = items[nro]
    cnv.itemconfigure(rect, fill="red")

board=[[6, 7, 4, 8],
       [5, 15, 13, 2],
       [12, 14, 9, 1],
       [3, 11, 10, 16]]

FONT=('Ubuntu', 27, 'bold')
master=Tk()
cnv=Canvas(master, width=400, height=400, bg='gray70')
cnv.pack()

cnv.bind("<Button-1>",clic)

items=[None for i in range(17)]

for i in range(4):
    for j in range(4):
        x, y=100*j, 100*i
        A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
        rect=cnv.create_rectangle(A, B, fill="royal blue")
        board[i][j]
        nro=board[i][j]
        txt=cnv.create_text(C, text=nro, fill="yellow",
                            font=FONT)
        items[nro]=(rect, txt)
cnv.delete(rect)
cnv.delete(txt)
master.mainloop()

• Lignes 6-7 : une fois récupéré le numéro de la tuile cliquée, on dispose par exemple de l’id du rectangle correspondant à la tuile.
• Ligne 8 : on peut alors changer des options du rectangle, comme sa couleur fill, grâce à la méthode itemconfigure.

Le déplacement de pièce¶

Si on observe un taquin

on se rend compte qu’à tout instant du jeu si une tuile peut se déplacer, elle ne peut le faire que d’une seule façon : en prenant la place de la case libre (qui est toujours unique). Par exemple, ci-dessus, il y a trois déplacements possibles :

• soit on déplace la tuile n°2, forcément vers la droite,
• soit on déplace la tuile n°1, forcément vers le haut,
• soit on déplace la tuile n°8, forcément vers le bas.

Ainsi, au lieu d’accompagner le déplacement de la tuile dans la direction de la case vide comme on le ferait manuellement, il suffira au joueur de cliquer sur la tuile voulue pour provoquer son (seul) déplacement possible.

Du point de vue du code, la case vide est représentée par le numéro 16. Donc déplacer une tuile, disons k, revient à échanger k avec 16 dans board. Par exemple, dans le dessin ci-dessus, le déplacement de la tuile n°2 s’écrit :

board[1][2], board[1][3] = board[1][3], board[1][2]

En effet, on rappelle qu’en Python, l’échange de deux références u et v se fait par u, v = v, u.

Du point de vue de Tkinter, un déplacement se fait exactement comme dans le jeu physique : il est tout simplement obtenu en appliquant la méthode move à une tuile et donc en fait aux deux items du canevas qui la constituent : le rectangle et le texte.

Déplacer une tuile seule¶

On va regarder maintenant comment déplacer une tuile à la souris. Pour cela, on va examiner une situation simplifiée d’un plateau avec une seule tuile portant un texte et quand on clique sur la tuile, elle se déplace à droite :

Le code correspondant est :

deplacer.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

from tkinter import *

def clic(event):
    global j_tile
    i=event.y//100
    j=event.x//100
    if i==i_tile and j==j_tile:
        cnv.move(tile, 100, 0)
        cnv.move(txt, 100, 0)
        j_tile+=1

FONT=('Ubuntu', 27, 'bold')
master=Tk()
cnv=Canvas(master, width=600, height=400, bg='gray70')
cnv.pack()

cnv.bind("<Button-1>",clic)

i=2
j=1

x, y=100*j, 100*i
A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
tile=cnv.create_rectangle(A, B, fill="royal blue")
txt=cnv.create_text(C, text="OK !", fill="yellow", font=FONT)

i_tile=i
j_tile=j

master.mainloop()

On définit une tuile carrée marquée OK de côté 100 pixels (lignes 22-25). Elle est placée dans notre grille en ligne d’indice 2 et en colonne d’indice 1 (lignes 19-20 et 27-28). Quand on clique sur le canevas (ce qui se traduit par l’événement "<Button-1>", cf. ligne 17), la fonction clic est appelée (lignes 3-10). Cette fonction

• identifie la ligne et la colonne du point cliqué (lignes 5-6)
• examine si c’est la tuile qui a été cliquée (ou pas) (ligne 7)
• déplace la tuile d’un vecteur de coordonnées (100, 0) autrement dit 100 pixels à droite et 0 pixel vers le bas (Lignes 8-9).

Si on clique ailleurs que sur la tuile, l’exécution, arrivée ligne 7, quitte la fonction clic et il ne se passe rien.

Le programme sait où est positionnée la tuile grâce aux variables globales i_tile et j_tile (cf. lignes 27-28 et ligne 4) qui donnent la ligne et la colonne où se trouve la tuile. D’autre part, une fois la tuile identifiée, il n’y a pas de difficulté à accéder (lignes 8-9) à ses id (rectangle et texte) puisqu’elles sont en variables globales (lignes 24-25).

Une fois que la tuile a bougé, il faut mettre à jour sa nouvelle position. Pour cela, on modifie la variable j_tile en incrémentant de 1 (ligne 10) puisque la tuile est ici déplacée uniquement vers la droite (et donc, l’indice de ligne i_tile n’a pas être mis-à-jour). Comme j_tile est une variable globale, nous sommes obligés pour la modifier (ligne 10) de la déclarer en global (ligne 4).

C’est exactement ce principe que l’on va mettre en œuvre pour créer notre premier taquin jouable.

Premier taquin jouable¶

Le déplacement d’une tuile est la fonctionnalité essentielle d’un taquin. Techniquement, pour déplacer une tuile sur un taquin, il faut :

• déterminer la position ligne x colonne qui réceptionne le clic ;

• ignorer le clic

  • s’il est sur la case vide ;
  • si aucune case voisine de \(\mathtt{T}\) (la tuile choisie) n’est la case vide

• si une des cases voisines est vide, déplacer la tuile \(\mathtt{T}\) dans cette case et mettre à jour la position de la case vide.

Pour savoir si un tuile T, placée en position ligne x colonne (i, j), peut bouger, il suffit de s’assurer que l’une de ses quatre voisines est la case vide. Dans tous les codes qui suivent, la position ligne x colonne de la case vide est placée dans des variables (globales) i_empty et j_empty.

La méthode la plus directe consiste à tester successivement si :

• la case vide est immédiatement à droite de T
• la case vide est immédiatement à gauche de T
• la case vide est immédiatement au-dessous de T
• la case vide est immédiatement au-dessus de T.

Si on n’est pas dans l’une de ces 4 situations, c’est qu’on a cliqué sur une case qui est immobile ou sur la case vide.

Pour tester, par exemple, si la case vide est immédiatement à droite de T, il suffit d’examiner la valeur de

j + 1 == j_empty and i == i_empty

Si ce booléen vaut True, c’est que la case vide est juste à droite de T et pour déplacer la tuile, il suffit de déplacer avec la méthode move les items rectangle et texte suivant le vecteur (100, 0) pixels. C’est analogue pour les 3 autres situations.

Noter que ces 4 situations doivent être traitées par une suite de if/elif et pas une suite de if puisque les conditions s’excluent.

D’où le code suivant qui fournit un premier taquin pleinement jouable :

taquin_sequentiel.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

from tkinter import *

def clic(event):
    global i_empty, j_empty
    i=event.y//100
    j=event.x//100
    nro=board[i][j]
    rect, txt=items[nro]
    if j+1 ==j_empty and i==i_empty:
        cnv.move(rect, 100, 0)
        cnv.move(txt, 100, 0)
    elif j-1 ==j_empty and i==i_empty:
        cnv.move(rect, -100, 0)
        cnv.move(txt, -100, 0)
    elif i+1 ==i_empty and j==j_empty:
        cnv.move(rect, 0, 100)
        cnv.move(txt, 0, 100)
    elif i-1 ==i_empty and j==j_empty:
        cnv.move(rect, 0, -100)
        cnv.move(txt, 0, -100)
    else:
        return
    board[i][j],board[i_empty][j_empty]=(
        board[i_empty][j_empty],board[i][j])
    i_empty=i
    j_empty=j

items=[None for i in range(17)]
board=[[6, 7, 4, 8],
       [5, 15, 13, 2],
       [12, 14, 9, 1],
       [3, 11, 10, 16]]

FONT=('Ubuntu', 27, 'bold')
master=Tk()
cnv=Canvas(master, width=400, height=400, bg='gray70')
cnv.pack(side='left')

i_empty, j_empty=3,3

for i in range(4):
    for j in range(4):
        x, y=100*j, 100*i
        A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
        rect=cnv.create_rectangle(A, B, fill="royal blue")
        nro=board[i][j]
        txt=cnv.create_text(C, text=nro, fill="yellow",
                            font=FONT)
        items[nro]=(rect, txt)

cnv.delete(txt)
cnv.delete(rect)

cnv.bind("<Button-1>",clic)

master.mainloop()

• Lignes 5-6 : la position ligne x colonne (i, j) est là où une tuile a reçu un clic.

• Lignes 7-8 : on récupère le numéro de la tuile et les deux id d’items qui forment une tuile

• On examine successivement si la tuile peut aller

  • à droite (lignes 9-11)
  • à gauche (ligne 12-14)
  • en bas (ligne 15-17)
  • en haut (ligne 18-20).

• Si aucune des conditions précédentes n’est satisfaite (ligne 21), on quitte la fonction clic (ligne 22) ;

• Dans tout cas de déplacement, on met à jour le plateau board (lignes 23-24) ainsi que la case vide (lignes 25-26)

• Le reste du code est inchangé par rapport à lire_ligne_col.py.

Mélanger le plateau de jeu¶

Bien sûr, avec un vrai taquin, quand on commence à jouer, le plateau a été préalablement mélangé. Dans notre cas, le mélange va être effectué dans le tableau board et l’affichage par Tkinter répercutera visuellement ce mélange.

La première méthode qui vient à l’esprit est de mélanger une liste de 16 nombres puis de les placer dans board par paquets de 4 dans chaque ligne, comme ci-dessous :

from random import shuffle

nros=[k for k in range(1, 17)]
shuffle(nros)

board=[[nros[4*i+j] for j in range(4)] for i in range(4)]

print(*board, sep='\n')

[15, 6, 11, 5]
[10, 2, 1, 3]
[12, 16, 9, 13]
[4, 14, 7, 8]

• Pour mélanger une liste, on utilise la fonction shuffle du module random (lignes 1 et 4)
• On regroupe ensuite (ligne 6) le mélange par paquets de 4 que l’on place dans les lignes du tableau 2D.

Toutefois, rien ne garantit a priori que n’importe quel mélange des tuiles obtenu de cette façon pourra être réordonné convenablement par glissements des tuiles. Et justement, il se trouve que certains mélanges ne peuvent être résolus : c’est le fameux problème de Sam Loyd.

D’ailleurs, certaines versions en ligne ont ce bug, par exemple sur le site 15puzzle, le jeu peut se terminer ainsi :

Finalement, pour mélanger le plateau, on va donc procéder comme on le ferait avec un taquin matériel. Partant d’un taquin ordonné, il suffit d’échanger suffisamment de fois la case vide (numéro 16 dans board) et une case voisine (dans board) :

melanger.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

from random import randrange

def voisins(n, i, j):
    return [(a,b) for (a, b) in
            [(i, j+1),(i, j-1), (i-1, j), (i+1,j)]
            if a in range(n) and b in range(n)]

def echange(board, empty):
    i, j=empty
    V=voisins(4, i, j)
    ii, jj=V[randrange(len(V))]
    board[ii][jj], board[i][j]=board[i][j],board[ii][jj]
    return ii, jj

def melanger(N):
    board=[[4*lin+1+col for col in range(4)]
        for lin in range(4)]
    print(*board, sep='\n')

    empty=(3,3)

    for i in range(N):
        empty=echange(board, empty)
    print('-----------')
    print(*board, sep='\n')

melanger(200)

28
29
30
31
32
33
34
35
36

[1, 2, 3, 4]
[5, 6, 7, 8]
[9, 10, 11, 12]
[13, 14, 15, 16]
-----------
[13, 8, 2, 12]
[6, 7, 9, 3]
[1, 15, 5, 10]
[14, 11, 4, 16]

• Lignes 16-17 et 28-31 : avec une liste en compréhension, on crée un plateau rempli avec les entiers de 1 à 16.
• Lignes 22-23 : on effectue N échanges successifs de 16 et d’une de ses voisines
• Pour chaque échange, on part de la case vide (on la connait, cf. ligne 20). On construit la liste des voisines de la case vide (lignes 10 et 3-6) et on en choisit une au hasard (ligne 11).
• On déplace la tuile choisie dans la vase vide (ligne 12), ce qui revient à échanger les positions dans board.
• On renvoie la nouvelle position de la case vide (ligne 13) ce qui évite de la rechercher quand on fait un nouvel échange (ligne 23).

En pratique, il faut choisir N assez grand pour obtenir un bon mélange. Par exemple, si vous examinez le taquin sur ce site pour lequel il semble que N=200 ait été choisi vous observerez que bien souvent une case n’est jamais bien loin de sa case initiale. Dans la sortie ci-dessus où N=200 a aussi été choisi, aucune tuile n’est à plus d’une distance de 3 de sa position initiale (la distance est la distance de Manhattan de déplacement sur une grille, autrement dit, c’est le nombre de coups minimal), sur un maximum de 6 possibles.

Voici une sortie pour N=1000 :

[10, 13, 9, 3]
[11, 8, 15, 4]
[16, 2, 5, 6]
[7, 14, 1, 12]

On observe que les quatre tuiles 1, 7, 9 et 13 sont à une distance d’au moins 4 de leur position d’origine, c’est mieux.

Amélioration mineure¶

Noter que le mélange place la case vide n’importe où sur le plateau alors qu’on pourrait souhaiter que la case vide soit toujours au même endroit, en bas à droite. Pour remédier à cela, il suffit de déplacer la case vide dans le coin en effectuant au plus deux déplacements de blocs de tuiles comme visible ci-dessous :

On va donc écrire une fonction normal qui, en deux étapes, place la case vide dans le coin inférieur droit (« normalise »). Pour cela, la case vide est déplacée dans la ligne du bas puis, dans un 2e temps, déplacée dans la dernière colonne :

1 2 3 4 5 6 7 8 9 10

def normal(board, empty): i_empty, j_empty = empty for i in range(i_empty, 4): (board[i][j_empty], board[i_empty][j_empty])= ( board[i_empty][j_empty], board[i][j_empty]) i_empty=i for j in range(j_empty, 4): board[i_empty][j], board[i_empty][j_empty]= ( board[i_empty][j_empty],board[i_empty][j]) j_empty=j

• Lignes 3-5 : déplacement de la case vide dans la dernière ligne par une suite d’échanges sur le plateau board.
• Ligne 6 : à chaque étape, la variable pointant vers la case vide est mise à jour
• Ligne 7-10 : on fait de même sauf qu’on place la case vide dans la colonne de droite.

Voici un code effectuant le mélange complet :

melange_plus.py

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

from random import randrange def voisins(n, i, j): return [(a,b) for (a, b) in [(i, j+1),(i, j-1), (i-1, j), (i+1,j)] if a in range(n) and b in range(n)] def echange(board, empty): i, j=empty V=voisins(4, i, j) ii, jj=V[randrange(len(V))] board[ii][jj], board[i][j]=board[i][j],board[ii][jj] return ii, jj def normal(board, empty): i_empty, j_empty = empty for i in range(i_empty, 4): (board[i][j_empty], board[i_empty][j_empty])= ( board[i_empty][j_empty], board[i][j_empty]) i_empty=i for j in range(j_empty, 4): board[i_empty][j], board[i_empty][j_empty]= ( board[i_empty][j_empty],board[i_empty][j]) j_empty=j def melanger(N): board=[[4*lin+1+col for col in range(4)] for lin in range(4)] empty=(3,3) for i in range(N): empty=echange(board, empty) normal(board, empty) print(*board, sep='\n') melanger(500)

40 41 42 43

[10, 7, 6, 4] [9, 3, 1, 14] [12, 5, 2, 13] [15, 11, 8, 16]

• La sortie : comme on le voit, le plateau est mélangé et la case vide est au coin inférieur droit.
• Ligne 35 : une fois le plateau mélangé, on appelle la fonction normal pour placer la case vide dans le coin.

Ajouter un bouton¶

Pour avoir un jeu rejouable, il reste à ajouter un bouton au canevas contenant notre jeu. Bien que nous ayons déjà tout le code utile, l’ajout va entraîner un nombre important de refactorisations de code.

Ajouter un bouton inactif est assez simple. On repart du code taquin_statique_effacer.py et on rajoute juste un widget avec la méthode pack (lignes 16-17 ci-dessous) :

taquin_bouton_fake.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

from tkinter import *

def f():
    print("TODO")

board=[[6, 7, 4, 8],
       [5, 15, 13, 2],
       [12, 14, 9, 1],
       [3, 11, 10, 16]]

FONT=('Ubuntu', 27, 'bold')
master=Tk()
cnv=Canvas(master, width=400, height=400, bg='gray70')
cnv.pack(side="left")

btn=Button(text="Mélanger", command=f)
btn.pack()

for i in range(4):
    for j in range(4):
        x, y=100*j, 100*i
        A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
        rect=cnv.create_rectangle(A, B, fill="royal blue")
        txt=cnv.create_text(C, text=board[i][j], fill="yellow",
                            font=FONT)
cnv.delete(rect)
cnv.delete(txt)
master.mainloop()

ce qui donne :

Ici, la commande f (lignes 16 et 3-4) ne fait rien quand on clique sur le bouton, si ce n’est qu’elle affiche juste TODO dans la console.

La fonction qui sera exécutée à chaque clic sur le bouton Mélanger va faire en sorte que le jeu reprenne à zéro. Il s’agit donc en fait d’une fonction d”initialisation du jeu et on va l’appeler non pas f mais init. Cette fonction init sera même appelée au premier plateau qui est présenté au joueur.

Donc, à chaque appel de init, il va falloir définir ou redéfinir

• la tableau 2D board,
• la liste items,
• la position ligne et colonne i_empty et j_empty.

Puis il faudra :

• mélanger board avec les fonctions déjà créées,
• afficher le plateau Tkinter,
• récupérer les id des items.

Par ailleurs, suite à un mélange de board, plutôt que déplacer les tuiles déjà créées à leur nouvel emplacement, il est beaucoup plus simple de les effacer et de recréer des tuiles aux nouveaux emplacements.

La fonction init pourrait apparaître ainsi :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def init():
    global i_empty, j_empty, items, board
    cnv.delete("all")
    items=[None]

    board=melanger()
    for i in range(4):
        for j in range(4):
            if board[i][j]==16:
                i_empty, j_empty=i, j

    items=[None for i in range(17)]

    for i in range(4):
        for j in range(4):
            x, y=100*j, 100*i
            A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
            tile=cnv.create_rectangle(A, B, fill="royal blue")
            nro=board[i][j]
            txt=cnv.create_text(C, text=nro, fill="yellow", font=FONT)
            items[nro]=(tile, txt)
    cnv.delete(tile)
    cnv.delete(txt)

• Ligne 3 : le canevas est défini à l’extérieur de la fonction et accessible en lecture sans déclaration particulière.
• Ligne 2 : la fonction init définit un certain nombre de variables utiles à d’autres fonctions du programme, voilà pourquoi, il faut les déclarer en global.
• Ligne 6 : création du tableau 2D des numéros.
• Lignes 7-10 : extraction de la case vide.
• Ligne 12 : items est une liste pré-construite avec 17 éléments (16 numéros et une valeur factice placée à l’indice 0).
• Ligne 3 : comme on recrée les tuiles à chaque mélange, il faut tout effacer (noter qu’il est possible d’effacer même si rien n’a été construit).
• Ligne 21 : la tuile portant le numéro nro est placée à l’indice nro de la liste item.

En incorporant ce code avec les codes précédents, on obtient un 2e taquin pleinement jouable :

taquin_sequentiel_complet.py

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100

from random import randrange
from tkinter import *

def clic(event):
    i=event.y//100
    j=event.x//100
    global i_empty, j_empty
    nro=board[i][j]
    tile, txt=items[nro]
    if j+1 ==j_empty and i==i_empty:
        cnv.move(tile, 100, 0)
        cnv.move(txt, 100, 0)
    elif j-1 ==j_empty and i==i_empty:
        cnv.move(tile, -100, 0)
        cnv.move(txt, -100, 0)
    elif i+1 ==i_empty and j==j_empty:
        cnv.move(tile, 0, 100)
        cnv.move(txt, 0, 100)
    elif i-1 ==i_empty and j==j_empty:
        cnv.move(tile, 0, -100)
        cnv.move(txt, 0, -100)
    else:
        return
    board[i][j],board[i_empty][j_empty]=board[i_empty][j_empty],board[i][j]
    i_empty=i
    j_empty=j

def voisins(n, i, j):
    return [(a,b) for (a, b) in
            [(i, j+1),(i, j-1), (i-1, j), (i+1,j)]
            if a in range(n) and b in range(n)]

def echange(board, empty):
    i, j=empty
    V=voisins(4, i, j)
    ii, jj=V[randrange(len(V))]
    board[ii][jj], board[i][j]=board[i][j],board[ii][jj]
    return ii, jj

def normal(board, empty):
    i_empty, j_empty = empty
    for i in range(i_empty, 4):
        (board[i][j_empty], board[i_empty][j_empty])= (
            board[i_empty][j_empty], board[i][j_empty])
        i_empty=i
    for j in range(j_empty, 4):
        board[i_empty][j], board[i_empty][j_empty]= (
            board[i_empty][j_empty],board[i_empty][j])
        j_empty=j

def melanger(N):
    board=[[4*lin+1+col for col in range(4)]
        for lin in range(4)]

    empty=(3,3)

    for i in range(N):
        empty=echange(board, empty)
    return board

def init(N=500):
    global i_empty, j_empty, items, board
    cnv.delete("all")
    items=[None]

    board=melanger(N)
    for i in range(4):
        for j in range(4):
            if board[i][j]==16:
                i_empty, j_empty=i, j
    empty=i_empty, j_empty
    normal(board, empty)
    i_empty, j_empty=3,3
    items=[None for i in range(17)]

    for i in range(4):
        for j in range(4):
            x, y=100*j, 100*i
            A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
            rect=cnv.create_rectangle(A, B, fill="royal blue")
            nro=board[i][j]
            txt=cnv.create_text(C, text=nro, fill="yellow",
                                font=FONT)
            items[nro]=(rect, txt)
    rect, txt=items[16]
    cnv.delete(txt)
    cnv.delete(rect)

FONT=('Ubuntu', 27, 'bold')
master=Tk()
cnv=Canvas(master, width=400, height=400, bg='gray70')
cnv.pack(side='left')

btn=Button(text="Mélanger", command=init)
btn.pack()

cnv.bind("<Button-1>",clic)
init()

master.mainloop()

Détection de la position gagnante¶

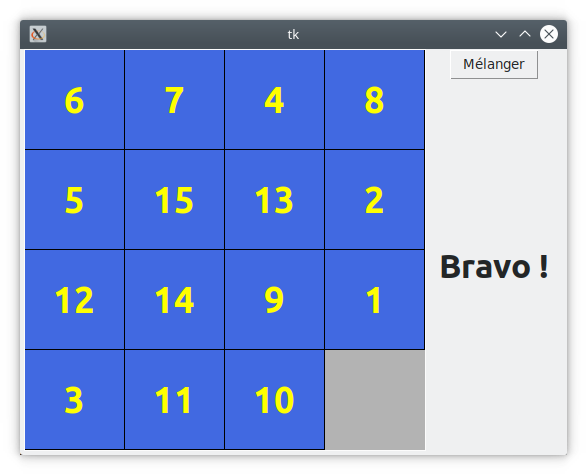
On voudrait envoyer un message de félicitation au joueur lorsqu’il a terminé son taquin. Ce message apparaîtra sous la forme suivante :

En outre, le plateau sera bloqué après la victoire car cela n’a plus de sens de le modifier.

Pour afficher le message, on utilise un label Tkinter. Voici ce que cela donne hors-contexte de victoire :

victoire_fake.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

from tkinter import *

def f():
    print("TODO")

board=[[6, 7, 4, 8],
       [5, 15, 13, 2],
       [12, 14, 9, 1],
       [3, 11, 10, 16]]

FONT=('Ubuntu', 27, 'bold')
master=Tk()
cnv=Canvas(master, width=400, height=400, bg='gray70')
cnv.pack(side="left")

btn=Button(text="Mélanger", command=f)
btn.pack()

lbl=Label(text="Bravo !", font=('Ubuntu', 25, 'bold'),
          justify=CENTER, width=7)
lbl.pack(side="left")

for i in range(4):
    for j in range(4):
        x, y=100*j, 100*i
        A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
        rect=cnv.create_rectangle(A, B, fill="royal blue")
        board[i][j]
        txt=cnv.create_text(C, text=board[i][j], fill="yellow",
                            font=FONT)
cnv.delete(rect)
cnv.delete(txt)
master.mainloop()

qui affiche :

• Lignes 19-20 : le label contient le message Bravo ! (option text), centré (option justify), avec une police de taille adéquate (option font). En fait, au début de la partie, le message, bien entendu, est absent et il apparaît en fin de partie. Si on ne prévoit pas l’emplacement au départ (l’option width à 7 caractères ligne 20), cela entraîne un élargissement disgrâcieux de la fenêtre.

Pour que le message apparaisse, il faut surveiller en permanence l’état du plateau board pour voir si le taquin est ordonné ou pas. Il suffit donc de définir prélablement un plateau rangé (win ci-dessous) et de le comparer à board, comme dans cet exemple artificiel :

win=[[1, 2, 3, 4],
     [5, 6, 7, 8],
     [9, 10, 11, 12],
     [13, 14, 15, 16]]

board=[[6, 7, 4, 8],
       [5, 15, 13, 2],
       [12, 14, 9, 1],
       [3, 11, 10, 16]]

print(win==board)

Cette comparaison doit se faire à chaque modification de board (donc après un clic), cf. le code ci-dessous, ligne 27. Par ailleurs, il faut à ce moment-là mettre à jour le label avec la méthode configure, cf ligne 28. En outre, il faut un drapeau (bravo, ligne 3) qui enregistre si la grille a été résolue ou pas. Voici un code partiel :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

def clic(event):
    global i_empty, j_empty, bravo
    if bravo:
        return
    i=event.y//100
    j=event.x//100
    nro=board[i][j]
    tile, txt=items[nro]
    if j+1 ==j_empty and i==i_empty:
        cnv.move(tile, 100, 0)
        cnv.move(txt, 100, 0)
    elif j-1 ==j_empty and i==i_empty:
        cnv.move(tile, -100, 0)
        cnv.move(txt, -100, 0)
    elif i+1 ==i_empty and j==j_empty:
        cnv.move(tile, 0, 100)
        cnv.move(txt, 0, 100)
    elif i-1 ==i_empty and j==j_empty:
        cnv.move(tile, 0, -100)
        cnv.move(txt, 0, -100)
    else:
        return
    board[i][j],board[i_empty][j_empty]=(
        board[i_empty][j_empty],board[i][j])
    i_empty=i
    j_empty=j
    if board==win:
        lbl.configure(text="Bravo !")
        bravo=True

def init(N=5):
    global i_empty, j_empty, items, board, bravo
    cnv.delete("all")
    items=[None]

    board=melanger(N)
    for i in range(4):
        for j in range(4):
            if board[i][j]==16:
                i_empty, j_empty=i, j

    empty=i_empty, j_empty
    normal(board, empty)
    i_empty, j_empty=3,3
    print(board)
    items=[None for i in range(17)]

    for i in range(4):
        for j in range(4):
            x, y=100*j, 100*i
            A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
            rect=cnv.create_rectangle(A, B, fill="royal blue")
            nro=board[i][j]
            txt=cnv.create_text(C, text=nro, fill="yellow",
                                font=FONT)
            items[nro]=(rect, txt)
    rect, txt=items[16]
    cnv.delete(txt)
    cnv.delete(rect)
    lbl.configure(text="")
    bravo=False


win=[[1, 2, 3, 4],
     [5, 6, 7, 8],
     [9, 10, 11, 12],
     [13, 14, 15, 16]]

La variable bravo est déclarée en variable globale dans init pour être lue dans la fonction clic et déclarée en global dans clic pour y être modifiée. Quand le jeu est mélangé, il faut penser à retirer le message de victoire (cf. ligne 26). Enfin, le drapeau bravo sert à empêcher de modifier le jeu (ligne 3) par un clic de déplacement de tuile.

cnv.bind("<Button-1>",clic)

cnv.unbind("<Button-1>")

if board==win:
    lbl.configure(text="Bravo !")
    cnv.unbind("<Button-1>")

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120

from random import randrange
from tkinter import *

def clic(event):
    global i_empty, j_empty, bravo
    if bravo:
        return
    i=event.y//100
    j=event.x//100
    nro=board[i][j]
    tile, txt=items[nro]
    if j+1 ==j_empty and i==i_empty:
        cnv.move(tile, 100, 0)
        cnv.move(txt, 100, 0)
    elif j-1 ==j_empty and i==i_empty:
        cnv.move(tile, -100, 0)
        cnv.move(txt, -100, 0)
    elif i+1 ==i_empty and j==j_empty:
        cnv.move(tile, 0, 100)
        cnv.move(txt, 0, 100)
    elif i-1 ==i_empty and j==j_empty:
        cnv.move(tile, 0, -100)
        cnv.move(txt, 0, -100)
    else:
        return
    board[i][j],board[i_empty][j_empty]=(
        board[i_empty][j_empty],board[i][j])
    i_empty=i
    j_empty=j
    if board==win:
        lbl.configure(text="Bravo !")
        bravo=True

def voisins(n, i, j):
    return [(a,b) for (a, b) in
            [(i, j+1),(i, j-1), (i-1, j), (i+1,j)]
            if a in range(n) and b in range(n)]

def echange(board, empty):
    i, j=empty
    V=voisins(4, i, j)
    ii, jj=V[randrange(len(V))]
    board[ii][jj], board[i][j]=board[i][j],board[ii][jj]
    return ii, jj

def normal(board, empty):
    i_empty, j_empty = empty
    for i in range(i_empty, 4):
        (board[i][j_empty], board[i_empty][j_empty])= (
            board[i_empty][j_empty], board[i][j_empty])
        i_empty=i
    for j in range(j_empty, 4):
        board[i_empty][j], board[i_empty][j_empty]= (
            board[i_empty][j_empty],board[i_empty][j])
        j_empty=j

def melanger(N):
    board=[[4*lin+1+col for col in range(4)]
        for lin in range(4)]

    empty=(3,3)

    for i in range(N):
        empty=echange(board, empty)
    return board

def init(N=5):
    global i_empty, j_empty, items, board, bravo
    cnv.delete("all")
    items=[None]


    board=melanger(N)
    for i in range(4):
        for j in range(4):
            if board[i][j]==16:
                i_empty, j_empty=i, j

    empty=i_empty, j_empty
    normal(board, empty)
    i_empty, j_empty=3,3
    print(board)
    items=[None for i in range(17)]

    for i in range(4):
        for j in range(4):
            x, y=100*j, 100*i
            A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
            rect=cnv.create_rectangle(A, B, fill="royal blue")
            nro=board[i][j]
            txt=cnv.create_text(C, text=nro, fill="yellow",
                                font=FONT)
            items[nro]=(rect, txt)
    rect, txt=items[16]
    cnv.delete(txt)
    cnv.delete(rect)
    lbl.configure(text="")
    bravo=False

FONT=('Ubuntu', 27, 'bold')
master=Tk()
cnv=Canvas(master, width=400, height=400, bg='gray70')
cnv.pack(side='left')

btn=Button(text="Mélanger", command=init)
btn.pack()

lbl=Label(text="      ", font=('Ubuntu', 25, 'bold'),
          justify=CENTER, width=7)
lbl.pack(side="left")

cnv.bind("<Button-1>",clic)
init()

win=[[1, 2, 3, 4],
     [5, 6, 7, 8],
     [9, 10, 11, 12],
     [13, 14, 15, 16]]

master.mainloop()

Alternative de mélange¶

On peut simplifier la génération d’un mélange du plateau de la manière suivante :

• on part de la liste ordonnée de tous les numéros de 1 à 15,
• on effectue un nombre pair d’échanges de deux numéros
• on place le mélange obtenu dans une grille, ligne par ligne
• on termine la grille en rajoutant la tuile 16.

Le programme ci-dessous génère une grille valide conformément à la méthode ci-dessus :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

from random import randrange

def echange(L):
    i,j = randrange(15),randrange(15)
    L[i], L[j]=L[j], L[i]

def melanger(N=10):
    L=list(range(1,16))

    for i in range(2*N):
        echange(L)
    L.append(16)
    return [[L[4*i+j] for j in range(4)] for i in range(4)]

board=melanger()

print(*board, sep='\n')

18
19
20
21

[10, 4, 9, 14]
[5, 1, 2, 11]
[8, 7, 6, 12]
[15, 13, 3, 16]

En fait, si on génère aléatoirement une permutation des entiers de 1 à 15, on a une chance sur 2 que cette permutation soit résoluble ; le caractère résoluble de la permutation peut se déterminer facilement par un calcul de signature de permutation.

Alternative de codage du déplacement de tuile¶

Dans le code précédent taquin_sequentiel.py de codage du déplacement d’une tuile :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def clic(event):
    global i_empty, j_empty
    i=event.y//100
    j=event.x//100
    nro=board[i][j]
    rect, txt=items[nro]
    if j+1 ==j_empty and i==i_empty:
        cnv.move(rect, 100, 0)
        cnv.move(txt, 100, 0)
    elif j-1 ==j_empty and i==i_empty:
        cnv.move(rect, -100, 0)
        cnv.move(txt, -100, 0)
    elif i+1 ==i_empty and j==j_empty:
        cnv.move(rect, 0, 100)
        cnv.move(txt, 0, 100)
    elif i-1 ==i_empty and j==j_empty:
        cnv.move(rect, 0, -100)
        cnv.move(txt, 0, -100)
    else:
        return
    board[i][j],board[i_empty][j_empty]=(
        board[i_empty][j_empty],board[i][j])
    i_empty=i
    j_empty=j

il y a beaucoup de redondance de code parce qu’on examine les 4 cas les uns après les autres et que ces cas se traitent de manière analogue. En réalité, au prix (peut-être) d’une moins grande facilité de compréhension, il est possible de réduire au minimum le traitement individuel de chaque cas. Il suffit essentiellement de produire un vecteur de déplacement valable dans tous les cas. C’est basé sur le principe qu’un vecteur se comprend comme « extrémité moins origine » (lignes 10-11 ci-dessous), comme le montre le code suivant :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

def clic(event):
    global i_empty, j_empty
    i=event.y//100
    j=event.x//100
    empty_around=(i_empty in [i-1, i+1] and j==j_empty
                  or j_empty in [j-1, j+1] and i==i_empty)
    if empty_around:
        nro=board[i][j]
        tile, txt=items[nro]
        move_x=(j_empty-j)*100
        move_y=(i_empty-i)*100
        cnv.move(tile, move_x, move_y)
        cnv.move(txt, move_x, move_y)
        board[i][j],board[i_empty][j_empty]=(
            board[i_empty][j_empty],board[i][j])
        i_empty=i
        j_empty=j

• Lignes 5-6 : la fonction clic commence par déterminer si oui ou non, autour du clic se trouve la case vide ; c’est le booléen empty_around qui enregistre cet état. Le code commence d’abord par regarder si la case vide serait au-dessus (i_empty == i-1) ou au-dessous (i_empty == i+1) ; ensuite, il est examiné si la case vide est à gauche ou à droite. C’est la seule partie du code qui fait du cas par cas.
• Ligne 7 : si empty_around vaut False, c’est que soit on a cliqué sur la case vide soit, au contraire, qu’on a cliqué sur une tuile « bloquée ». Dans ce cas, aucun mouvement n’a lieu et l’exécution quitte la fonction clic.
• Comme dans le code précédent, on peut identifier (lignes 8-9) la tuile, son numéro et ses id.
• Pour rechercher le vecteur de déplacement (move_x, move_y) de la tuile, grâce à une astuce de calcul, on peut s’éviter de considérer les quatre cas. L’idée de base est qu’un vecteur se mesure par la formule « extrémité moins origine », ici plutôt « destination moins origine », cf. lignes 10-11. Comme le vecteur est en pixels, il faut multiplier par 100, la taille de chaque tuile.
• Comme dans le code précédent, on échange la case vide et la tuile déplacée (lignes 14-15) et on met à jour la case vide (lignes 16-17).

Voici le code complet :

taquin_sequentiel_plus.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

from random import randrange
from tkinter import *

def clic(event):
    global i_empty, j_empty
    i=event.y//100
    j=event.x//100
    empty_around=(i_empty in [i-1, i+1] and j==j_empty
                  or j_empty in [j-1, j+1] and i==i_empty)
    if empty_around:
        nro=board[i][j]
        tile, txt=items[nro]
        move_x=(j_empty-j)*100
        move_y=(i_empty-i)*100
        cnv.move(tile, move_x, move_y)
        cnv.move(txt, move_x, move_y)
        board[i][j],board[i_empty][j_empty]=(
            board[i_empty][j_empty],board[i][j])
        i_empty=i
        j_empty=j

items=[None for i in range(17)]
board=[[6, 7, 4, 8],
       [5, 15, 13, 2],
       [12, 14, 9, 1],
       [3, 11, 10, 16]]

FONT=('Ubuntu', 27, 'bold')
master=Tk()
cnv=Canvas(master, width=400, height=400, bg='gray70')
cnv.pack(side='left')

i_empty, j_empty=3,3

for i in range(4):
    for j in range(4):
        x, y=100*j, 100*i
        A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
        rect=cnv.create_rectangle(A, B, fill="royal blue")
        nro=board[i][j]
        txt=cnv.create_text(C, text=nro, fill="yellow",
                            font=FONT)
        items[nro]=(rect, txt)

cnv.delete(txt)
cnv.delete(rect)

cnv.bind("<Button-1>",clic)

master.mainloop()

Déplacement progressif des tuiles¶

Dans notre taquin séquentiel actuel, la méthode move du canevas fait un déplacement instantané d’un item du canevas. Pour obtenir un effet de fluidité, on souhaiterait un déplacement progressif de chaque tuile.

La technique employée pour changer une tuile de position est la suivante. On va déplacer la tuile

• d’une certaine distance, petite, par exemple DIST = 10 pixels,
• à intervalles réguliers, par exemple DELTA = 20 millisecondes,

ce qui donnera un effet d’animation. La répétition sera assurée par l’utilisation de la méthode after.

Lorsqu’on doit déplacer une tuile, on peut assez facilement déterminer la direction de déplacement sous la forme d’un vecteur « unitaire » (x,y), où x représente une ligne, y représente une colonne et où x et y valent \(\mathtt{-1, 1}\) ou \(\mathtt{0}\); par exemple un vecteur valant (0, -1) désignera un déplacement de la tuile vers le haut. On connaît par ailleurs la position initiale et la position finale de la tuile (dans la case vide).

Voici la fonction d’animation :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

DELTA=20
DIST=10

def anim(item, target, drtn):
    L =cnv.coords(item)
    a=L[0]
    b=L[1]
    x, y=target
    u, v=drtn
    if u*(x-a)+v*(y-b)>DIST:
        cnv.move(item, u*DIST, v*DIST)
        cnv.after(DELTA, anim, item, target, drtn)
    else:
        cnv.move(item, (x-a), (y-b))

On remarquera que cette fonction d’animation traite génériquement d’un déplacement horizontal (droite ou gauche) et d’un déplacement vertical (haut ou bas), aucun cas n’est explicitement distingué. La fonction anim reçoit l’id de l’item à déplacer (item), la position finale de l’item (target) et la direction drtn de déplacement sous la forme (x, y) où x et y valent \(\mathtt{0}\), \(\mathtt{-1}\) ou \(\mathtt{1}\).

On commence par récupérer les coordonnées (a, b) d’un élément de l’item grâce à la méthode coords du canevas. Pour un rectangle, cet élément sera le coin supérieur gauche. Pour du texte, ce sera le centre du texte. Ensuite on regarde la distance que l’item doit encore à parcourir avant destination ; cette distance vaut u*(x-a)+v*(y-b), ce qui est encore une variante du raccourci « vecteur = extrémité - origine ». Si cette distance est inférieure à un écart DIST (lignes 10) qu’on s’est donné au départ (ligne 2), on déplace l’item avec la méthode move de cette distance suivant la direction drtn cf. ligne 9). Sinon (lignes 13-14), c’est qu’on est très proche de la position définitive et on place l’item à sa position finale (à nouveau, « vecteur = extrémité - origine »)

La fonction anim est appelée à la place des appels que l’on faisait à la méthode clic dans la fonction de déplacement de tuile du taquin séquentiel. On connaît les items à déplacer : un rectangle et du texte. Le coin supérieur gauche de la tuile, représenté par board[i][j], a pour coordonnées sur le canevas

a = j * 100
b = i * 100

puisque 100 est la dimension de chaque tuile. Le centre de la tuile a pour coordonnées

j * 100 + 50
i * 100 + 50

Pour la suite, on se base sur le code taquin_sequentiel_plus.py. Voici le nouveau code de la fonction clic :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

def clic(event):
    global i_empty, j_empty
    i=event.y//100
    j=event.x//100

    empty_around=(i_empty in [i-1, i+1] and j==j_empty
                  or j_empty in [j-1, j+1] and i==i_empty)
    if empty_around:
        nro=board[i][j]
        rect, txt=items[nro]

        target=100*j_empty, 100*i_empty
        drtn=j_empty -j, i_empty-i
        target_txt=100*j_empty+50, 100*i_empty+50

        anim(rect, target, drtn)
        anim(txt, target_txt, drtn)

        board[i][j],board[i_empty][j_empty]=(board[i_empty][j_empty],
                                             board[i][j])
        i_empty=i
        j_empty=j

• On détermine la position finale sur le canevas du coin supérieur gauche du rectangle (target, ligne 12) et du texte (target_txt, ligne 14)
• On determine la direction unitaire de déplacement, cf. ligne 13. Et on appelle la fonction d’animation anim (lignes 16-17).

D’où le code complet suivant :

taquin_progressif_simple.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

from random import randrange
from tkinter import *

DELTA=20
DIST=10

def anim(item, target, drtn):
    L =cnv.coords(item)
    a=L[0]
    b=L[1]
    x, y=target
    u, v=drtn
    if u*(x-a)+v*(y-b)>DIST:
        cnv.move(item, u*DIST, v*DIST)
        cnv.after(DELTA, anim, item, target, drtn)
    else:
        cnv.move(item, (x-a), (y-b))

def clic(event):
    global i_empty, j_empty
    i=event.y//100
    j=event.x//100

    empty_around=(i_empty in [i-1, i+1] and j==j_empty
                  or j_empty in [j-1, j+1] and i==i_empty)
    if empty_around:
        nro=board[i][j]
        rect, txt=items[nro]

        target=100*j_empty, 100*i_empty
        drtn=j_empty -j, i_empty-i
        target_txt=100*j_empty+50, 100*i_empty+50

        anim(rect, target, drtn)
        anim(txt, target_txt, drtn)

        board[i][j],board[i_empty][j_empty]=(board[i_empty][j_empty],
                                             board[i][j])
        i_empty=i
        j_empty=j

items=[None for i in range(17)]
board=[[6, 7, 4, 8],
       [5, 15, 13, 2],
       [12, 14, 9, 1],
       [3, 11, 10, 16]]

FONT=('Ubuntu', 27, 'bold')
master=Tk()
cnv=Canvas(master, width=400, height=400, bg='gray70')
cnv.pack()

i_empty, j_empty=3,3

for i in range(4):
    for j in range(4):
        x, y=100*j, 100*i
        A, B, C=(x, y), (x+100, y+100), (x+50, y+50)
        rect=cnv.create_rectangle(A, B, fill="royal blue")
        nro=board[i][j]
        txt=cnv.create_text(C, text=nro, fill="yellow",
                            font=FONT)
        items[nro]=(rect, txt)

cnv.delete(txt)
cnv.delete(rect)

cnv.bind("<Button-1>",clic)

master.mainloop()