Présentation de la fourmi de Langton¶

Dans cette activité, on présente un automate cellulaire créé en 1986 par Christopher Langton, pionnier de la vie artificielle. On dispose d’un quadrillage et initialement, une fourmi est placée sur une case. Tel un automate, la fourmi va alors effectuer une suite de mouvements suivant des cases adjacentes et variant selon la couleur de la case (claire ou foncée, cf. les règles ci-dessous). Au départ, les cases sont de couleur claire. À tout moment, la fourmi est à une certaine position et possède une certaine direction de déplacement (la flèche rouge sur les dessins). Dans ce qui suit, on suppose que la fourmi est sur une case A. Les mouvements sont définis par les 3 règles suivantes :

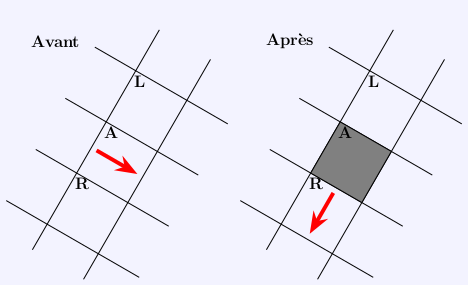
• si la fourmi est sur une case claire, elle se déplace dans la case qui est à sa droite (R sur le dessin) :

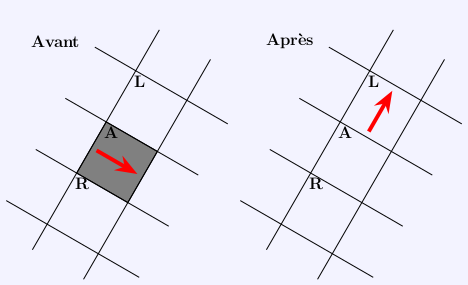
• si la fourmi est sur une case sombre, elle se déplace dans la case qui est à sa gauche (L sur le dessin) :

• chaque fois que la fourmi se déplace de la case A à une case voisine, la couleur de la case A change :

  • A devient sombre si A était claire
  • A devient claire si A était sombre.

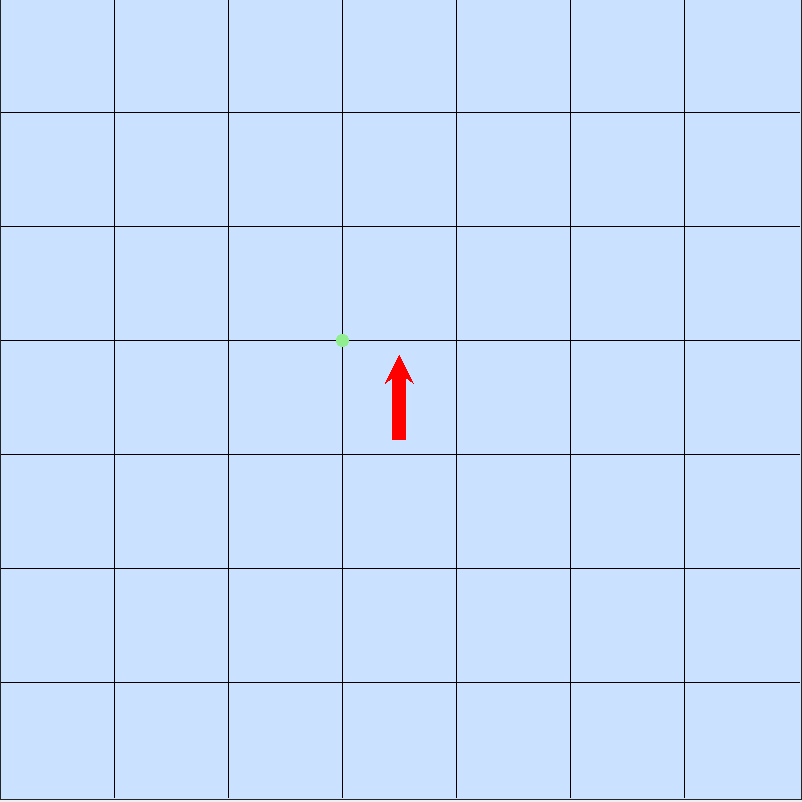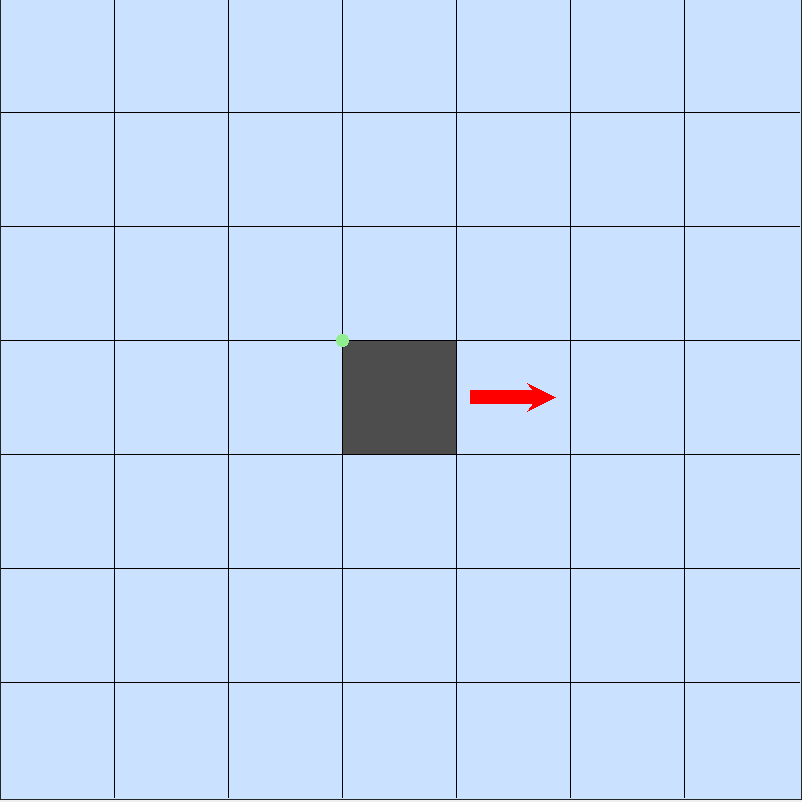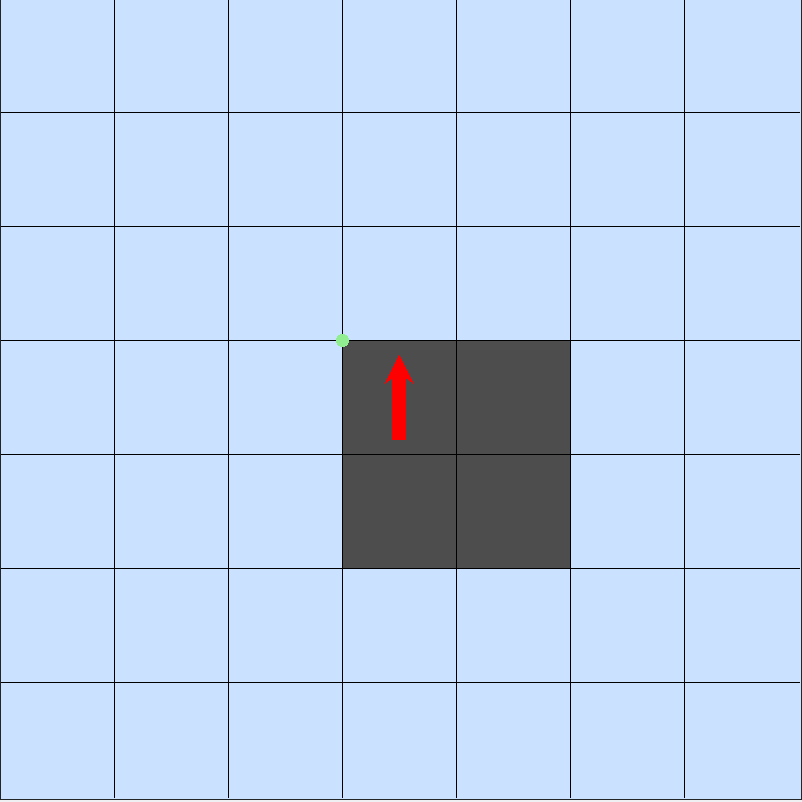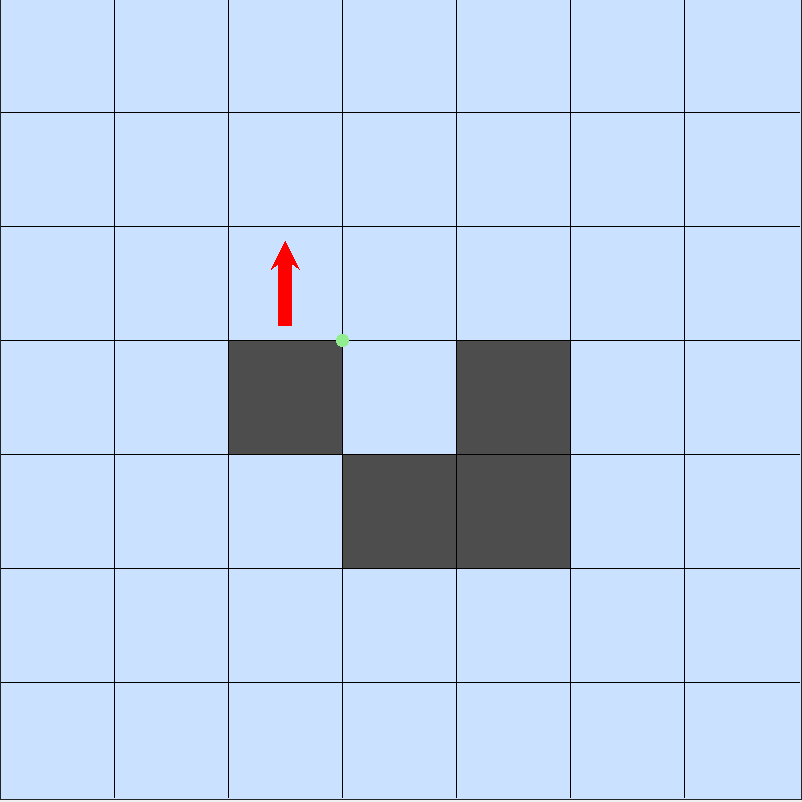
Au départ, la fourmi est tournée vers le nord et est placée sur une case claire. L’expérience consiste à analyser l’allure globale des déplacements de la fourmi.

Voici, en images, les 7 premiers états de la fourmi (le point vert indique le départ) :

Ce qui rend la fourmi de Langton extraordinaire, c’est que si on la laisse évoluer, on observe successivement les phénomènes suivants :

• construction de motifs symétriques noirs jusque, environ, le 500e mouvement ;
• comportement moins ordonné jusque environ le 10000e mouvement ;
• stabilisation indéfinie du mouvement en un déplacement rectiligne sur une « autoroute » !!

L’animation ci-dessous montre ce comportement.

Présentation de l’activité¶

L’activité est assez courte et abordable, au moins dans sa première partie. La 2e partie nécessite les mêmes connaissances mais est légèrement plus complexe, c’est un approfondissement. Concernant le langage Python, il est souhaitable

• d’avoir quelques mois de pratique (sans doute essentiel)
• d’avoir compris la logique du découpage en fonctions (capital)
• de connaître les conditions if/elif/else
• d’avoir compris l’usage du déclateur global
• d’avoir utilisé des listes de listes
• d’avoir rencontré des listes en compréhension emboîtées (mais ce n’est pas rédhibitoire, on peut contourner ce point).

Pour Tkinter, il faut

• avoir intégré qu’une réalisation graphique se crée (souvent) en interprétant un modèle (ici une liste 2D)
• savoir créer une fenêtre et un widget
• avoir compris la notion d’id d’un item,
• connaître la méthode delete sur un item
• savoir dessiner des rectangles et des lignes sur le canevas
• savoir créer une animation avec la méthode after.

Version basique¶

La fourmi va évoluer sur un quadrillage carré. La largeur totale du quadrillage sera, par exemple, de SIDE = 1000 pixels. On fixera le nombre de lignes ou de colonnes du quadrillage à DIM=100 par exemple. Le côté de chaque case vaudra donc UNIT = SIDE // DIM pixels. En outre, on définira les couleurs COLOR_ON (sombre) et COLOR_OFF (claire). D’où les déclarations suivantes :

from tkinter import *

SIDE = 1000
WIDTH = SIDE
HEIGHT = SIDE
DIM=100
UNIT = SIDE // DIM
COLOR_ON = 'gray30'
COLOR_OFF = 'LightSteelBlue1'

La fourmi se déplace dans un tableau 2D nommé items, ayant DIM lignes et DIM colonnes. La position courante de la fourmi est répertoriée par un couple d’indices (i, j) où i est l’indice de ligne et j l’indice de colonne. Il faut penser le tableau items comme un quadrillage. Quand je parle de case (i, j), il s’agit toujours d’une position ligne x colonne dans le tableau. Par rapport au canevas Tkinter, la case (i, j) du quadrillage est la case dont le coin supérieur gauche est de coordonnées (x, y) suivantes :

x = j * UNITS
y = i * UNITS

(on notera l’inversion de l’ordre : j pour x et i pour y).

Pour déplacer la fourmi à un instant donné, il faut disposer de

• de sa case de position à cet instant,
• de sa direction courante,
• des couleurs des cases du quadrillage.

Dans le code, la position courante de la fourmi sera enregistrée dans une variable globale pos = (i, j). Sa direction courante sera placée dans la variable globale drn. Cette direction prendra 4 valeurs donnée par les quatre points cardinaux, représentés par les caractères "N", "S", "E" et "W".

Le quadrillage ne sera pas dessiné. Au départ, toutes les cases ont la couleur de fond du canevas. Le tableau items est rempli alors de 0. Pour transformer une case (i, j) claire en une case sombre, on dessinera sous Tkinter un carré sombre sur la case claire. Le carré sombre qui est dessiné est un item du canevas, créé avec la méthode create_rectangle. Lorsqu’il est créé, l’id du rectangle dessiné sera placé à la position (i, j) du tableau items. On remarquera que cet id ne peut être nulle (une id du canevas commence toujours à partir de l’entier 1). A l’inverse, pour transformer une case sombre (i, j) en une case claire, on supprimera avec la méthode delete le rectangle noir dessiné sur la case et on passera à 0 la valeur de items[i][j]. Ainsi, items[i][j sera toujours le reflet du plateau dessiné sur le canevas.

Comment dessiner la position suivante de la position courante de la fourmi ? Pour cela, on dispose de la position courante pos = (i, j) et de la direction courante drn. En allant regarder dans items[i][j] on va obtenir la couleur de la case courante. A partir de là, on peut calculer la position suivante. Par exemple, si i=42, j=81 , dir="W" et la case (i, j) est noire alors la fourmi se déplace à sa gauche (donc vers la bas), donc sa nouvelle position est (42, 82) et sa nouvelle direction est "S".

Écrivons donc le code d’une fonction bouger qui renvoie la nouvelle position et la nouvelle direction :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

def bouger(pos, drn, items):
    i, j = pos

    if items[i][j] == 0:
        if drn == "N":
            r = (i, j + 1), "E"
        elif drn == "S":
            r = (i, j - 1), "W"
        elif drn == "E":
            r = (i + 1, j), "S"
        elif drn == "W":
            r = (i - 1, j), "N"
    else:
        if drn == "S":
            r = (i, j + 1), "E"
        elif drn == "N":
            r = (i, j - 1), "W"
        elif drn == "W":
            r = (i + 1, j), "S"
        elif drn == "E":
            r = (i - 1, j), "N"
    return r

• Noter que la fonction est indépendante de Tkinter.
• Ligne 1 : la fonction suppose connues la position courante, la direction courante et les couleurs des cases (tableau items).
• Ligne 22 : la fonction renvoie r qui est un couple (npos, ndrn) où npos est la nouvelle position sous forme d’un couple ligne x colonne et où ndrn est la nouvelle direction (donc parmi "N", "S", "E" et "W").
• Lignes 4 et 13 : il y a essentiellement deux cas selon la couleur de la case courante. Si item[i][j]==0 c’est que la couleur courante est la couleur de fond (couleur claire).
• Lignes 18-19 : par exemple, si la couleur de la case (i, j) est sombre et si la direction est W alors la fourmi se déplace vers le sud et sa nouvelle position est (i+1, j) (une ligne en dessous et la même colonne).

Une fois la nouvelle position calculée, il faut juste changer la couleur de la case courante en clair, dans l’exemple (42, 81), donc effacer l’item du canevas répertorié à items[42][81] et réaffecter items[42][81] = 0 pour mémoriser la couleur claire.

Ecrivons maintenant la fonction qui change la couleur de la case courante :

1
2
3
4
5
6

def draw_square(i, j):
    x, y = j * UNIT, i * UNIT
    square = cnv.create_rectangle((x, y), (x + UNIT, y + UNIT),
                                  fill=COLOR_ON,
                                  outline='')
    return square

• Ligne 1 : la fonction reçoit une position (i, j), en principe, qui aura été lue au préalable dans la grille items.
• Ligne 3 : la fonction dessine un carré sombre (COLOR_ON) à la position du canevas représentant la case (i, j).
• Ligne 2 : noter l’inversion de i et j par rapport à x et y.
• ligne 5 : c’est un détail, mais on retire le bord du rectangle pour que le carré soit net.
• Ligne 6 : la fonction renvoie l’id du carré dessiné (sinon, il serait impossible de l’effacer par la suite).

Ecrivons la fonction de dessin des cases :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def draw(pos, drn, items):
    (ii, jj), ndrn = bouger(pos, drn, items)
    i, j = pos
    square = items[i][j]

    if square == 0:
        square = draw_square(i, j)
        items[i][j] = square
    else:
        cnv.delete(square)
        items[i][j] = 0

    return (ii, jj), ndrn

• Ligne 1 : la fonction dispose de la position, de la direction courantes et un accès aux items.
• Ligne 13 : la fonction retourne la nouvelle position et la nouvelle direction après avoir modifié le plateau Tkinter (lignes 8 et 11)
• Lignes 6-7 : si la case courante est claire, un carré sombre est dessiné.
• Ligne 9-10 : si la case courante est foncée, le carré sombre est supprimé.

def anim():
    global pos, drn
    pos, drn = draw(pos, drn)
    root.after(DELAY, anim)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

from tkinter import *

SIDE = 1000
WIDTH = SIDE
HEIGHT = SIDE
DIM = 95
UNIT = SIDE // DIM
DELAY = 1
COLOR_ON = 'gray30'
COLOR_OFF = 'LightSteelBlue1'


def draw_square(i, j):
    x, y = j * UNIT, i * UNIT
    square = cnv.create_rectangle((x, y), (x + UNIT, y + UNIT),
                                  fill=COLOR_ON,
                                  outline='')
    return square


def draw(pos, drn, items):
    (ii, jj), ndrn = bouger(pos, drn, items)
    i, j = pos
    square = items[i][j]

    if square == 0:
        square = draw_square(i, j)
        items[i][j] = square
    else:
        cnv.delete(square)
        items[i][j] = 0

    return (ii, jj), ndrn


def bouger(pos, drn, items):
    i, j = pos

    if items[i][j] == 0:
        if drn == "N":
            r = (i, j + 1), "E"
        elif drn == "S":
            r = (i, j - 1), "W"
        elif drn == "E":
            r = (i + 1, j), "S"
        elif drn == "W":
            r = (i - 1, j), "N"
    else:
        if drn == "S":
            r = (i, j + 1), "E"
        elif drn == "N":
            r = (i, j - 1), "W"
        elif drn == "W":
            r = (i + 1, j), "S"
        elif drn == "E":
            r = (i - 1, j), "N"
    return r


def anim():
    global pos, drn
    pos, drn = draw(pos, drn, items)
    root.after(DELAY, anim)


root = Tk()
cnv = Canvas(root, width=WIDTH, height=HEIGHT, background=COLOR_OFF)
cnv.pack(side=LEFT)

nwidth = WIDTH // UNIT
nheight = HEIGHT // UNIT

items = [[0] * nwidth for _ in range(nheight)]
pos = (nheight // 2-10, nwidth // 2+19)
drn = "N"
anim()
print(DIM, nwidth, nheight)

root.mainloop()

Simplification du code de la fonction bouger¶

La fonction bouger permet de déterminer le nouvel état de la fourmi en fonction de l’ancien. Le code était :

def bouger(pos, drn, items):
    i, j = pos

    if items[i][j] == 0:
        if drn == "N":
            r = (i, j + 1), "E"
        elif drn == "S":
            r = (i, j - 1), "W"
        elif drn == "E":
            r = (i + 1, j), "S"
        elif drn == "W":
            r = (i - 1, j), "N"
    else:
        if drn == "S":
            r = (i, j + 1), "E"
        elif drn == "N":
            r = (i, j - 1), "W"
        elif drn == "W":
            r = (i + 1, j), "S"
        elif drn == "E":
            r = (i - 1, j), "N"
    return r

Il est possible de le simplifier largement. Pour désigner les directions, il est plus commode d’utiliser des entiers que de simples lettres. Plus précisément, la direction sera indiquée par le mouvement ligne x colonne dans la grille. Par exemple, pour aller vers le nord, la direction sera (-1, 0) : en effet, il y a une ligne de moins (d’où - 1) et la colonne est la même (d’où 0). L’intérêt de procéder ainsi est que la nouvelle position s’obtient en faisant une addition de vecteurs ; par exemple, si la fourmi est en (i, j) et que la nouvelle direction est (aa, bb) la nouvelle position est (i + aa, j + bb).

Reste à savoir comment calculer la nouvelle direction en fonction de l’ancienne. La nouvelle position dépend de la couleur de la case courante. Quelques essais montrent que si la direction est (a, b) alors :

• si la case est claire, la nouvelle direction est (b, -a) ;
• si la case est sombre, la nouvelle direction est (-b, a)

(mathématiquement, ce sont, à un facteur près, des rotations de quart de tour, direct ou indirect).

Par exemple, si la case est claire et que la direction est (a, b) = (1, 0) (donc, le sud) alors la nouvelle direction est l’ouest, donc (bb, -aa) = (0, -1).

On peut donc récrire le code de la fonction bouger plus simplement :

bouger_alt.py

def bouger(pos, drn, items):
    i, j = pos
    a, b = drn
    aa, bb = (b, -a) if items[i][j] == 0 else (-b, a)
    return (i + aa, j + bb), (aa, bb)

Dessiner et contrôler la fourmi¶

On va modifier le code pour obtenir une animation contrôlable :

La fourmi sera représentée par une flèche rouge qui indiquera sa direction de déplacement. En outre, il sera possible d’arrêter ou de reprendre le déplacement de la fourmi en appuyant sur la barre d’espace. Enfin, on pourra réinitialiser le plateau en appuyant sur la touche Echap.

Il faut déjà dessiner la grille. Rien de difficile, il suffit de tracer des lignes avec create_line :

grille.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

from tkinter import *

SIDE = 400
WIDTH = SIDE
HEIGHT = SIDE
DIM = 4
UNIT = SIDE // DIM
COLOR_OFF = 'LightSteelBlue1'

def make_grid():
    for j in range(nwidth):
        cnv.create_line((j * UNIT, 0), (j * UNIT, HEIGHT))
    for i in range(nheight):
        cnv.create_line((0, i * UNIT), (WIDTH, i * UNIT))


root = Tk()
cnv = Canvas(root, width=WIDTH, height=HEIGHT,
             background=COLOR_OFF)
cnv.pack()

nwidth = WIDTH // UNIT
nheight = HEIGHT // UNIT

make_grid()

root.mainloop()

• Lignes 11 et 13 : on détermine le nombre de colonnes et le nombre de lignes de la grille (lignes 22-23) et on trace sur le canevas autant de traits horizontaux et verticaux.
• La case dans la grille de position ligne x colonne (i, j) est représentée par un carré de côté de longueur UNIT et identifiée par son coin supérieur gauche de coordonnées (j * UNITS, i * UNIT) sur le canevas Tkinter.

Il faut ensuite savoir représenter une flèche dans une case. Pour fixer les idées, plaçons une flèche comme dans la grille ci-dessous aux deux cases (i, j) = (2, 1) et (i, j) = (1, 3) :

Pour cela, on fait comme si on dessinait chaque flèche dans la case (0, 0) puis on la tranlate à la case (i, j) en rajoutant, à un facteur près, i et j aux coordonnées des extrémités de la flèche.

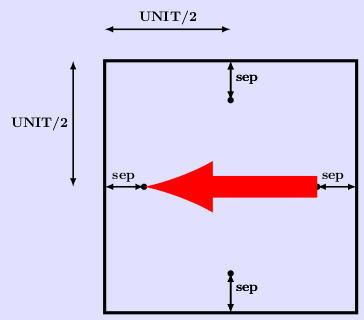
Plus précisément, on se donne une petite distance (disons sep) et on place les quatre points cardinaux, bien centrés dans la case et chacun à une distance sep du bord de la case :

Pour tracer une flèche, il suffira de tracer une ligne avec la méthode create_line et l’option arrow entre les deux point cardinaux représentant l’origine et l’extrémité de la flèche (sur le dessin, on relie est à ouest). D’où le code suivant :

fleche.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

from tkinter import *

SIDE = 400
WIDTH = SIDE
HEIGHT = SIDE
DIM = 4
UNIT = SIDE // DIM
COLOR_OFF = 'LightSteelBlue1'

ARROW_WIDTH = UNIT // 8

def make_grid():
    for i in range(nwidth):
        cnv.create_line((i * UNIT, 0), (i * UNIT, HEIGHT))
    for i in range(nheight):
        cnv.create_line((0, i * UNIT), (WIDTH, i * UNIT))

def draw_arrow(i, j, drn):
    sep = UNIT // 8
    east = (sep, UNIT // 2)
    west = (UNIT - sep, UNIT // 2)
    north = (UNIT // 2, sep)
    south = (UNIT // 2, UNIT - sep)
    x, y = j * UNIT, i * UNIT
    if drn == (0, 1):
        A = (x + east[0], y + east[1])
        B = (x + west[0], y + west[1])
    elif drn ==  (-1, 0):
        A = (x + south[0], y + south[1])
        B = (x + north[0], y + north[1])
    elif drn ==  (0, -1):
        B = (x + east[0], y + east[1])
        A = (x + west[0], y + west[1])
    else:
        B = (x + south[0], y + south[1])
        A = (x + north[0], y + north[1])
    return cnv.create_line(
        A,
        B,
        width=ARROW_WIDTH,
        arrow='last',
        fill='red',
        arrowshape=(18, 30, 8))


root = Tk()
cnv = Canvas(root, width=WIDTH, height=HEIGHT,
             background=COLOR_OFF)
cnv.pack()

nwidth = WIDTH // UNIT
nheight = HEIGHT // UNIT

make_grid()
draw_arrow(2, 1, (0, -1))
draw_arrow(1, 3, (-1, 0))

root.mainloop()

• Ligne 19 : La séparation sep est calculée en fonction de la taille de la case.
• Lignes 20-22 : On référence les quatre points cardinaux dans la case en position (0, 0). Pour centrer, on utilise UNIT/∕2.
• Ligne 24 : (x, y) représente les coordonnées sur le canevas Tkinter du coin supérieur droit de la case en position ligne x colonne (i, j).
• Lignes 32-33 et analogues : pour dessiner une flèche (ici vers l’ouest) dans la case (i, j), on définit ses extrémités \(\mathtt{A}\) et \(\mathtt{B}\) (donc A est à l’ouest et B est à l’est), et on calcule les coordonnées de ces points. Il suffit pour cela de décaler du vecteur (j*UNITS, i*UNITS) une flèche identique mais tracée dans la case (0,0).

Lors de l’animation, à chaque nouvelle position de la fourmi, on supprime la flèche correspondant à la position courante et on dessine, avec la fonction ci-dessus, la flèche pour la nouvelle position. D’où le code suivant :

demo.py

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106

from tkinter import *

SIDE = 600
WIDTH = SIDE
HEIGHT = SIDE
UNIT = SIDE // 7
ARROW_WIDTH = UNIT // 8
DELAY = 500

COLOR_GRID = "black"
COLOR_ON = 'gray30'
COLOR_OFF = 'LightSteelBlue1'

def draw_arrow(i, j, drn):
    sep = UNIT // 8
    east = (sep, UNIT // 2)
    west = (UNIT - sep, UNIT // 2)
    north = (UNIT // 2, sep)
    south = (UNIT // 2, UNIT - sep)
    x, y = j * UNIT, i * UNIT
    if drn == (0, 1):
        A = (x + east[0], y + east[1])
        B = (x + west[0], y + west[1])
    elif drn ==  (-1, 0):
        A = (x + south[0], y + south[1])
        B = (x + north[0], y + north[1])
    elif drn ==  (0, -1):
        B = (x + east[0], y + east[1])
        A = (x + west[0], y + west[1])
    else:
        B = (x + south[0], y + south[1])
        A = (x + north[0], y + north[1])
    return cnv.create_line(
        A,
        B,
        width=ARROW_WIDTH,
        arrow='last',
        fill='red',
        arrowshape=(18, 30, 8))


def draw_square(i, j):
    x, y = j * UNIT, i * UNIT
    square = cnv.create_rectangle((x, y), (x + UNIT, y + UNIT),
                                  fill=COLOR_ON,
                                  outline='')
    cnv.tag_lower(square)
    return square


def draw(pos, drn, arrow, items):
    cnv.delete(arrow)
    (ii, jj), ndrn = bouger(pos, drn, items)
    i, j = pos
    square = items[i][j]

    if square == 0:
        square = draw_square(i, j)
        items[i][j] = square
    else:
        cnv.delete(square)
        items[i][j] = 0

    narrow = draw_arrow(ii, jj, ndrn)
    return (ii, jj), ndrn, narrow

def bouger(pos, drn, items):
    i, j = pos
    a, b = drn
    aa, bb = (b, -a) if items[i][j] == 0 else (-b, a)
    return (i + aa, j + bb), (aa, bb)

def anim():
    global pos, drn, arr
    pos, drn, arr = draw(pos, drn, arr, items)
    id_anim = cnv.after(DELAY, anim)


root = Tk()
cnv = Canvas(root, width=WIDTH, height=HEIGHT, background=COLOR_OFF)
cnv.pack(side=LEFT)

nwidth = WIDTH // UNIT
nheight = HEIGHT // UNIT


def make_grid():
    for i in range(nwidth):
        cnv.create_line((i * UNIT, 0), (i * UNIT, HEIGHT), fill=COLOR_GRID)
    for i in range(nheight):
        cnv.create_line((0, i * UNIT), (WIDTH, i * UNIT), fill=COLOR_GRID)


def init():
    global items, pos, drn, arr
    make_grid()

    items = [[0] * nwidth for _ in range(nheight)]
    pos = (nheight // 2, nwidth // 2)
    drn = (1, 0)
    arr = draw_arrow(pos[0], pos[1], drn)
    anim()


init()
root.mainloop()

Le code est basé sur anim.py et bouger_alt.py. Voici quelques explications spécifiques :

• Ligne 95 : l’écriture d’une fonction init (ligne 94) oblige à déclarer certaines variables global.
• Ligne 74 : à chaque étape de l’animation, la position pos, la direction drn, la flèche arr sont mises à jour, d’où la nécessité de les déclarer en global. La variable items n’est pas réaffectée et est déjà globale (cf. ligne 95).
• Ligne 51 : la fonction draw a été modifiée pour renvoyer aussi l’id de la flèche afin qu’elle puisse être effacée ultérieurement.
• Ligne 47 : la grille est dessinée la première (ligne 96). Ensuite, des cases sombres sont dessinées suivant les déplacements de la fourmi. Le bord des cases sombres va donc cacher des parties de la grille. Il faut donc faire passer au dernier plan ces cases sombres : c’est le rôle de la méthode tag_lower.

Pour finir, on va permettre de contrôler au clavier la progression de la fourmi : un appui sur la barre d’espace mettra en pause son déplacement et un nouvel appui relancera. On va aussi permettre de reprendre l’animation depuis le début en appuyant sur la touche Echap au lieu de devoir fermer et relancer l’application.

Pour cela, on utilise un drapeau stop qui indique si l’animation est arrêtée ou pas. L’animation tourne indéfiniment (cf.ligne 77 ci-dessous). Lorsqu’on remet à zéro l’animation, il faut désactiver l’animation courante. Pour cela, on mémorise l’id de l’animation en cours et grâce à la méthode after_cancel on pourra la désactiver.

D’où le code suivant :

demo_stop.py

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125

from tkinter import *

SIDE = 600
WIDTH = SIDE
HEIGHT = SIDE
UNIT = SIDE // 7
ARROW_WIDTH = UNIT // 8
DELAY = 500

COLOR_GRID = "black"
COLOR_ON = 'gray30'
COLOR_OFF = 'LightSteelBlue1'

def draw_arrow(i, j, drn):
    sep = UNIT // 8
    east = (sep, UNIT // 2)
    west = (UNIT - sep, UNIT // 2)
    north = (UNIT // 2, sep)
    south = (UNIT // 2, UNIT - sep)
    x, y = j * UNIT, i * UNIT
    if drn == (0, 1):
        A = (x + east[0], y + east[1])
        B = (x + west[0], y + west[1])
    elif drn ==  (-1, 0):
        A = (x + south[0], y + south[1])
        B = (x + north[0], y + north[1])
    elif drn ==  (0, -1):
        B = (x + east[0], y + east[1])
        A = (x + west[0], y + west[1])
    else:
        B = (x + south[0], y + south[1])
        A = (x + north[0], y + north[1])
    return cnv.create_line(
        A,
        B,
        width=ARROW_WIDTH,
        arrow='last',
        fill='red',
        arrowshape=(18, 30, 8))


def draw_square(i, j):
    x, y = j * UNIT, i * UNIT
    square = cnv.create_rectangle((x, y), (x + UNIT, y + UNIT),
                                  fill=COLOR_ON,
                                  outline='')
    cnv.tag_lower(square)
    return square


def draw(pos, drn, arrow):
    cnv.delete(arrow)
    (ii, jj), ndrn = bouger(pos, drn, items)
    i, j = pos
    square = items[i][j]

    if square == 0:
        square = draw_square(i, j)
        items[i][j] = square
    else:
        cnv.delete(square)
        items[i][j] = 0

    narrow = draw_arrow(ii, jj, ndrn)
    return (ii, jj), ndrn, narrow

def bouger(pos, drn, items):
    i, j = pos
    a, b = drn
    aa, bb = (b, -a) if items[i][j] == 0 else (-b, a)
    return (i + aa, j + bb), (aa, bb)

def anim():
    global pos, drn, arr, id_anim, stop
    if not stop:
        pos, drn, arr = draw(pos, drn, arr)
    id_anim = cnv.after(DELAY, anim)



root = Tk()
cnv = Canvas(root, width=WIDTH, height=HEIGHT, background=COLOR_OFF)
cnv.pack(side=LEFT)

nwidth = WIDTH // UNIT
nheight = HEIGHT // UNIT


def make_grid():
    for i in range(nwidth):
        cnv.create_line((i * UNIT, 0), (i * UNIT, HEIGHT), fill=COLOR_GRID)
    for i in range(nheight):
        cnv.create_line((0, i * UNIT), (WIDTH, i * UNIT), fill=COLOR_GRID)


def init():
    global items, pos, drn, arr, stop
    cnv.delete("all")
    cnv.focus_set()
    make_grid()

    items = [[0] * nwidth for _ in range(nheight)]
    pos = (nheight // 2, nwidth // 2)
    drn = (1, 0)
    arr = draw_arrow(pos[0], pos[1], drn)
    stop = True
    anim()


def on_off(event):
    global stop
    stop = not stop


def again(event):
    cnv.after_cancel(id_anim)
    init()


cnv.bind("<space>", on_off)
cnv.bind("<Escape>", again)


init()
root.mainloop()

• Ligne 99 : pour que le canevas puisse réagir aux appuis sur les touches il doit avoir la focus.
• Ligne 116 : quand l’application est réinitialisée, il faut supprimer l’animation précédente, cf. ligne 77.

Prolongements¶

• Placer un compteur de déplacement dans un label
• Implémenter des boutons multimedia (avant, arrière, pause, etc)
• Faire une version scrollable
• Faire un applet complet, comme sur la page espagnole de Wikipedia
• Déterminer la périodicité de la répétition, colorier le motif qui se répète
• Généraliser avec une grille hexagonale et en utilisant un motif de couleurs.
• Etendre la fourmi de Langton en des turmites (contraction de Turing et Termites).