$\newcommand{\ds}{\displaystyle}$ $\newcommand{\Frac}{\ds\frac}$ $\renewcommand{\r}{\mathbb{ R}}$ $\newcommand{\C}{\mathbb{ C}}$ $\newcommand{\n}{\mathbb{ N}}$ $\newcommand{\z}{\mathbb{ Z}}$ $\newcommand{\Q}{\mathbb{ Q}}$ $\newcommand{\N}{\mathbb{ N}}$ $\newcommand{\n}{\mathbb{ N}}$ $\newcommand{\ol}{\overline}$ $\newcommand{\abs}[1]{\left| \,{#1} \right|}$ $\newcommand{\pv}{\;;\;}$ $\newcommand{\ens}[1]{\left\{ {#1} \right\}}$ $\newcommand{\mens}[1]{\setminus\left\{ {#1} \right\}}$ $\newcommand{\Par}[1]{\left({#1}\right)}$

Les tables de Micmaths¶

Version du 17/04/2021

Objectif et prérequis de l’activité¶

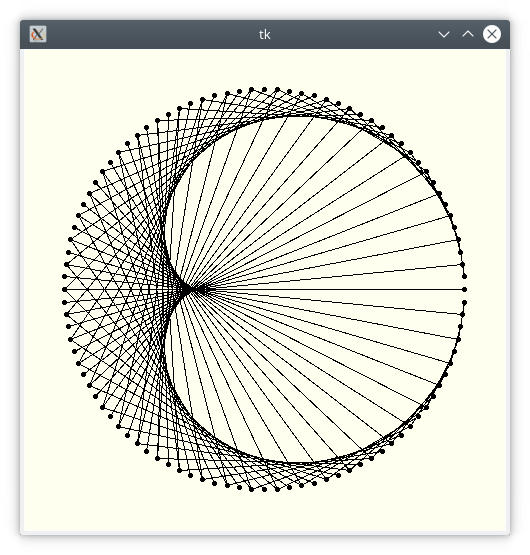
Cette activité a pour but de construire une interface graphique sous Tkinter représentant les tables de multiplication selon la vidéo Youtube de Micmaths intitulée la face cachée des tables de multiplications. Une fois l’interface réalisée, on obtiendra quelque chose comme ceci :

../../../../_images/tables_micmaths_continu.gif

Cette activité donne l’occasion de travailler différentes questions de mathématiques simples :

le « modulo », c’est-à-dire le reste de la division entière qui permet de gérer le caractère périodique
le cercle trigonométrique et les angles,
le changement de repère.

Concernant Python, il suffit d’être à l’aise avec les rudiments, cf. mon cours de découverte (lien pdf) notamment

l’opérateur modulo,
les boucles for,
les fonctions.

J’utiliserai aussi des listes en compréhension mais on pourrait s’en passer.

Concernant Tkinter, voici l’essentiel de ce qu’il faut connaître :

quelques éléments sur les fenêtres et widgets, avoir bien compris le repérage dans un canevas
savoir dessiner des segments et des cercles
savoir créer et utiliser un curseur.

Précision quant à l’origine de cette représentation des tables : Burkard Polster, dans la présentation d”une de ses vidéos, attribue la découverte de cette représentation à Simon Plouffe, cf. son article curves obtained with b to the n mod p.

Présentation des tables de Micmaths¶

D’abord, quand on parle ici de table de multiplication, il y a deux extensions par rapport aux tables de l’école primaire :

on ne se restreint pas au dix premiers multiples, par exemple, on peut considérer les 100 premiers multiples de 2, après 20, et dans la table on trouve ensuite 22, 24, 26, etc jusqu’à 200 ;
on ne se restreint pas non plus aux tables de 1 à 10, par exemple, la table de 42 existe et contient 42, 84, …, 420, …

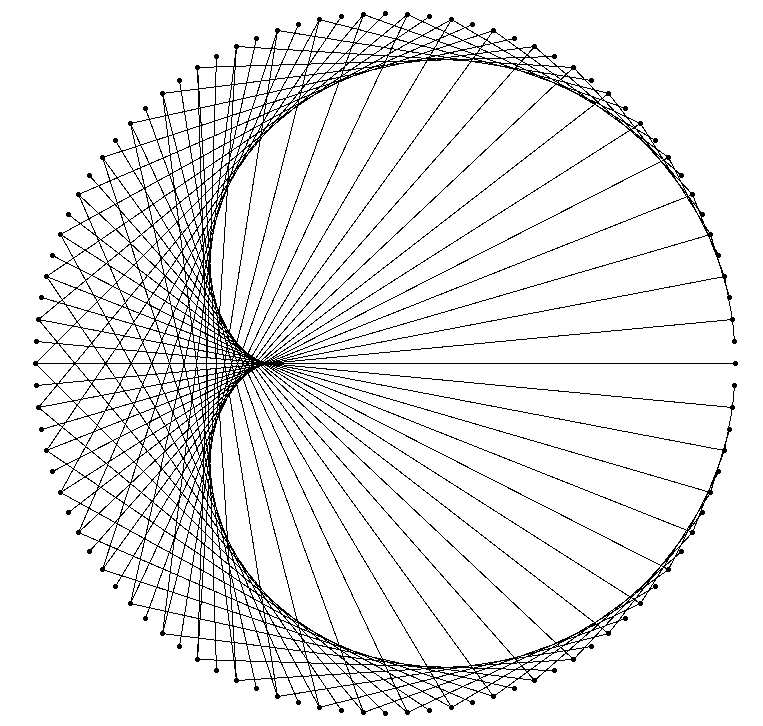
On se donne un entier $\mathtt{n}$ , ci-dessous ce sera $\mathtt{n=2}$ . Chaque ligne de la table de multiplication de $\mathtt{n}$ va être représentée par une corde sur un cercle (une corde c’est un segment qui joint deux points du cercle). Une fois la table construite, on obtiendra un motif qui peut être surprenant :

../../../../_images/table_plouffe_turtle_100.png

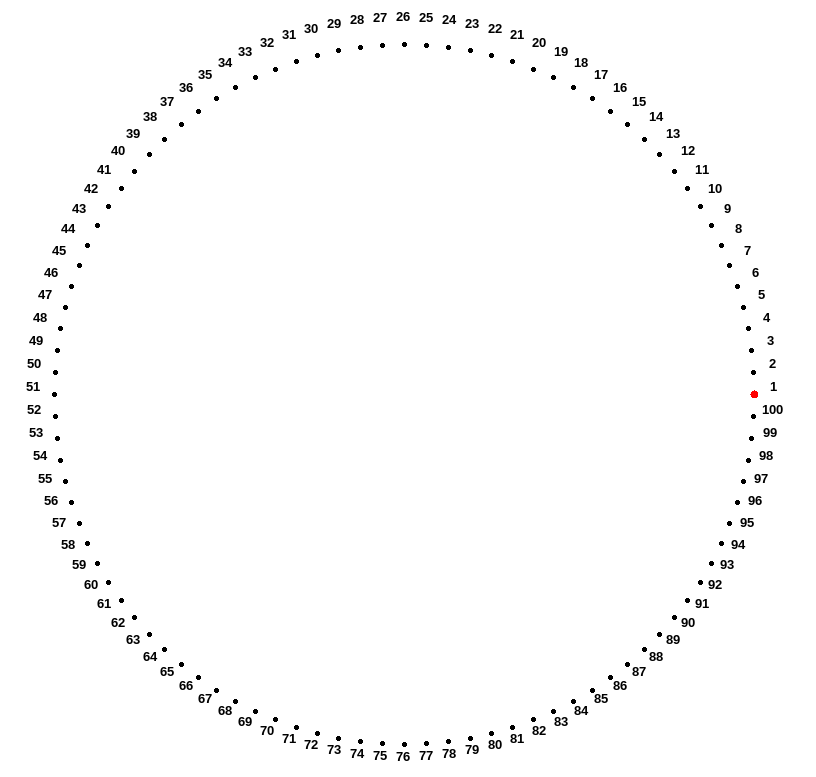
Plus précisément, on va représenter la table de multiplication de $\mathtt{n}$ à l’aide de $\mathtt{p}$ points placés sur un cercle. Pour fixer les idées, imaginons la table de $\mathtt{n=2}$ avec $\mathtt{p=100}$ points. On commence par placer $\mathtt{p}$ points régulièrement espacés sur un cercle. Le premier point placé représente l’entier 1, le 2e point représente l’entier 2 et ainsi de suite jusqu’au $\mathtt{p}$ -ème point :

../../../../_images/table_plouffe_turtle_cercle_100.png

Pour représenter des entiers plus grands que $p$ , comment fait-on ? Réponse : après avoir fait le tour, on continue à compter à partir du premier point, par exemple pour représenter $142$ , on utilise le point $42$ puisque $142=100+42$ . Plus généralement, l’entier $N$ est représenté par le reste de la division entière de $N$ par $p$ .

Maintenant, comment représente-t-on les multiplications dans la table ? Réponse : on va représenter les produits

$\mathtt{1\times n}$ , $\mathtt{2\times n}$ , …, $\mathtt{p\times n}$

par des segments. Le produit $\mathtt{k\times n}$ est représenté (cf. dessin ci-dessous) par la corde $\mathtt{AB}$ où

le point $\mathtt{A}$ représente $\mathtt{k}$ sur le cercle,
le point $\mathtt{B}$ représente sur le cercle le résultat du produit $\mathtt{k\times n}$ .

Voici un exemple, dans le cas $\mathtt{n=2}$ et $\mathtt{p=100}$ , du produit $\mathtt{k\times n}$ avec $\mathtt{k=73}$ :

../../../../_images/table_plouffe_turtle_produit.png

Comme on a $73\times 2=146$ qui est représenté par 46, on relie le point $A$ représentant $73$ et le point $B$ représentant $46$ (le résultat).

Lorsque les $\mathtt{p}$ « produits » sont dessinés, on obtient un motif, par exemple, la figure montrée plus haut correspond à $\mathtt{n=2}$ et $\mathtt{p=100}$ .

Le but est de réaliser une interface graphique comme ci-dessous :

et qui permette à l’aide de deux curseurs de faire varier la valeur $\mathtt{n}$ de la table et le nombre $\mathtt{p}$ de sommets sur le cercle.

Auparavant, on réalisera le motif sans curseur.

Par ailleurs, comme c’est fait dans la vidéo de Micmaths, on implémentera pour finir le cas de tables de multiplication non entière, par exemple la table de 4.2, ce qui permet de présenter de jolis motifs de transition entre tables entières.

Le choix du repère¶

Cette notion de changement de repère a déjà été exposée. Je la reprends toutefois pour les besoins de l’exercice.

Le repère de Tkinter n’est pas placé comme on en a l’habitude pour faire des calculs mathématiques, il oblige à mettre la tête à l’envers :

Pour faciliter notre tâche, on va faire les calculs dans un repère orienté comme on en a l’habitude et centré où on en a besoin puis on transmettra au canevas de Tkinter les points correspondants grâce à une formule de changement de repère.

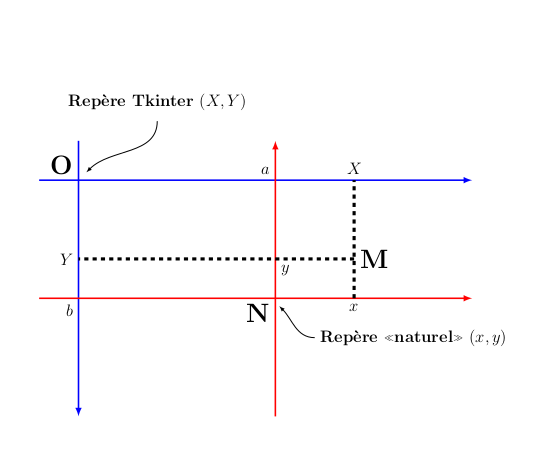
Ci-dessous, on distingue deux repères :

le repère d’origine, en bleu, celui du canevas de Tkinter, centré en $O$ en haut à gauche
un autre, en rouge, centré en $N$ (comme Nouveau) et orienté de manière traditionnelle (axe des abscisses orienté de gauche à droite, axe des ordonnées orienté de bas en haut)

Supposons que dans le repère Tkinter on ait $N=(a,b)$ . Alors si $M$ est un point quelconque du canevas tel que :

dans le repère $O$ , on ait $M=(X,Y)$ (en lettres majuscules)
dans le repère $N$ , on ait $M=(x,y)$ (en minuscule)

alors, facilement, on voit que

$\begin{cases}X=a+x\\Y=b-y\end{cases}$

d’où la fonction suivante qui va nous donner des coordonnées $(X, Y)$ dans le repère centré en $O$ d’un point de coordonnées $(x, y)$ dans le repère centré en $N$ :

def passage(x,y, a, b):
    return (a+x, b-y)

Désormais on peut faire tous les calculs dans le nouveau repère (d’origine N) et pour l’affichage des points par Tkinter, on transmettra les bonnes coordonnées en utilisant la fonction passage ci-dessus.

L’intérêt pour nous est que les calculs vont utiliser des points placés sur un cercle de centre $\mathtt{N}$ .

Simplification de la numérotation¶

Dans notre présentation des tables, les points du cercle sont numérotés à partir de 1. En fait, pour le calcul, il sera plus simple de décaler la numérotation à partir de 0. Autrement dit, les $p$ points du cercle seront indexés par

$\mathtt{0, 1, \dots, p-1}$

autrement dit dans range(p).

Il y a deux intérêts à cela. Pour le point indexé $k$

le calcul du produit de $m=k\times b$ se fera directement en prenant son reste modulo $n$ c’est-à-dire m % n ;
l’angle au centre $(OA, OM)$ vaut $k\alpha$ où $\alpha=2\pi/p$ est l’angle qui se répète $p$ fois tout autour du cercle.

Le point indexé $k$ a donc pour coordonnées $(R\times \cos (2k\pi/p), R\times \sin (2k\pi/p))$ où R est le rayon du cercle.

Tracé du cercle et de ses sommets¶

On va réaliser une table de multiplication statique, c’est-à-dire que $n$ et $p$ ne seront pas variables, ils seront donnés au départ, dans l’exemple, ce sera $\mathtt{n=2}$ et $\mathtt{p=100}$ . Du point de vue du dessin, il y aura juste un canevas, sans les curseurs.

Précisons une fois encore que tous les calculs de coordonnées se font dans le nouveau repère d’origine $\mathtt{N}$ .

Tracé des sommets sur le cercle¶

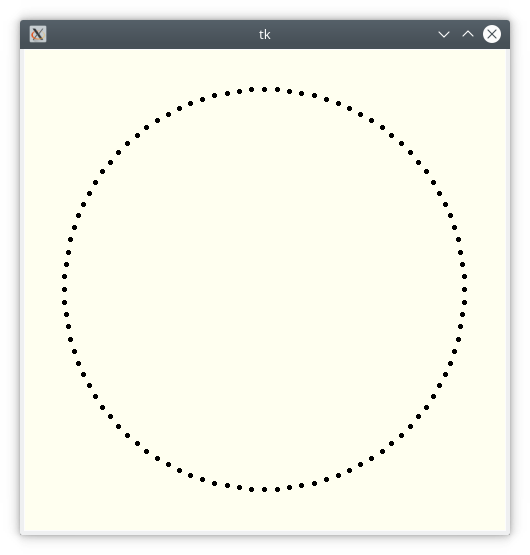
Pour l’instant, on ne s’occupe pas de la table de $n$ . On va d’abord placer nos $\mathtt{p}$ sommets sur le cercle qui sera de rayon $R$ :

On utilisera les coordonnées indiquées plus haut et on convertira plus tard dans les coordonnées du canevas avec la fonction passage.

On aura besoin d’une fonction qui place un sommet comme une petite bulle noire. On utilisera pour cela la fonction suivante :

def dot(cnv, C, R=6, color='red'):
    xC, yC=C
    return cnv.create_oval(xC-R,yC-R,xC+R, yC+R, fill=color,
    outline=color)

Le code de cette fonction est expliqué dans la documentation.

Tout le code à écrire sera placé dans des fonctions, c’est une bonne pratique et cela assure une bonne lisibilité du code.

On va créer un canevas :

master=Tk()
a=b=1.2*R
cnv=Canvas(master, width=2*a, height=2*b, bg='ivory')
cnv.pack()

Ici, master est la fenêtre principale. Les valeurs a et b sont les coordonnées du centre du cercle qui sera de rayon R. Il est écrit 1.2*R au lieu de R pour disposer d’une marge autour du cercle dans le canevas cnv. Le canevas est ensuite intégré à la fenêtre avec la méthode pack.

Ensuite

t=2*pi/p
base=[(R*cos(k*t), R*sin(k*t)) for k in range(p)]
draw_base(cnv, base, a, b)

on place dans une liste base les p petites bulles noires régulièrement espacées d’un angle $\mathtt{t=2\pi/p}$ et qui composent le cercle. Noter que les coordonnées sont calculées dans « notre » repère habituel en maths, et pas dans le repère de Tkinter. Puis on appelle une fonction draw_base qui dessine les sommets sur le canevas.

On définit maintenant la fonction draw_base :

def draw_base(cnv, base, a, b):
    p=len(base)
    for k in range(p):
        x, y=base[k]
        X, Y=passage(x, y, a, b)
        dot(cnv, (X, Y), R=2, color='black')

Elle a besoin de a et de b pour effectuer le changement de base afin que le placement puisse être fait dans le repère de Tkinter. On parcourt la liste des sommets, on convertit chaque point $\mathtt{(x, y)}$ en ses coordonnées (X, Y) dans le repère de Tkinter et on demande à Tkinter avec la fonction dot de dessiner le point $\mathtt{(X, Y)}$ .

Il ne reste plus qu’à mettre tout ce code en forme, ce qui donne :

cercle_dots.py

from tkinter import Tk, Canvas
from math import sin, cos, pi

def passage(x,y, a, b):
    return (a+x, b-y)

def dot(cnv, C, R=6, color='red'):
    xC, yC=C
    return cnv.create_oval(xC-R,yC-R,xC+R, yC+R, fill=color,
                           outline=color)

def draw_base(cnv, base, a, b):
    p=len(base)
    for k in range(p):
        x, y=base[k]
        X, Y=passage(x, y, a, b)
        dot(cnv, (X, Y), R=2, color='black')

def draw(n, p, R):
    master=Tk()
    a=b=1.2*R
    cnv=Canvas(master, width=2*a, height=2*b, bg='ivory')
    cnv.pack()
    t=2*pi/p
    base=[(R*cos(k*t), R*sin(k*t)) for k in range(p)]
    draw_base(cnv, base, a, b)
    master.mainloop()

p=100
R=200
n=2
draw(n, p, R)

et qui affiche :

Tracé du motif¶

Il ne reste plus qu’à tracer les segments (les cordes du cercle). On va construire la table de n, dans l’exemple n=2. On choisira p=100 points sur le cercle.

On peut écrire une fonction qui calcule le produit $\mathtt{k\times n}$ dans la table de n :

produit.py

def produit(k, n, p):
    return k*n % p

k=73
n=2
p=100
print("%s x %s = %s" %(k, n, produit(k, n, p)))

8	73 x 2 = 46

On a juste appliqué la règle qui définit notre table de multiplication.

On définit maintenant une fonction segment qui trace le segment correspondant au produit dans la table de l’élément d’indice k :

def passage(x,y, a, b):
    return (a+x, b-y)

def produit(k, n, p):
    return k*n % p

def segment(cnv, k, n, p, base, a, b):
    prod=produit(k, n, p)
    xS, yS=base[k]
    xT, yT=base[prod]
    S=passage(xS, yS, a, b)
    T=passage(xT, yT, a, b)
    cnv.create_line(S, T)

Le centre du cercle a pour coordonnées (a, b) dans le repère de Tkinter et base est la liste des coordonnées des p sommets sur le cercle. La fonction segment crée le segment entre le point S du cercle d’indice k et le point T du cercle représentant le produit $\mathtt{k\times n}$ . Donc, on calcule d’abord le produit (ligne 8), on récupère le point $\mathtt{S}$ par ses coordonnées dans le repère centré au milieu du canevas (ligne 9), on récupère de même le point $\mathtt{T}$ correspondant au produit $\mathtt{k\times n}$ (ligne 10). On calcule les coordonnées de ces points dans le repère de Tkinter (lignes 11-12) et on trace le segment sur le canevas (ligne 13).

Il ne reste plus qu’à compléter le code de cercle_dots.py :

tables_statiques.py

from tkinter import Tk, Canvas
from math import sin, cos, pi

def passage(x,y, a, b):
    return (a+x, b-y)

def produit(k, n, p):
    return k*n % p

def segment(cnv, k, n, p, base, a, b):
    prod=produit(k, n, p)
    xA, yA=base[k]
    xB, yB=base[prod]
    A=passage(xA, yA, a, b)
    B=passage(xB, yB, a, b)
    cnv.create_line(A, B)

def dot(cnv, C, R=6, color='red'):
    xC, yC=C
    return cnv.create_oval(xC-R,yC-R,xC+R, yC+R, fill=color, outline=color)

def draw_base(cnv, base, a, b):
    p=len(base)
    for k in range(p):
        x, y=base[k]
        X, Y=passage(x, y, a, b)
        dot(cnv, (X, Y), R=2, color='black')

def draw(n, p, R):
    master=Tk()
    a=b=1.2*R
    cnv=Canvas(master, width=2*a, height=2*b, bg='ivory')
    cnv.pack()

    t=2*pi/p
    base=[(R*cos(k*t), R*sin(k*t)) for k in range(p)]
    draw_base(cnv, base, a, b)

    for k in range(p):
        segment(cnv, k, n, p, base, a, b)
    master.mainloop()

n=2
p=100
R=200
draw(n, p, R)

Le code a été complété essentiellement aux lignes 39-40 (la boucle de parcours pour tracer les segments). On obtient cette fenêtre :

Pour obtenir des motifs différents, il suffit de changer les valeurs de n et p (a priori, dans le code, lignes 43-44).

Générer le motif avec deux curseurs¶

Pour finir, il ne reste plus qu’à se donner la possibilité de visualiser les motifs sans quitter l’interface graphique. Une bonne solution pour cela est d’utiliser deux curseurs, l’un jouant sur la valeur n de la table et l’autre sur le nombre de points :

../../../../_images/tables_micmaths_discret.gif

Il s’agit de reprendre l’essentiel du code de tables_statiques.py sauf que n et p doivent être capturés par les curseurs. Codons les curseurs :

# Position de départ
p=100 # nombre de points sur le cercle
R=200
n=5 # Table de n

N=P=2

master=Tk()
a=b=1.2*R
cnv=Canvas(master, width=2*a, height=2*b, bg='ivory')
cnv.pack(side="left")

table_slider = Scale(master, label="Table de ...",
                     font="Arial 15 bold",
                     orient = "horizontal", command=table,
                     from_=2, to=50, length=250)
table_slider.pack(pady=15)

vertex_slider = Scale(master, label="Nombre de sommets",
                      font="Arial 15 bold",
                      orient = "horizontal", command=vertex,
                      from_=2, to=200, length=250)
vertex_slider.pack(pady=5)

master.mainloop()

On définit chaque curseur aux lignes 13 et 19, et on les place avec la méthode pack (lignes 17 et 23).

Fixons notre attention sur le curseur des tables, le principe étant le même pour l’autre curseur. Le curseur des tables capture toutes les tables de 2 à 50 (ligne 16). Le curseur est placé horizontalement (ligne 15) et est de longueur 250 pixels. Chaque fois que l’utilisateur bouge le curseur, la fonction table vers laquelle l’option command pointe est appelée (ligne 15). Cette fonction est appelée sous la forme table(n) où n est la valeur lue par le curseur (entre 2 et 50). L’argument n est passé sous forme de chaîne de caractères représentant le nombre en base 10. Par exemple, si le curseur est bougé bascule à la position 42, on a un appel table("42").

Les variables N et P sont des variables globales destinées à mémoriser l’état actuel des valeurs de n et p et utilisées par les fonctions de rappel table et vertex (ligne 21).

Examinons maintenant la fonction table :

def table(value):
    global N
    N=int(value)
    show(N, P)

def show(n,p):
    cnv.delete("all")
    t=2*pi/p
    base=[(R*cos(k*t), R*sin(k*t)) for k in range(p)]
    draw_base(cnv, base, a, b)

    for k in range(p):
        segment(cnv, k, n, p, base, a, b)

Lorsque par exemple table("42") est appelé, le code lignes 1-4 est appelé. La valeur lue (ici 42) est mise-à-jour dans la variable globale N (après conversion en un entier puisque la valeur est la chaîne "42") ; la fonction show qui redessine le canevas est appelée pour dessiner le plateau. La fonction show est basée sur la fonction draw du code tables_statiques.py. La seule différence est que tout le canevas est effacé (ligne 7) avant d’être redessiné avec les nouvelles valeurs.

Voici le code complet :

tables_curseurs.py

from tkinter import Tk, Canvas, Scale
from math import sin, cos, pi

def passage(x,y, a, b):
    return (a+x, b-y)

def produit(k, n, p):
    return k*n % p

def segment(cnv, k, n, p, base, a, b):
    prod=produit(k, n, p)
    xA, yA=base[k]
    xB, yB=base[prod]
    A=passage(xA, yA, a, b)
    B=passage(xB, yB, a, b)
    cnv.create_line(A, B)

def dot(cnv, C, R=6, color='red'):
    xC, yC=C
    return cnv.create_oval(xC-R,yC-R,xC+R, yC+R, fill=color,
                           outline=color)

def draw_base(cnv, base, a, b):
    p=len(base)
    for k in range(p):
        x, y=base[k]
        X, Y=passage(x, y, a, b)
        dot(cnv, (X, Y), R=2, color='black')

def table(value):
    global N
    N=int(value)
    show(N, P)

def vertex(value):
    global P
    P=int(value)
    show(N, P)

def show(n,p):
    cnv.delete("all")
    t=2*pi/p
    base=[(R*cos(k*t), R*sin(k*t)) for k in range(p)]
    draw_base(cnv, base, a, b)

    for k in range(p):
        segment(cnv, k, n, p, base, a, b)

# Position de départ
p=100 # nombre de points sur le cercle
R=200
n=5 # Table de n

N=P=2

master=Tk()
a=b=1.2*R
cnv=Canvas(master, width=2*a, height=2*b, bg='ivory')
cnv.pack(side="left")

table_slider = Scale(master, label="Table de ...",
                     font="Arial 15 bold",
                     orient = "horizontal", command=table,
                     from_=2, to=50, length=250)
table_slider.pack(pady=15)

vertex_slider = Scale(master, label="Nombre de sommets",
                      font="Arial 15 bold",
                      orient = "horizontal", command=vertex,
                      from_=2, to=200, length=250)
vertex_slider.pack(pady=5)

master.mainloop()

Nettoyage de code¶

La fin du code n’est pas écrite dans une fonction, ce qui est peu lisible. On peut y remédier au prix de la déclaration en global de certaines variables :

tables_curseurs_fonction.py

from tkinter import Tk, Canvas, Scale
from math import sin, cos, pi

def passage(x,y, a, b):
    return (a+x, b-y)

def produit(k, n, p):
    return k*n % p

def segment(cnv, k, n, p, base, a, b):
    prod=produit(k, n, p)
    xA, yA=base[k]
    xB, yB=base[prod]
    A=passage(xA, yA, a, b)
    B=passage(xB, yB, a, b)
    cnv.create_line(A, B)

def dot(cnv, C, R=6, color='red'):
    xC, yC=C
    return cnv.create_oval(xC-R,yC-R,xC+R, yC+R, fill=color,
                           outline=color)

def draw_base(cnv, base, a, b):
    p=len(base)
    for k in range(p):
        x, y=base[k]
        X, Y=passage(x, y, a, b)
        dot(cnv, (X, Y), R=2, color='black')

def table(value):
    global N
    N=int(value)
    show(cnv, N, P)

def vertex(value):
    global P
    P=int(value)
    show(cnv, N, P)

def show(cnv, n, p):
    cnv.delete("all")
    t=2*pi/p
    base=[(R*cos(k*t), R*sin(k*t)) for k in range(p)]
    draw_base(cnv, base, a, b)

    for k in range(p):
        segment(cnv, k, n, p, base, a, b)

def demo():
    global N, P, cnv, R, a, b
    # Position de départ
    p=100 # nombre de points sur le cercle
    R=200
    n=2 # Table de n

    N=P=2

    master=Tk()
    a=b=1.2*R
    cnv=Canvas(master, width=2*a, height=2*b, bg='ivory')
    cnv.pack(side="left")

    table_slider = Scale(master, label="Table de ...",
                        font="Arial 15 bold",
                        orient = "horizontal", command=table,
                        from_=2, to=50, length=250)
    table_slider.pack(pady=15)

    vertex_slider = Scale(master, label="Nombre de sommets",
                        font="Arial 15 bold",
                        orient = "horizontal", command=vertex,
                        from_=2, to=200, length=250)
    vertex_slider.pack(pady=5)

    master.mainloop()

demo()

Expliquons les déclarations global aux lignes 50, 31 et 36 :

pour les variables cnv, a, b et R, c’est uniquement un problème de lecture de ces variables qui sont masquées par la fonction demo. Par exemple, sans déclaration global, la fonction show ne peut accéder à R qu’elle utilise ligne 43 (ou alors, il faudrait redéfinir show et placer R en paramètre) ;
pour N et P, c’est un problème d”écriture car ces variables doivent être modifiées tout du long du programme, plus précisément, par les fonction table et vertex (lignes 32 et 37).

Utiliser une classe¶

On peut encore améliorer la lisibilité du code en écrivant une classe :

tables_curseurs_classe.py

from tkinter import Tk, Canvas, Scale
from math import sin, cos, pi

def passage(x,y, a, b):
    return (a+x, b-y)

def produit(k, n, p):
    return k*n % p

def dot(cnv, C, R=6, color='red'):
    xC, yC=C
    return cnv.create_oval(xC-R,yC-R,xC+R, yC+R, fill=color,
                           outline=color)
class TablesMult:

    def __init__(self, R=200):
        self.R=R
        self.a=self.b=R*1.2
        self.n=self.p=2

    def segment(self, k, base, n, p):
        prod=produit(k, n, p)
        xA, yA=base[k]
        xB, yB=base[prod]
        A=passage(xA, yA, self.a, self.b)
        B=passage(xB, yB, self.a, self.b)
        self.cnv.create_line(A, B)

    def draw_base(self, base):
        p=len(base)
        for k in range(p):
            x, y=base[k]
            X, Y=passage(x, y, self.a, self.b)
            dot(self.cnv, (X, Y), R=2, color='black')

    def table(self, value):
        self.n=int(value)
        self.show()

    def vertex(self, value):
        self.p=int(value)
        self.show()

    def show(self):
        self.cnv.delete("all")
        t=2*pi/self.p
        base=[(self.R*cos(k*t), self.R*sin(k*t))
              for k in range(self.p)]
        self.draw_base(base)

        for k in range(self.p):
            self.segment(k, base, self.n, self.p)

    def demo(self):
        # Position de départ
        master=Tk()
        self.cnv=Canvas(master, width=2*self.a, height=2*self.b,
                        bg='ivory')
        self.cnv.pack(side="left")

        table_slider = Scale(master, label="Table de ...",
                            font="Arial 15 bold",
                            orient = "horizontal",
                            command=self.table,
                            from_=2, to=50, length=250)
        table_slider.pack(pady=15)

        vertex_slider = Scale(master, label="Nombre de sommets",
                            font="Arial 15 bold",
                            orient = "horizontal",
                            command=self.vertex,
                            from_=2, to=200, length=250)
        vertex_slider.pack(pady=5)

        master.mainloop()

table=TablesMult()
table.demo()

Tables à valeurs flottantes¶

Dans sa vidéo, Micmaths a la très bonne idée de passer continuement de la table de n à la table de n+1. Autrement dit, on va aussi représenter par exemple la table de 2,62. L’intérêt est qu’on voit se déformer par exemple la table de 2 en la table de 3.

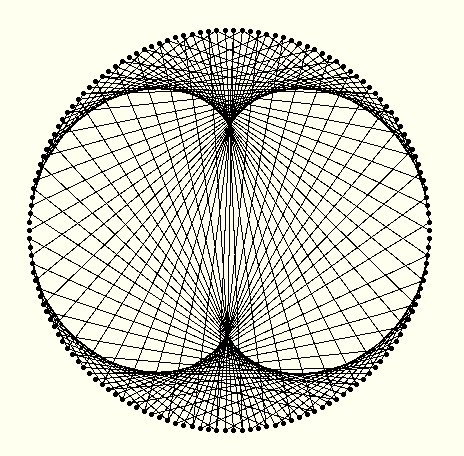
Ainsi, avec 150 sommets, la table de 2 à la forme suivante :

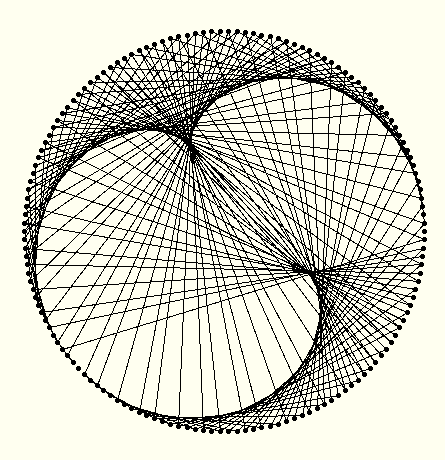
Elle contient un seul point singulier. La table de 3 a la forme suivante

et elle contient deux points singuliers.

Et voici la table de 2,62 :

on voit bien le 2e point singulier en formation.

Que faut-il changer dans le code des tables entières ?

Pour le calcul des valeurs de la table de n, par exemple de $\mathtt{k\times n}$ , on effectue à nouveau le produit, ce qui donne un flottant (puisque n est flottant cette fois) qu’on va appeler u. Prendre le reste d’un flottant par un entier a un sens, par exemple, le reste de 42,75 par 10 est le flottant 2,75 et se calcule par 42.75 % 10. Donc, on peut prendre le reste r de u modulo $\mathtt{p}$ , ce qui donne un flottant. Pour pouvoir placer le point correspondant sur le cercle, on prendra tout simplement la partie entière int(r) de ce reste.
Pour la partie graphique, il suffit de pouvoir progresser avec un curseur par pas plus petit qu’une unité, par exemple, par pas de 1/100. Il suffit d’utiliser pour cela l’option resolution du widget Scale, par exemple

table_slider = Scale(master, from_=2, to=6, resolution=0.01)

Cela signifie qu’on pourra progresser avec le curseur suivant les valeurs :

2.00 2.01 2.02 ...5.98 5.99 6.00

D’où le code final suivant :

tables_curseurs_continu.py

from tkinter import Tk, Canvas, Scale
from math import sin, cos, pi

def passage(x,y, a, b):
    return (a+x, b-y)

def produit(k, n, p):
    return int(k*n % p)

def segment(cnv, k, n, p, base, a, b):
    prod=produit(k, n, p)
    xA, yA=base[k]
    xB, yB=base[prod]
    A=passage(xA, yA, a, b)
    B=passage(xB, yB, a, b)
    cnv.create_line(A, B)

def dot(cnv, C, R=6, color='red'):
    xC, yC=C
    return cnv.create_oval(xC-R,yC-R,xC+R, yC+R, fill=color,
                           outline=color)

def draw_base(cnv, base, a, b):
    p=len(base)
    for k in range(p):
        x, y=base[k]
        X, Y=passage(x, y, a, b)
        dot(cnv, (X, Y), R=2, color='black')

def table(value):
    global N
    N=float(value)
    show(cnv, N, P)

def vertex(value):
    global P
    P=int(value)
    show(cnv, N, P)

def show(cnv, n, p):
    cnv.delete("all")
    t=2*pi/p
    base=[(R*cos(k*t), R*sin(k*t)) for k in range(p)]
    draw_base(cnv, base, a, b)

    for k in range(p):
        segment(cnv, k, n, p, base, a, b)

def demo():
    global N, P, cnv, R, a, b
    # Position de départ
    p=100 # nombre de points sur le cercle
    R=200
    n=2 # Table de n

    N=P=2

    master=Tk()
    a=b=1.2*R
    cnv=Canvas(master, width=2*a, height=2*b, bg='ivory')
    cnv.pack(side="left")

    table_slider = Scale(master, label="Table de ...",
                        font="Arial 15 bold",
                        orient = "horizontal", command=table,
                        from_=2, to=6, resolution=0.01,
                        length=350)
    table_slider.pack(pady=15)

    vertex_slider = Scale(master, label="Nombre de sommets",
                        font="Arial 15 bold",
                        orient = "horizontal", command=vertex,
                        from_=2, to=200, length=350)
    vertex_slider.pack(pady=5)

    master.mainloop()

demo()

La fonction produit a été modifiée (ligne 8). La résolution du curseur de tables a été ajoutée (ligne 66). La variable globale N modifiée par la fonction de rappel table est devenue une variable flottante (cf. ligne 32).

La cardioïde de la table de 2¶

Cette section nécessite quelques connaissances de mathématiques post-bac (équations paramétriques d’une courbe, enveloppe d’une famile de droites) et utilisera le module de calcul formel Sympy. Les codes Python sont accessibles en ligne sur Google Colab.

Montrons que la courbe définie par la table de 2 est une vraie cardioïde :

Comme son nom l’indique, une cardioïde est une courbe en forme de cœur et elle est susceptible d’être définie de multiples façons dont son équation polaire (qu’on utilisera).

Ainsi qu’on le voit, la figure qui apparaît n’est autre que l’enveloppe des cordes du cercle, c’est-à-dire que les droites sont justement tangentes à la courbe qui naturellement apparaît. Or, si on connaît l’équation cartésienne de chaque droite, la théorie des enveloppes permet de déterminer une équation paramétrique de la courbe.

Entrons dans le détail. Les droites de la table de deux passent par les points

$A=(\cos(2k\pi/p), \sin(2k\pi/p))$ et $B=(\cos(4k\pi/p), \sin(4k\pi/p))$ .

On est donc amené à examiner la famille de droites $(D_t)$ paramétrées par $t\in[0, 2\pi]$ et passant par les deux points $A(t)=(\cos(t), \sin(t))$ et $B(t)=A(2t)$ . Le vecteur $B(t)-A(t)$ est un vecteur directeur de la droite. On sait que, d’une manière générale, la droite d’équation cartésienne $ux+vy+w=0$ admet pour vecteur directeur le vecteur $(-v, u)$ . Donc on pose ici $(-v, u)=B(t)-A(t)$ (en sorte que $u$ et $v$ sont des fonctions de $t$ ) et on écrit l’équation cartésienne de la droite $(D_t)$ , à savoir $d(t)=0$ où $d(t)=u\times(x-\cos(t))+v\times(y-\sin(t))$ . Ensuite, conformément à la « théorie » référencée ci-dessus, on résout le système d’inconnue (x, y) défini par

$\begin{cases}d(t)=0\\d'(t)=0\end{cases}$

où $d'(t)$ est la dérivée de $d(t)$ par rapport à $t$ , étant entendu que $x$ et $y$ sont vus comme des constantes dans $d(t)$ . Une fois ce système résolu, on obtient $x$ et $y$ comme des fonctions de $t$ et la courbe paramétrée $(x, y)=(x(t), y(t))$ est l’enveloppe recherchée.

Plutôt que de faire la résolution à la main, ce qui semble assez rébarbatif, on va s’aider du module Sympy qui permet de faire du calcul formel en Python. Pour installer Sympy (sous Linux, sans doute aussi sous d’autres systèmes), il suffit de taper dans un terminal système la commande

pip3 install sympy

Voici le code qui définit et résout le système :

from sympy import *

x, y, t=symbols("x y t")

A = Matrix([cos(t), sin(t)])
B= A.subs(t, 2*t)
V= B-A

v=-V[0]
u=V[1]

D=u*(x-A[0])+v*(y-A[1])
DD=diff(D, t)

sols=linsolve([D, DD], (x, y))

L=list(sols)
print(L)

[((-3*cos(t) + cos(3*t) + 2)/(6*(cos(t) - 1)),
 2*sin(t)**3/(-3*cos(t) + 3))]

Lignes 5-6 : on définit $A$ et $B$ comme expliqué précédemment
Ligne 7 : on calcule le vecteur directeur $V$ .
Lignes 12-13 : on en déduit l’équation de la droite et on la dérive par rapport à $t$ (ligne 13).
Ligne 15 : on demande ensuite à Sympy de résoudre le système linéaire dont la solution est renvoyée sous forme d’ensemble.
Ligne 17 : on transforme l’ensemble en liste
Ligne 19 : on observe que Sympy a trouvé une seule solution, d’allures relativement simples.

Il ne reste plus qu’à demander à Matplotlib de nous dessiner la courbe. Le code qui suit a été écrit dans une feuille jupyter Notebook et reprend le code précédent :

import numpy as np
import matplotlib.pyplot as plt

sol=L[0]

x=sol[0]
y=sol[1]

T= np.arange(0,2.01*np.pi, 0.01)
X =[x.subs(t,v) for v in T]
Y =[y.subs(t,v) for v in T]

fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(1, 1, 1)

ax.axes.set_aspect('equal')
ax.spines['left'].set_position(("data", 0.0))
ax.spines['bottom'].set_position(("data", 0.0))
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.tick_params(labelleft=False, left=False)

plt.plot(X,Y, linewidth=4.0)
plt.show()

Lignes 6-7 : x et y sont des expressions formelles de Sympy. On fait varier $\mathtt{t}$ entre 0 et $\mathtt{2\pi}$ (un petit plus en fait, sinon, la courbe a un petit vide à cet endroit).
Ligne 9 : ici, le module Numpy ne sert qu’à disposer de $\mathtt{\pi}$ et à générer une subdivision régulière du segment $\mathtt{[0, 2\pi]}$ de pas 0.01 mais on pourrait s’en passer.
Lignes 10-11 : on génère ensuite les abscisses et les ordonnées des points correspondant à chacun des paramètres $\mathtt{t}$ dans la subdivision T.
Ligne 13 : on définit une figure Matplotlib, on ajuste sa taille par une option.
Ligne 14 : on définit ensuite une zone de dessin, appelé curieusement axes sous Matplotlib et qui n’a que très peu à voir avec des axes (de coordonnées).
Lignes 16-21 : tout ce qui suit sert à customiser le dessin pour placer les axes de coordonnées comme on en a l’habitude en math.
Ligne 23-24 : on génère le dessin (en ajustant l’épaisseur de la courbe) et on affiche la sortie.

On obtient :

Reste à montrer que cette courbe est une cardioïde (c’est vrai qu’elle y ressemble mais on ne sait jamais !). Pour cela, on cherche son équation polaire, le pôle étant le point de rebroussement visible. Ce point de rebroussement $\mathtt{A}$ est de coordonnées $\mathtt{(x, 0)}$ avec donc $\mathtt{y(t)=0}$ et donc $\mathtt{2\sin^3(t)=0}$ et donc $\mathtt{t=0}$ ou $\mathtt{t=\pi}$ . La valeur $\mathtt{t=0}$ correspond au point $\mathtt{(1, 0)}$ et donc la solution est $\mathtt{t=\pi}$ ce qui donne $\mathtt{A=(-1/3, 0)}$ . Dans le repère centré en $\mathtt{A}$ , l’équation de la courbe devient $\mathtt{X=x+1/3}$ et $\mathtt{Y=y}$ . On demande alors à Sympy de simplifier $\mathtt{X^2+Y^2}$ (ligne 22 ci-dessous):

from sympy import *

x, y, t=symbols("x y t")

A = Matrix([cos(t), sin(t)])
B=A.subs(t, 2*t)
V=B-A

v=-V[0]
u=V[1]

D=u*(x-A[0])+v*(y-A[1])
DD=diff(D, t)

sols=linsolve([D, DD], (x, y))

L=list(sols)
sol=L[0]

x=sol[0]
y=sol[1]
expr=simplify(expand_trig((x-x.subs(t,pi))**2+y**2))
print(expr)

24	4sin(t)4/(9(cos(t) - 1)**2)

C’est encore assez facilement simplifiable mais Sympy ne le voit pas. En l’aidant, ça va mieux :

expr=simplify(expand_trig((x-x.subs(t,pi))**2+y**2))
print(expr)

simplify(expr.subs(sin(t)**2, 1-cos(t)**2))

ce qui affiche :

4*(cos(t) + 1)**2/9

Donc, l’équation polaire de la courbe est

$\mathtt{\varrho=\sqrt{X^2+Y^2}=2/3(1+\cos(t))}$

et on reconnaît l”équation polaire d’une cardioïde.

Le cours de prépa de Mickael Prost (pdf web-archivé) explique très clairement la théorie des enveloppes (page 20) et traite exactement cette courbe (page 21). Ce qu’il obtient montre que le point caractéristique de la famille est au tiers de la corde, ce qui permettrait facilement de générer une petite animation de génération point par point de la courbe.