La récursivité

 Version du 06/12/2021, 98 exercices
Version du 06/12/2021, 98 exercices
Introduction et prérequis¶
La récursivité est une notion fondamentale en informatique théorique et en programmation et qui a la réputation d’être difficile, déroutante et mystérieuse voire divine.
Ce document illustre la notion de récursivité à travers des exemples progressifs, nombreux, variés et expliqués en détail. Il montre aussi les principales difficultés que l’on peut rencontrer quand on pratique la récursivité.
Pour aborder ce tutoriel, il faut connaître des éléments de Python comme dans mon cours d’introduction et l’avoir pratiqué plusieurs semaines. Il est important d’être à l’aise avec
- la notion de fonction
- le principe du passage des arguments
- le rôle de
return, - les booléens
- les instructions conditionnelles.
Plusieurs exemples utilisent des slices ce qui permet, dans certaines situations, d’alléger largement le code (au prix de copies). Si vous ne connaissez pas cette notion, vous pouvez consulter mon tutoriel sur les slices en Python.
Occasionnellement, il pourra être utilisé des listes en compréhension. J’utiliserai aussi, mais marginalement, des notions non forcément présentes dans des cours d’introduction comme des dictionnaires, l’instruction break, des docstrings, le module sys, des notions sur les chaînes de caractères, la concaténation de listes, etc.
Le cours contient plusieurs dizaines d’exercices et il est capital, pour assimiler la récursivité, de se confronter à de nombreuses situations et ainsi, acquérir une vision récursive.
Un grand merci à Diégo pour le lumineux logo de présentation de ce cours !
La récursivité, c’est juste ça ?¶
Une fonction f est dite « récursive » si la fonction f, lors de son exécution, fait un appel à … elle-même. Oui, c’est un peu curieux, comme si les pompiers appelaient les pompiers ! Ce genre de situation se rencontre parfois assez naturellement.
Ainsi, imaginons une fonction trier(a, b, c) qui renvoie la liste des trois entiers a, b et c triés dans l’ordre croissant. Par exemple,
print(trier(42, 31, 81))
devra afficher
[31, 42, 81]
L’algorithme de tri est ici très simple :
- si \(\mathtt{a\leq b}\) alors il y a trois possibilités pour
c: soit à gauche dea, soit entreaetb, soit à droite deb; - sinon, c’est pareil, il y a encore trois possibilités, mais les rôles de
aetbsont juste inversés.
D’où le code suivant :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | def trier(a, b, c):
# cas où a <= b
if a <= b <= c:
return [a,b,c]
if a <= c <= b:
return [a,c,b]
if c <= a <= b:
return [c,a,b]
# L'autre cas
if b <= a <= c:
return [b,a,c]
if b <= c <= a:
return [b,c,a]
if c <= b <= a:
return [c,b,a]
print(trier(42, 31, 81))
|
20 | [31, 42, 81]
|
Mais, les lignes 12-17 refont exactement ce que font les lignes 4-9 sauf que a et b sont échangées. Donc les lignes 12-17 sont équivalentes à un appel trier(b, a, c) de trier entre les lignes 4 et 9. D’où le code suivant :
1 2 3 4 5 6 7 8 9 10 | def trier(a, b, c):
if a <= b <= c:
return [a,b,c]
if a <= c <= b:
return [a,c,b]
if c <= a <= b:
return [c,a,b]
return trier (b,a,c)
print(trier(42, 31, 81))
|
11 | [31, 42, 81]
|
- Si \(\mathtt{a \leq b}\) alors l’appel
trier(a, b, c)exécute une des instructions lignes 2, 4 ou 6 ce qui renvoie la liste ordonnée. - Sinon, le code passe à la ligne 8 et la fonction
trierest appelée en échangeant les argumentsaetben sorte qu’à l’appel suivant, une des lignes 2, 4 ou 6 est exécutée et on obtient bien la liste triée.
La fonction trier est une fonction qui s’appelle elle-même (à la ligne 8) : c’est une fonction récursive, ce n’est pas plus compliqué que ça.
Une fonction récursive typique¶
L’exemple précédent n’est pas typique d’une fonction récursive car lorsque la fonction s’exécute, il y a tout au plus un appel récursif. Voici un exemple plus représentatif.
On va écrire une fonction récursive afficherAnnees(debut, fin) qui affiche, une par une, toutes les années depuis l’année debut jusqu’à l’année fin. Par exemple, l’appel afficherAnnees(2020, 2024) affichera :
2020
2021
2022
2023
2024
Si \(\mathtt{debut \leq fin}\), l’appel afficherAnnees(debut, fin) est équivalent aux deux actions suivantes
- afficher l’année
debut - afficher toutes les années de l’année \(\mathtt{debut+1}\) à l’année \(\mathtt{fin}\).
Or, la 2e action, par définition de la fonction afficherAnnees, peut être accomplie par un appel afficherAnnees(debut + 1, fin). On a donc le code pour une fonction récursive :
1 2 3 4 5 6 | def afficherAnnees(debut, fin):
if debut <= fin:
print(debut)
afficherAnnees(debut+1, fin)
afficherAnnees(2020, 2024)
|
La fonction afficherAnnees s’appelle elle-même ligne 4. La fonction affiche :
2020
2021
2022
2023
2024
Noter que lorsque la condition \(\mathtt{debut \leq fin}\) devient fausse, la fonction n’affiche rien et l’appel est terminé.
Pile des appels¶
Enrichissons légèrement le code de la fonction afficherAnnees :
1 2 3 4 5 6 7 8 | def afficherAnnees(debut, fin):
if debut <= fin:
print(debut)
afficherAnnees(debut+1, fin)
print("Bye bye", debut)
afficherAnnees(2020,2022)
print("FIN")
|
J’ai rajouté un affichage après l’affichage (ligne 5) pour dire « Bye Bye » à l’année qu’on vient de quitter. Il est intéressant d’observer l’affichage produit :
1 2 3 4 5 6 7 | 2020
2021
2022
Bye bye 2022
Bye bye 2021
Bye bye 2020
FIN
|
Python tutor¶
Pour bien comprendre le flux d’exécution de ce code, vous pouvez vous rendre sur le site Pythontutor. Il propose un outil en ligne permettant de visualiser l’exécution de votre code et l’état de la mémoire pendant l’exécution, en particulier de conteneurs (listes, chaînes, etc). Cet outil est en particulier très pratique pour pouvoir observer la pile des appels d’une fonction récursive.
Pour utiliser l’outil :
- se rendre sur cette page
- coller votre code dans la zone de texte
- cliquer sur le bouton Visualize Execution.
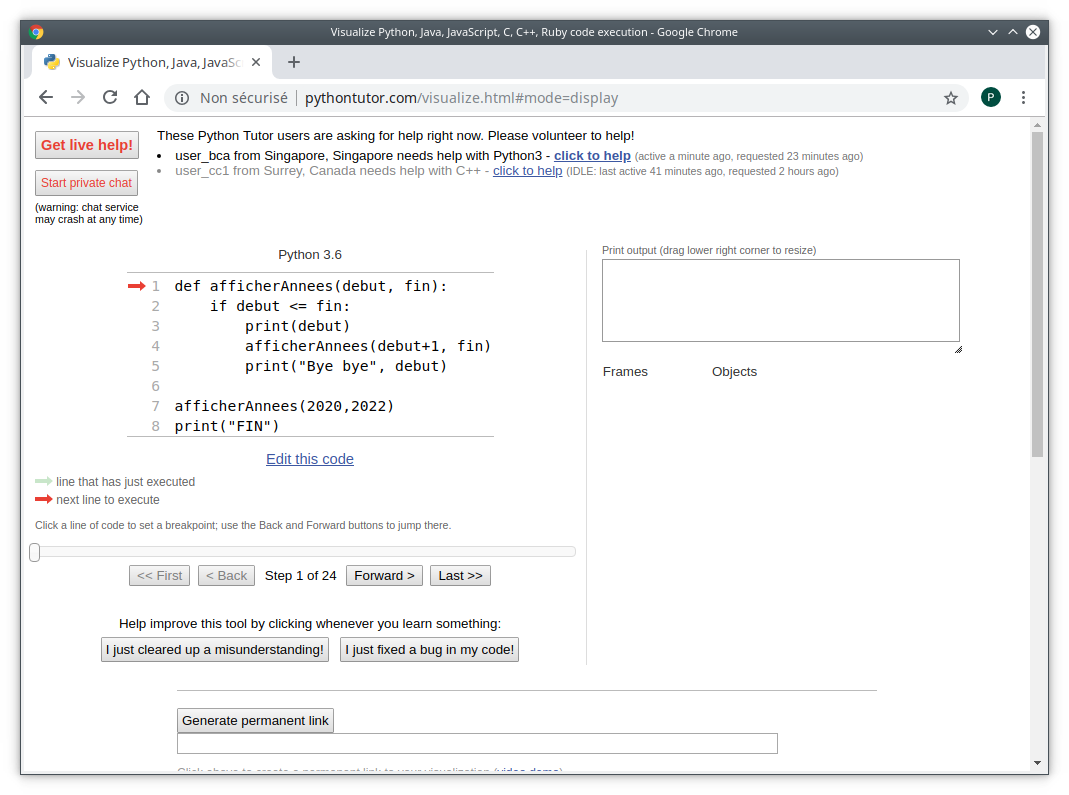
Apparaît alors une interface :
qui permet de progresser ligne à ligne (cf. la flèche rouge) dans l’exécution du code en appuyant sur le bouton Forward. Au fur et à mesure que la récursion se déroule, la pile des appels augmente ou diminue. On peut accéder au code que j’utilise ci-dessus dans Python tutor en cliquant ICI.
Faisons une description du code ci-dessus mais le mieux est d’utiliser l’outil en ligne (cf. copie d’écran ci-après). Pour une meilleure lisibilité, je reproduis le code :
1 2 3 4 5 6 7 8 | def afficherAnnees(debut, fin):
if debut <= fin:
print(debut)
afficherAnnees(debut+1, fin)
print("Bye bye", debut)
afficherAnnees(2020,2022)
print("FIN")
|
9 10 11 12 13 14 | 2020
2021
2022
Bye bye 2022
Bye bye 2021
Bye bye 20
|
- Le premier appel
afficherAnnees(2020, 2022)à la ligne 7 va provoquer l’affichage de 2020 (lignes 3 et 9 ci-dessus) et provoquer l’appel récursifafficherAnnees(2021, 2022) - Les deux appels suivants
afficherAnnees(2021 2022)etafficherAnnees(2022, 2022)provoquent l’affichage de 2021 et 2022. - Noter que le code à la ligne 5 n’a toujours pas été exécuté.
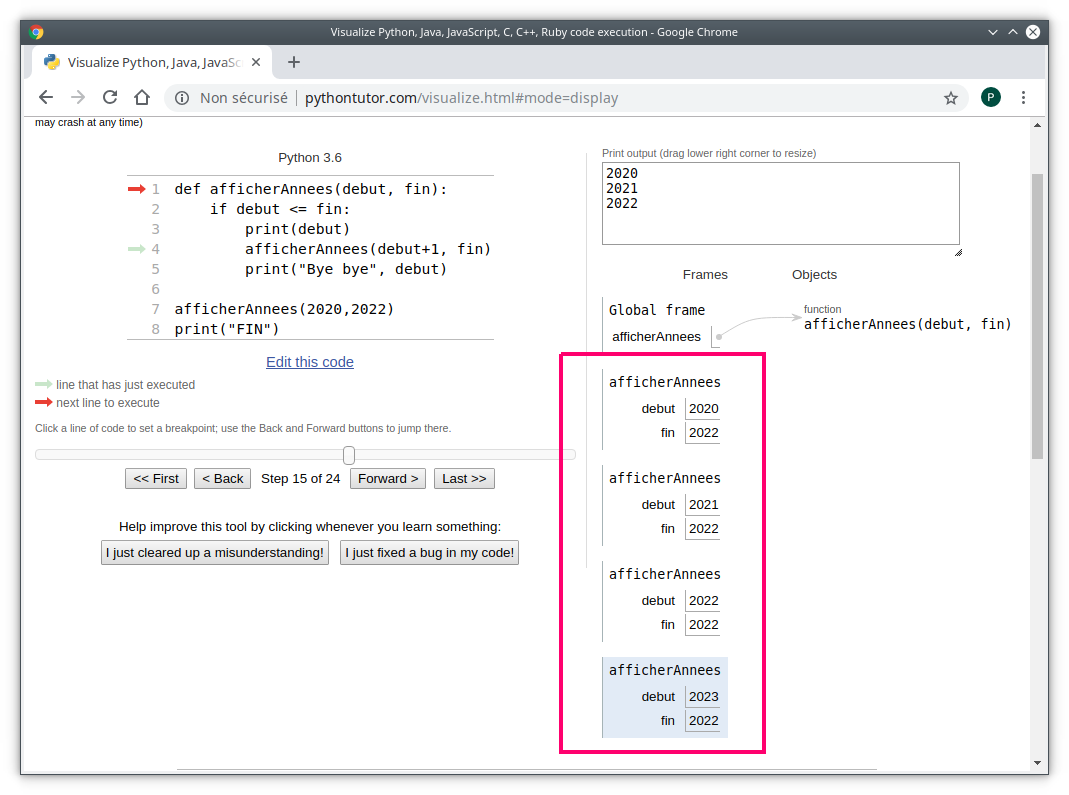
- Après l’appel
afficherAnnees(2022, 2022)l’appelafficherAnnees(2023, 2022)est lancé ; la pile des appels contients alors 4 appels qui s’empilent cf. image ci-dessous :
- Désormais, les appels vont dépiler puisque
2023 > 2022. - L’appel
afficherAnnees(2023, 2022)ne provoque aucun effet mais, en se terminant, il va débloquer l’appelafficherAnnees(2022, 2022)ce qui permet l’affichage deBye bye 2022. La pile des appels diminue d’une unité. - Chaque fin d’appel provoque alors le déblocage du code de la ligne 4 puis l’affichage
Bye bye .... - A la fin (ligne 8), la pile d’appels est vide.
La somme des \(n\) premiers entiers¶
L’exemple précédent est typique de la récursivité mais l’exemple qui suit va bien mettre en évidence ce qu’on appelle le cas de base et l’exemple nous montrera une difficulté que peut poser la récursivité.
Soit la fonction \(\mathtt{f}\) telle que, pour tout entier \(\mathtt{n\geq 1}\) on ait \(\mathtt{f(n) =1+2+\dots+n}\), somme des entiers entre 1 et \(\mathtt{n}\) inclus. Par exemple,
- \(\mathtt{f(3)=1+2+3=6}\),
- \(\mathtt{f(4)=1+2+3+4=10}\),
- \(\mathtt{f(10)=1+2+3+\dots+9+10=55}\).
On va implémenter la fonction \(\mathtt{f}\) dans une version récursive. La construction algorithmique de \(\mathtt{f}\) est basée sur l’observation suivante : pour connaître, par exemple, la somme \(\mathtt{S}\) des entiers de 1 à 4, il suffit de connaître la somme \(\mathtt{T}\) des entiers de 1 à 3 et dans ce cas \(\mathtt{S=T+4}\). Autrement dit
\(\mathtt{f(4)=f(3)+4}\)
ce qui n’est qu’un cas particulier de la relation suivante, valable pour \(\mathtt{n\geq 2}\) :
\(\mathtt{f(n) = f(n-1)+n }\)
Cette relation est appelée parfois relation de récurrence. Il est essentiel de noter que la relation précédente ne s’applique pas si \(\mathtt{n=1}\) puisque \(\mathtt{f(0)}\) n’a pas été définie. Toutefois, \(\mathtt{f(1)}\) existe et vaut 1.
Ci-dessous, voici un code qui implémente la fonction \(\mathtt{f}\) en Python en utilisant la relation ci-dessus :
1 2 3 4 5 6 7 8 9 | def f(n):
if n == 1:
return 1
else:
return f(n-1)+n
print(f(3))
print(f(4))
print(f(10))
|
10 11 12 | 6
10
55
|
- ligne 5 : la fonction
fs’appelle elle-même. - lignes 2-3 : c’est ce qu’on appelle le « cas de base » dans une récursion.
On notera que l’implémentation de \(\mathtt{f}\) suit exactement la relation de récurrence ci-dessus (cf. ligne 5 du code), y compris pour son cas d’exclusion (\(\mathtt{n=1}\), cf. lignes 2-3).
Enfin, il aurait été possible de définir la somme pour le cas de base \(\mathtt{n=0}\) en lui donnant 0 pour valeur (c’est la valeur conventionnelle attribuée à une somme vide) et en définissant la relation de récurrence \(\mathtt{f(n) = f(n-1)+n }\) pour \(\mathtt{n\geq 1.}\)
Limitation du nombre d’appels récursifs¶
Il existe de nombreuses situations algorithmiques où il est efficace d’utiliser une fonction récursive. Toutefois, les appels sont effectués sur une zone de mémoire plutôt limitée (dite stack alias la pile) et donc la pile d’appels ne doit pas dépasser une certaine limite. Par défaut, elle est de 1000 dans l’implémentation courante de Python. Sinon, on obtient une erreur :
1 2 3 4 5 6 7 8 | def f(n):
# Calcule 1+2+...+n
if n==0:
return 0
else:
return n+f(n-1)
print(f(1200))
|
qui affiche
1 | RuntimeError: maximum recursion depth exceeded in comparison
|
Remède¶
Le plafond de 1000 peut varier selon les réglages de Python. Par exemple, avec la version Jupyter-Notebook d’Anaconda, le plafond semble plutôt autour de 2000 appels récursifs.
En Python, il est possible de modifier le plafond du nombre d’appels :
1 2 3 4 5 6 7 8 9 10 11 | import sys
sys.setrecursionlimit(1500)
def f(n):
# Calcule 1+2+...+n
if n==0:
return 0
else:
return n+f(n-1)
print(f(1200))
|
12 | 720600
|
- Lignes 1-2 : la taille de la pile est augmentée à 1500 appels.
Depuis la version 3.5 de Python, une exception de type RecursionError est déclenchée en cas de dépassement de la limite.
Précaution¶
Toutefois, comme indiqué dans la documentation, pour des raisons de portabilité, on modifiera avec prudence le plafond des appels. En outre, même si on le lève, un crash peut se produire :
import sys
N=20000
sys.setrecursionlimit(N)
def f(n):
# Calcule 1+2+...+n
if n==0:
return 0
else:
return n+f(n-1)
print(f(N))
Erreur de segmentation (core dumped)
On remarquera que le crash est grave au point qu’il a échappé au système d’exceptions de Python.
Enfin, même en levant de façon raisonnable le plafond de la pile, le programme peut être plus lent que son équivalent itératif :
import sys
from time import perf_counter
N = 20000
sys.setrecursionlimit(N)
def it(n):
s = 0
for k in range(1, n + 1):
s += k
return s
def rec(n):
return n + rec(n - 1) if n else 0
def test(n, h):
begin_perf = perf_counter()
for i in range(1000):
h(N // 2)
print("%s : %.2fs" % (h.__name__, perf_counter() - begin_perf))
test(N / 2, rec)
test(N / 2, it)
rec : 3.89s
it : 0.38s
Ici, le code récursif est 10 fois plus lent.
Autre langages¶
Le problème rencontré est dû à un débordement de la pile des appels (un stack overflow en anglais) et se retrouve, à des degrés divers, dans de nombreux langages de programmation non fonctionnels (C/C++, Java, Javascript, etc).
Par exemple, en Java, le code suivant
1 2 3 4 5 6 7 8 9 10 11 12 13 | public class Somme {
public static void main(String[] args) {
System.out.println(somme(12000));
}
public static long somme(long n) {
if (n != 1)
return n + somme(n - 1);
return 1;
}
}
|
fait un stack overflow alors qu’il y a moins de 12000 appels (comme en Python, on pourrait augmenter la taille de la pile et améliorer le plafond).
En C++, le code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | #include<iostream>
using namespace std;
long long somme(long long n)
{
if (n==1)
return 1;
return n+somme(n-1);
}
int main()
{
cout<<somme(1000000000)<<endl;
return 0;
}
|
semble supporter un milliard d’appels (compilé avec -O2).
Pour un langage comme OCaml où la programmation récursive est courante, le stack overflow se produit, sur mon système, autour de 263000 appels si on compile en bytecode et autour de 530000 si on compile en code natif :
1 2 3 4 5 6 | let rec somme n =
if (n=1) then 1
else n + somme (n-1) ;;
print_int (somme 263000) ;;
print_newline () ;;
|
7 8 | $ ocaml s.ml
Stack overflow during evaluation (looping recursion?).
|
Ecrire un algorithme récursif¶
L’algorithme précédent montre bien les deux étapes d’un algorithme récursif. Pour écrire un algorithme récursif résolvant un problème X appliqué à un objet N, on dégage les deux éléments suivants :
- le sous-problème : on identifie le même problème que le problème \(\mathtt{X}\) mais appliqué à un objet \(\mathtt{M}\) de « taille » inférieure et dont la résolution permet de résoudre le problème \(\mathtt{X}\) appliqué à l’objet \(\mathtt{N}\)
- le cas de base : on isole le cas du problème X appliqué à un objet de taille telle que le problème pour X ne peut être ramené à un sous problème ; il s’agit en quelque sorte d’un cas irréductible.
Par exemple, dans le problème de la somme précédente, le problème \(\mathtt{X}\) est de calculer la somme \(\mathtt{S}\) des \(\mathtt{n}\) premiers entiers et l’objet N est l’entier strictement positif \(\mathtt{n}\); on se rend compte que pour connaître \(\mathtt{S}\), il suffit de savoir résoudre le même problème mais pour un objet plus petit, à savoir \(\mathtt{n-1}\) puisque si l’on connaît la somme \(\mathtt{T}\) des \(\mathtt{n-1}\) premiers entiers alors \(\mathtt{S=T+n}\). Cependant, la règle précédente ne s’applique que si on peut effectivement décomposer le problème ce qui suppose que \(\mathtt{n}\) vaut au moins 1 et ce qui fournit le cas de base.
Le problème de la terminaison de la récursion doit être examiné, même s’il est parfois délicat de la prouver, elle nécessite souvent de raisonner par récurrence voire par induction.
Placement du cas de base¶
Reprenons le calcul de la somme des \(n\) premiers entiers :
1 2 3 4 5 | def f(n):
if n == 1:
return 1
else:
return f(n-1)+n
|
Chaque appel commence par le test de la condition de terminaison (ligne 2). Si n = 100, le test va être négatif dans 99 cas et positif dans le dernier cas. Autant faire en sorte que le test soit positif le plus souvent possible. D’où le code suvant :
def f(n):
if n != 1:
return f(n-1)+n
else:
return 1
voire les code plus simples suivants :
def f(n):
if n != 1:
return f(n-1)+n
return 1
ou encore
def f(n):
return f(n-1)+n if n != 1 else 1
En pratique, cela ne change pas les temps d’exécution mais c’est plus logique [la remarque sur le placement du cas de base est suggérée ici].
Le saviez-vous ?¶
Dans certains environnements, l’usage de récursivité n’est pas permis.
- Dans le secteur du logiciel embarqué dans des véhicules (terrestres, aériens), certains principes d’implémentation d’unités logicielles découragent explicitement le recours à toute forme de récursion (directe ou indirecte), cf. le standard ISO 26262, ou encore le standard MISRA pour le langage C ainsi que la norme JSF-AV (avionique en C++).
- Les standards de codage de la NASA recommandent d’éviter toute forme de récursion, cela fait partie de la règle n°1, cf. The Power of Ten (pdf).
- En programmation CUDA, les fonctions qui s’exécutent sur le GPU (les kernels) ne peuvent être récursives, comme indiqué dans le guide 2020 de programmation CUDA C++.
- Dans des langages compilés comme C/C++ ou Java, le compilateur peut optimiser certains appels de fonctions en procédant à l’inlining du code de la fonction. Une fonction récursive aura un inlining qui sera limité.
Résolution de problèmes par des algorithmes récursifs¶
Certains problèmes sont définis de manière éminemment récursive ; voici quelques exemples :
- le tri rapide (quicksort)
- le tri fusion (mergesort)
- la recherche dichotomique dans une liste ordonnée
- l’évaluation des expressions algébriques
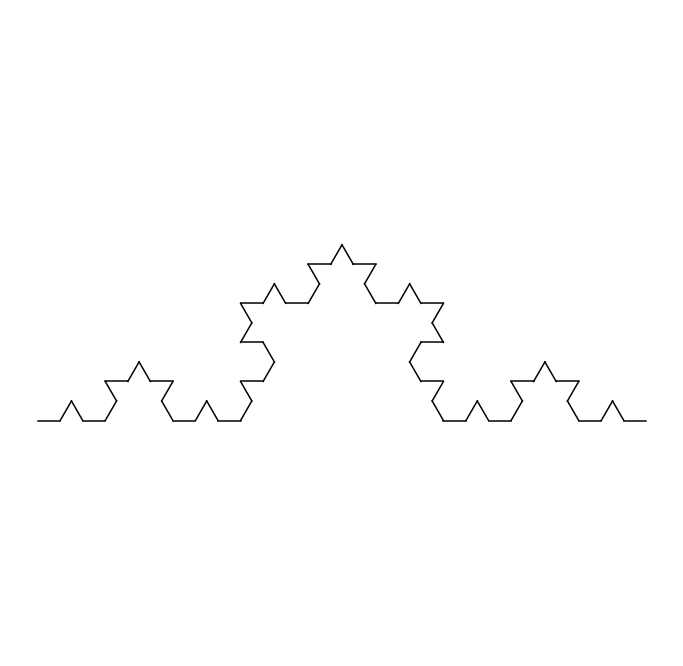
- tracé de certains fractals (courbes de Von Koch, éponge de Sierpinsky, etc)
- le parcours en profondeur dans un graphe
- l’algorithme de Karatsuba de multiplication de deux grands entiers
- les problèmes de convergence de suite du type \(x_{n+1}=f(x_n)\) comme la méthode de Newton.
Pour certains problèmes, qu’ils soient définis de manière récursive ou pas, l’algorithme de résolution peut être implémenté en version récursive ou en version itérative. C’est par exemple le cas :
- d’une recherche dichotomique,
- d’un parcours en profondeur,
- d’une conversion d’un entier en base 2,
- du calcul du pgcd par l’algorithme d’Euclide.
- de l’algorithme de transformée de Fourier rapide et discrète (en traitement du signal)
Le choix d’une version de l’algorithme plutôt que l’autre sera dicté par les facteurs suivants :
- la facilité de codage,
- les performances.
Dans certains cas, un algorithme récursif sera beaucoup plus concis que son équivalent itératif.
Enfin, itération et récursion ne sont pas antinomiques. Par exemple, de nombreux problèmes de combinatoire et de dénombrement utilisent des appels récursifs dans des structures itératives, cf. exercices.
GirafariG¶
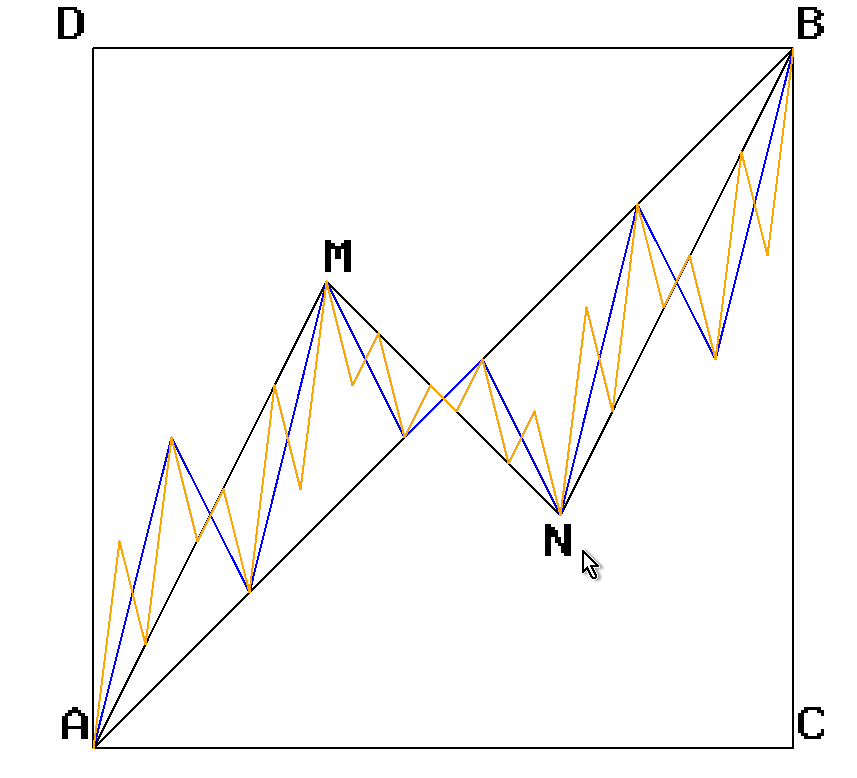
Un palindrome est une chaîne de caractères qui est identique lue de gauche à droite ou de droite à gauche. Par exemple, la chaîne GIRAFARIG est un palindrome : si on inverse le mot, il reste identique.
Pour coder récursivement un test de palindrome (cf. dessin ci-dessous), il suffit de vérifier que
- les lettres aux extrémités sont les mêmes (les lettres en bleu sur la figure);
- le mot privé de ses deux extrémités est encore un palindrome (en orange sur le dessin), d’où appel récursif.
Précaution : quand on vérifie que le mot privé de ses deux extrémités est encore un palindrome, il faut faire attention à ce que le retrait des extrémités soit possible. Ce problème ne se pose que si le mot a une lettre ou n’a aucune lettre. Dans ces cas, le mot est un palindrome, ce qui donne le cas de base de la récursivité. Remarquons que si le mot a deux lettres, ce n’est pas un cas de base car quand on lui retire ses extrémités, la chaîne devient vide et on tombe sur un cas de base.
On en déduit le code suivant :
1 2 3 4 5 6 7 | def estPalindrome(mot):
if len(mot)<=1:
return True
return mot[0]==mot[-1] and estPalindrome(mot[1:-1])
print(estPalindrome("girafarig"))
print(estPalindrome("girafariga"))
|
- Ligne 4 :
mot[1:-1]est un slice : c’est la chaînemotamputée de son premier caractère (elle commence à l’indice 1 et se termine juste avant l’indice -1, ce dernier indice référençant le dernier caractère de la chaîne).
C’est anecdotique mais on peut même simplifier le code :
def estPalindrome(mot):
return not mot or mot[0]==mot[-1] and estPalindrome(mot[1:-1])
Récursivité illustrée par la conversion en base b¶
Soit à déterminer la liste des chiffres de la représentation en base \(\mathtt{b}\) d’un entier \(\mathtt{n}\). Par exemple, si \(\mathtt{n=13}\) et \(\mathtt{b=2}\) alors les chiffres de la représentation de \(\mathtt{n}\) en base \(\mathtt{b}\) sont les éléments de la liste \(\mathtt{[1, 1, 0, 1]}\) puisque \(\mathtt{13=8+4+0+1}\). Autre exemple et qui permet de mieux comprendre : la liste des chiffres en base 10 de l’entier 2038 est [2, 0, 3, 8].
Je précise qu’ici les chiffres sont vus comme entiers entre 0 et \(b-1\) et non comme des caractères.
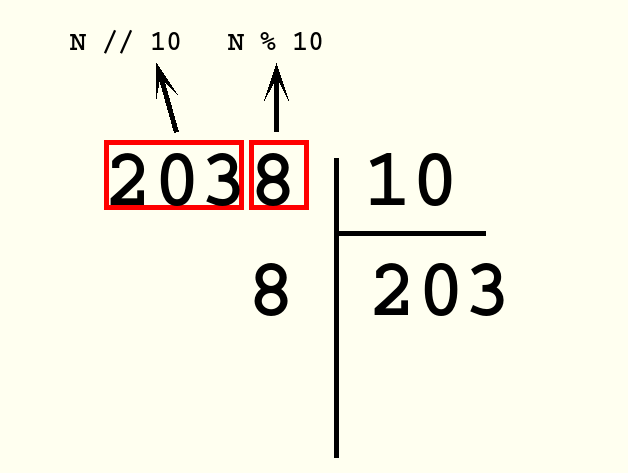
On cherche donc à écrire une fonction récursive chiffres(n, b) qui renvoie la liste des chiffres de n en base b. Pour cela essayons de voir comment on peut ramener la conversion de n en base b à la conversion d’un autre nombre. Reprenons l’exemple \(\mathtt{n=2038}\) et \(\mathtt{b=10}\) et effectuons la division entière de \(\mathtt{n}\) par \(\mathtt{b}\), comme illustrée sur la figure :
On observe alors que le reste \(\mathtt{r}\) n’est autre que le dernier chiffre de \(\mathtt{n}\) et que le quotient \(\mathtt{q}\) n’est autre que l’entier \(\mathtt{n}\) privé de son dernier chiffre. On peut donc reconstituer la liste des chiffres de \(\mathtt{n}\) à partir de celle de \(\mathtt{q}\) et de celle de \(\mathtt{r}\). Dans notre exemple, et avec la syntaxe Python des listes, on a [2, 0, 3, 8] = [2, 0, 3] + [8].
On en déduit le code (encore incomplet) suivant :
1 2 3 4 5 | def chiffres(n, b):
# Manque le cas de base
q = n // b
r = n % b
return chiffres(q, b) + [r]
|
Le cas de base se produit lorsqu’on ne peut pas priver \(\mathtt{n}\) de son dernier chiffre, autrement dit lorsque \(\mathtt{n}\) a un seul chiffre autrement dit lorsque \(\mathtt{n < b}\). Dans ce cas, la liste des chiffres est juste la liste [n].
On peut cette fois écrire le code complet :
1 2 3 4 5 6 7 8 9 10 | def chiffres(n, b):
if n < b :
return [n]
q = n // b
r = n % b
return chiffres(q, b) + [r]
print(2038, "->", chiffres(2038, 10))
print(5, "->", chiffres(5, 10))
print(13, "->", chiffres(13, 2))
|
11 12 13 | 2038 -> [2, 0, 3, 8]
5 -> [5]
13 -> [1, 1, 0, 1]
|
Récursivité illustrée par la recherche dichotomique¶
Etant donné une liste L d’objets triés par ordre croissant et un objet x, l’algorithme de recherche dichotomique (binary search en anglais) est un algorithme efficace de recherche de la présence de x dans la liste L.
Etude d’un exemple¶
Montrons sur un exemple le fonctionnement d’une recherche dichotomique. Le principe de base est qu’à chaque étape de l’algorithme, on va choisir la « bonne moitié » de la liste, celle où se trouve x.
Soit la liste croissante L = [12, 31, 46, 53, 81, 81, 82] et soit x = 42. On découpe la liste en les deux listes suivantes qui sont moitié moins grandes que la liste L :
[12, 31, 46] et [53, 81, 81, 82]
En comparant avec 46 (dernier terme de la première liste), on voit que x est forcément dans la première liste, disons M = [12, 31, 46].
On découpe à nouveau cette liste en les deux listes suivantes qui sont moitié moins grandes que la liste M :
[12] et [31, 46]
En comparant avec 12 (dernier terme de la première liste), on voit que x est forcément dans la deuxième liste [31, 46].
On découpe à nouveau cette liste en deux :
[31] et [46]
En comparant avec 31 (dernier terme de la première liste), on voit que x est forcément dans la deuxième liste [46]. Comme cette liste est de taille 1, il suffit de regarder si l’élément x = 42 est cet élément : ce n’est pas le cas, donc la liste initiale ne contient pas l’élément 42.
Principe de la recherche dichotomique¶
Le principe est le suivant : on découpe la liste en deux sous-listes de taille « environ » la moitié de la liste initiale (le « environ » est précisé ci-dessous) et on identifie la sous-liste M susceptible de contenir x et on recommence la même recherche dans cette nouvelle sous-liste.
Pour préciser le « environ » ci-dessus, si \(n\) est la taille de L le découpage par moitiés se fera suivant les longueurs définies par les décompositions ci-dessous :
- si \(n=2k\) est pair alors on décomposera en \(n=k+k\)
- si \(n=2k+1\) est pair alors on décomposera en \(n=k+(k+1)\)
et en particulier, on décide, conventionnellement, que la liste de gauche n’est jamais plus longue que celle de droite.
Noter que si les indices de L commencent à 0 alors, avec les notations \(n=2k\) ou \(n=2k+1\) ci-dessus, la longueur de la première sous-liste \(M\) du découpage est toujours \(k\) et donc l’indice \(i\) du dernier élément de \(M\) est k-1. Or, que \(n\) soit pair ou pas, \(k\) est le quotient de la division entière de \(n\) par 2 et donc, i = n//2 - 1 où // est la division entière.
Implémentation de la recherche dichotomique¶
De l’étude ci-dessus de la recherche dichotomique d’un élément x dans une liste croissante L, on peut déduire le code ci-dessous :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | def dicho(L,x):
n=len(L)
if n>1:
p=n//2-1
if x <= L[p]:
return dicho(L[:p+1], x)
else:
return dicho(L[p+1:], x)
return n==1 and L[0]==x
L = [12, 31, 46, 53, 81, 81, 82]
print(dicho(L, 42))
print(dicho(L, 80))
|
- Ligne 10 : cas où la liste
Lcontient un seul élément. - Lignes 3-8 : cas où la liste
Lcontient plus d’un élément. - Lignes 6 et 8 : on partage la liste en deux sous-listes, le première étant de longueur
n//2. - Ligne 4 : l’indice
pest le dernier indice de la première moitié. - Lignes 5-6 : si
x <= L[p]alorsxne peut être que dans la première sous-liste, c’est-à-direL[:p+1]qui est la liste de tous les éléments deLd’indice \(\mathtt{0\leq j< p+1}\) autrement dit \(\mathtt{0\leq j\leq p}\). D’où un appel récursif pour rechercherxdans cette sous-liste. - Lignes 7-8 : dans l’autre cas, on recherche récursivement
xdans la 2e sous-liste.
Compléments¶
Il faudrait faire davantage de tests, en testant tous les entiers entre par exemple 0 et 100 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | def dicho(L,x):
n=len(L)
if n>1:
p=n//2-1
if x <= L[p]:
return dicho(L[:p+1], x)
else:
return dicho(L[p+1:], x)
return n==1 and L[0]==x
L = [12, 31, 46, 53, 81, 81, 82]
for x in range(100):
wrong = dicho(L, x) != (x in L)
if wrong:
break
if not wrong:
print("TEST OK")
else:
print("TEST KO")
|
L’implémentation de dicho a juste pour objectif d’illustrer la récursivité appliquée à la dichotomie. En pratique, ce n’est pas ainsi (en utilisant des slices) qu’une dichotomie est implémentée. En outre, quand on fait une dichotomie, on souhaite pouvoir encadrer l’élément à chercher avec les éléments de la liste.
En réalité, une recherche dichotomique est un algorithme tellement basique qu’il est implémenté dans la majorité des bibliothèques standard des langages. Pour Python, le module standard bisect implémente (en langage C) la recherche dichotomique dont on peut lire un code source Python au lien suivant : bisect.py.
Récursivité inefficace¶
Soit le fameux triangle de Pascal :
Chaque coefficient, dit coefficient binomial, s’obtient en faisant la somme des deux coefficients qui sont au-dessus et à gauche, par exemple (ligne numérotée 7 dans la figure) : \(35 = 20 + 15\).
Chaque coefficient est indexé par son numéro de ligne et son numéro de colonne. L’usage est de faire commencer les indices à 0. Par exemple, le coefficient 35 est à l’indice de ligne 7 et l’indice de colonne 4.
On cherche à écrire une fonction pascal(n,p) qui renvoie le coefficient situé à la ligne d’indice n et à la colonne d’indice p, par exemple n (dernière ligne), pascal(10, 6) = 210. Donc, d’après la propriété du tableau de Pascal, on a la relation
\(\mathtt{pascal(n, p) = pascal(n-1, p) + pascal (n-1, p-1)}\)
Précision¶
On peut étendre la définition de la fonction pascal(n,p) si \(\mathtt{p > n}\) en lui donnant la valeur 0, puisque pascal(n,p) vaut aussi \(\mathtt{n\choose p}\) qui est le nombre de façons de choisir \(\mathtt{p}\) objets parmi \(\mathtt{n}\). Toutefois cette extension ne sera pas implémentée dans les codes ci-dessous.
L’algorithme itératif¶
On peut en déduire un algorithme itératif :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | def ligne_suivante(L):
LL=[]
LL.append(1)
n=len(L)
for k in range(1, n):
LL.append(L[k-1]+L[k])
LL.append(1)
return LL
def pascal_it(n,p):
L=[1, 1]
for i in range(0, n-1):
LL=ligne_suivante(L)
L=LL
return L[p]
pascal(1000,200)
|
- Lignes 1-8 : à partir d’une ligne du tableau de Pascal, on construit la suivante en appliquant la propriété du tableau de Pascal (une ligne du tableau est une liste).
- Lignes 10-15 : on génère toutes les lignes du tableau de Pascal jusqu’à la ligne d’indice
net on lit l’élément d’indicepde la liste. - Ligne 17 : on obtient le résultat (une nombre de 216 chiffres) presque instantanément.
L’algorithme récursif¶
Revenons à la formule :
\(\mathtt{pascal(n, p) = pascal(n-1, p) + pascal (n-1, p-1)}\)
Elle donne aussi le schéma d’une fonction récursive pascal(n, p) pour calculer chaque coefficient du tableau de Pascal :
1 2 3 | def pascal(n, p):
# ! Code encore incomplet !
return pascal(n-1, p) + pascal (n-1, p-1)
|
Il faut simplement faire attention aux cas de base. La relation ci-dessus est vraie si le coefficient n’est pas à l’extrémité d’une ligne d’une tableau, ie si \(\mathtt{0< p <n}\). Dans ces autres cas, \(\mathtt{pascal(n, p)}\) vaut 1 [je rappelle que le cas \(\mathtt{p > n}\) n’est pas implémenté].
D’où le code Python suivant :
1 2 3 4 5 6 | def pascal(n, p):
if 0 < p < n:
return pascal(n-1, p)+pascal(n-1,p-1)
return 1
print(pascal(10,6))
|
7 | 210
|
Simple ! n’est-ce pas ?
Pourtant, l’exécution va se montrer très lente. Le calcul de pascal(30,14) pourra mettre jusqu’à une minute :
1 2 3 4 5 6 7 8 9 10 11 | from time import time
def pascal(n, p):
if 0 < p < n:
return pascal(n-1, p)+pascal(n-1,p-1)
return 1
debut = time()
print(pascal(30,14))
duree=time()-debut
print(int(duree), "secondes")
|
12 13 | 145422675
61 secondes
|
ce qui est énorme pour un résultat aussi simple.
Recomptages multiples¶
Comment expliquer ce phénomène ? Il n’est pas dû à débordement de la pile d’appel car pascal(30,14) engendre une pile d’au plus 30 appels, on est loin de la limite.
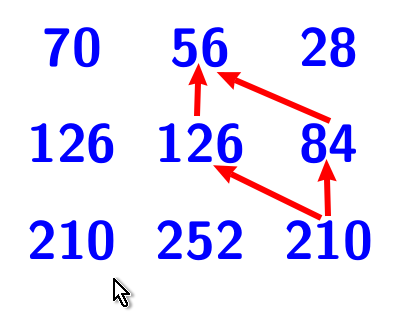
Pour comprendre, regardons comment s’effectue le calcul de, par exemple, pascal(10,6) comme le montre le dessin ci-dessous :
On a pascal(10, 6) = pascal(9, 5) + pascal(9, 6) ie 210 = 126 + 84. Le calcul de pascal(9, 5) = 126 va nécessiter le calcul de pascal(8, 5) = 56. Une fois le calcul de pascal(9, 5)= 126 effectué, l’algorithme récursif va calculer pascal(9, 6) = 126. Et ce dernier va nécessiter le calcul de pascal(8, 5). Et pourtant, l’algorithme a déjà calculé cette valeur lors du calcul de 126 = pascal(9, 5).
Et plus on considère des positions hautes dans le tableau plus les valeurs à ces positions seront recalculées par la fonction pascal. D’ailleurs, en modifiant l’algorithme ci-dessus, on peut calculer le nombre d’appels de la fonction, en plaçant un compteur qui s’incrémente à chaque appel :
1 2 3 4 5 6 7 8 9 10 | def pascal(n, p):
global cpt
cpt+=1
if p==0 or p==n:
return 1
return pascal(n-1, p)+pascal(n-1,p-1)
cpt=0
print(pascal(30,14))
print(cpt, "appels")
|
11 12 | 145422675
290845349 appels
|
On voit qu’il y a eu presque 300 millions d’appels alors que pascal(30, 14) ne nécessite, en théorie, que la connaissance de quelques dizaines de valeurs du tableau de Pascal !
En définitive, on se rend compte que notre algorithme a un problème de mémoire : il passe son temps à calculer des valeurs qu’il a déjà calculées mais qu’il n’a pas « notées ». L’algorithme itératif n’a pas ce problème, il retient chaque ligne du tableau de Pascal.
Complément : du poisson dans notre algorithme¶
Pour remédier à ce problème de défaillance mnésique, on va donner un peu de mémoire à notre algorithme tout en lui conservant son caractère récursif. Pour cela, on va utiliser un dictionnaire dont les clés seront les couples (n, p) ce qui donne le code suivant :
1 2 3 4 5 6 7 8 9 10 11 12 | def pascal(n, p):
if (n, p) in memoire:
return memoire[n,p]
if 0 < p < n:
v = pascal(n-1, p)+pascal(n-1,p-1)
else:
v=1
memoire[n, p]=v
return v
memoire={}
print(pascal(30,14))
|
13 | 145422675
|
- Ligne 11 : on définit un dictionnaire
memoireinitialement vide. - Ligne 8 : chaque fois que la fonction
pascal(n, p)calcule le coefficient, le résultat est mémorisé dans le dictionnaire. - Lignes 2-3 : chaque fois que la fonction
pascal(n, p)est appelée, pour éviter un recalcul, on commence par si le tuple(n, p)est dans le dictionnaire, et s’il y est, on récupère sans recalcul la valeurpascal(n, p).
L’exécution de pascal(30,14) est alors instantanée et aussi rapide qu’avec la méthode itérative.
Le cas de la suite de Fibonacci¶
Pour illustrer l’inefficacité de certaines récursions, il est courant d’évoquer la suite de Fibonacci. Il s’agit d’une suite d’entiers telle que les deux premiers termes sont 1 et encore 1 et, chaque terme de la suite à partir du troisième s’obtient en faisant la somme des deux précédents.
Voici les 12 premiers termes de la suite de Fibonacci :
\(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144\)
et, par exemple, ci-dessus, \(89 = 34 + 55\).
La définition même de la suite de Fibonacci suggère un algorithme récursif immédiat de calcul du \(n\)-ème de la suite :
1 2 3 4 5 | def fibo(n):
if n >2:
return fibo(n-1)+fibo(n-2)
return 1
print(f(41))
|
6 | 165580141
|
Toutefois, le calcul est très long, par exemple le calcul de f(41) peut nécessiter jusqu’à une minute alors qu’une version itérative fournit instantanément le résultat. Le problème est exactement le même que pour le triangle de Pascal : une croissance exponentielle du nombre d’appels récursifs par défaut de mémorisation.
La différence avec le triangle de Pascal est qu’il est assez simple de modifier fibo pour garder une fonction récursive mais qui soit efficace. Il suffit de donner un peu de mémoire à la fonction en plaçant dans ses arguments deux termes consécutifs de la suite de Fibonacci. D’où le code :
1 2 3 4 5 6 | def fibo(n, a, b):
if n==0:
return a
return fibo(n-1, b, a+b)
print(fibo(41,0, 1))
|
7 | 165580141
|
qui calcule le \(n\)-ème terme de la suite et qui, cette fois, s’exécute instantanément.
Pour comprendre comment fonctionne ce code, il suffit d’observer l’évolution des arguments lors des appels successifs :
1 2 3 4 5 6 7 | def fibo(n, a, b):
print(a, b)
if n==0:
return a
return fibo(n-1, b, a+b)
fibo(12,0, 1)
|
0 1
1 1
1 2
2 3
3 5
5 8
8 13
13 21
21 34
34 55
55 89
89 144
144 233
On voit qu’il s’agit, à chaque appel, de deux termes consécutifs de la suite, si bien qu’on comprend qu’au bout de n étapes, l’un d’entre eux soit le terme recherché.
Qu’est-ce qu’on mange ?¶
On considère les repas que l’on peut composer partir
- d’une liste des entrées
- d’une liste des plats principaux
- d’une liste des desserts
Voici donc la « carte »:
| Entrée | Plat | Dessert |
| guacamole | poulet | mousse |
| quiche | saumon | tarte |
| omelette | glace |
Quelle est la liste de tous les repas possibles ? Pour cela, il suffit de choisir une entrée parmi 2, puis pour chaque entrée, un plat principal parmi 3 (ce qui fait 6 choix possibles au total) et pour chacun de ces choix, un des 3 desserts possibles ce qui fait au total \(\mathtt{6\times 3=18}\) menus possibles.
Il s’agit mathématiquement de construire le produit cartésien \(\mathtt{E\times P\times D}\) des trois ensembles
\(\mathtt{E=\{guacamole, quiche\}}\), \(\mathtt{P=\{poulet, saumon, omelette\}}\) et \(\mathtt{D=\{mousse, tarte, glace\}}\),
autrement dit l’ensemble des triplets de la forme \(\mathtt{(entrée, plat, dessert)}\).
Codage naïf¶
Bien sûr, il est possible d’imbriquer des boucles for pour répondre à la question initiale :
1 2 3 4 5 6 7 8 | entrees = ["guacamole", "quiche"]
plats =["poulet", "saumon", "omelette"]
desserts = ["mousse","tarte", "glace"]
for e in entrees:
for p in plats:
for d in desserts:
print(e, p, d)
|
qui affiche
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | guacamole poulet mousse
guacamole poulet tarte
guacamole poulet glace
guacamole saumon mousse
guacamole saumon tarte
guacamole saumon glace
guacamole omelette mousse
guacamole omelette tarte
guacamole omelette glace
quiche poulet mousse
quiche poulet tarte
quiche poulet glace
quiche saumon mousse
quiche saumon tarte
quiche saumon glace
quiche omelette mousse
quiche omelette tarte
quiche omelette glace
|
Mais le code ne fonctionne que pour 3 étapes dans le repas et pas pour un nombre d’étapes quelconque (s’il y a 10 étapes il faut récrire le code et 10 boucles imbriquées …).
Fonction récursive¶
On va coder une fonction récursive menu(etapes) où etapes est une liste des \(\mathtt{p}\) étapes d’un repas, chaque étape étant elle-même une liste, par exemple
desserts = ["mousse","tarte", "glace"].
Il existe un algorithme récursif répondant à la question. Voyons sur un exemple comment se fait l’appel récursif. Supposons que l’on dispose sous forme d’une liste M de tous les menus possibles à partir des étapes entrées, plats et desserts et que l’on veuille compléter le menu avec le choix d’un élément dans une liste de fruits. Pour composer la liste R de tous les repas possibles, il faut et il suffit de considérer tous les menus m dans M et compléter la liste m par n’importe quel fruit possible.
Pour le cas de base qui correspond à \(\mathtt{p=1}\) alors la liste cherchée n’est autre que \(\mathtt{[L[0]]}\) où \(\mathtt{L[0]}\) est l’unique liste.
Concernant le code, il est important de comprendre que la fonction menus(etapes) renvoie une liste de tous les repas possibles et qu’un repas est lui-même une liste constituée d’un item de chaque étape du repas. D’où le code suivant :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | def menus(etapes):
n=len(etapes)
if n==1:
return [[choix] for choix in etapes[0]]
M=menus(etapes[:n-1])
E=etapes[-1]
R=[]
for m in M:
for choix in E:
R.append(m+[choix])
return R
entrees = ["guacamole", "quiche"]
plats =["poulet", "saumon", "omelette"]
desserts = ["mousse","tarte", "glace"]
etapes=[entrees, plats, desserts]
repas=menus(etapes)
for r in repas:
print(*r)
|
guacamole poulet mousse
guacamole poulet tarte
guacamole poulet glace
guacamole saumon mousse
guacamole saumon tarte
guacamole saumon glace
guacamole omelette mousse
guacamole omelette tarte
guacamole omelette glace
quiche poulet mousse
quiche poulet tarte
quiche poulet glace
quiche saumon mousse
quiche saumon tarte
quiche saumon glace
quiche omelette mousse
quiche omelette tarte
quiche omelette glace
- Lignes 6-11 : pour le cas qui n’est pas de base, on génère (récursivement, ligne 6) la liste
Mde tous les menus que l’on peut composer en ignorant la dernière étape du repas, comme le montre le sliceetapes[:n-1]. - Lignes 9-11 : pour chaque menu possible
mprovenant deM, on complète le menu par un choix fourni par la dernière étape du repas. - Ligne 11 : le repas est une liste, voilà pourquoi on lit
[choix]. - Lignes 8-11 : en complétant de toutes les manières possibles, on obtient tous les repas possibles sous forme d’une liste
R.
Complément¶
Rien à voir avec la récursivité, mais le module standard itertools permet de générer automatiquement les menus possibles :
from itertools import product
entrees = ["salade", "tomates"]
plats =["steak", "saumon", "omelette"]
desserts = ["yaourt","flan", "gâteau"]
menus = product(entrees, plats, desserts)
for m in menus:
print(*m)
Arbre de Pythagore¶
On se propose de dessiner la figure fractale suivante (vous devriez distinguer clairement un arbre) :
La figure ci-dessus est un arbre de Pythagore de longueur 9.
Un arbre de longueur \(n\geq 1\) se construit à l’aide d’un tronc (1 carré) surmonté de deux arbres de longueur \(n-1\), l’un à gauche l’autre à droite.
Un arbre de hauteur 1 est constitué uniquement du tronc.
Voici un arbre de Pythagore de hauteur 3 :
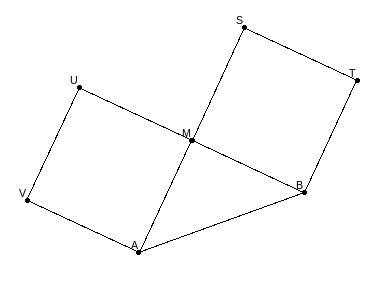
Un arbre (disons \(T\)) de hauteur \(\mathtt{n>0}\) sera construit à l’aide d’une fonction récursive \(\texttt{arbre(A,B,C,D,n)}\) où \(\texttt{ABCD}\) représente le tronc de \(T\) (\(\texttt{A}\) en haut à gauche, \(\texttt{B}\) en haut à droite) et où \(\texttt{n}\) désigne la hauteur de \(T\).
Pour simplifier le codage, on fournit le code suivant :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | def gauche(A, B):
a, b=A
c,d=B
M=(1/2*a + 1/2*b + 1/2*c - 1/2*d,
-1/2*a + 1/2*b + 1/2*c + 1/2*d)
U=(a + b - d, -a + b + c)
V=(3/2*a + 1/2*b - 1/2*c - 1/2*d,
-1/2*a + 3/2*b + 1/2*c - 1/2*d)
return M, U, V
def droite(A,B):
a, b=A
c,d=B
M=(1/2*a + 1/2*b + 1/2*c - 1/2*d,
-1/2*a + 1/2*b + 1/2*c + 1/2*d)
S=(b + c - d, -a + c + d)
T=(-1/2*a + 1/2*b + 3/2*c - 1/2*d,
-1/2*a - 1/2*b + 1/2*c + 3/2*d)
return M, S, T
from turtle import *
hideturtle()
up()
O=(0,0)
A=(200,0)
B=(100,100)
begin_fill()
goto(O)
goto(A)
goto(B)
goto(O)
end_fill()
exitonclick()
|
On y lit deux fonctions \(\texttt{gauche(A, B)}\) et \(\texttt{droite(A,B)}\) qui à partir d’un tronc dont la base supérieure est le segment AB (A à gauche et B à droite) renvoie les coordonnées des trois nouveaux points M, U et V de la branche gauche et de même pour la branche droite (M, S et T), cf. le dessin ci-dessous :
Le code ci-dessus explique aussi la syntaxe Turtle pour remplir de noir un polygone (avec les commandes \(\texttt{begin\_fill()}\) et \(\texttt{end\_fill()}\)).
Fonction remplir¶
Pour noircir les éléments carrés de l’arbre,
on a besoin d’une fonction remplir(x, y, z, t) où x, y, z et t sont des sommets du carrés (donc des points de la forme (a, b)) :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | from turtle import *
hideturtle()
up()
def remplir(x,y,z,t):
begin_fill()
goto(x)
goto(y)
goto(z)
goto(t)
goto(x)
end_fill()
u=100
O=(0,0)
A=(u,0)
B=(u,-u)
C=(0,-u)
remplir(O,A,B,C)
exitonclick()
|
- Lignes 7-11 : on dessine le contour du carré
- Lignes 6 et 12 : on encadre le contour de deux instructions de remplissage.
La fonction récursive¶
Soit à dessiner un arbre (disons \(T\)) de hauteur \(\mathtt{n\geq 1}\), de tronc ABCD où A et B sont les points de la partie supérieure du tronc, là où vont pousser les branches. Cet arbre va être dessiné par une fonction récursive arbre(A, B, C, D, n).
Supposons \(\mathtt{n\geq 2}\). La fonction doit
- dessiner le tronc ABCD
- faire pousseur deux arbres sur ce tronc, l’un à gauche (disons \(T_1\)), l’autre à droite (disons \(T_2\)).
Pour faire pousser \(T_1\), la fonction arbre fera un appel récursif. De même pour \(T_2\). Il reste à déterminer les arguments des appels récursifs.
Pour construire \(T_1\), il faut connaître son tronc AMUV. On connaît un sommet du tronc (le sommet A qui est un paramètre). Les autres sommets seront obtenus avec une fonction gauche(A, B). De même, le tronc BMST de \(T_2\) sera déterminé par une fonction droite(A, B).
Finalement, une fois les sommets des troncs trouvés, il faut :
- appeler
arbre(V, U, n-1)pour dessiner les branches au-dessus du tronc AMUV - appeler
arbre(S, T, n-1)pour dessiner les branches au-dessus du tronc BMST.
On a écrit n-1 car, le tronc de \(T\) étant dessiné (hauteur 1), il reste des arbres \(T_1\) et \(T_2\) de longueur n-1 à faire pousser.
Lorsque \(\mathtt{n=1}\), arbre(A, B, C, D, n) dessinera juste le tronc ABCD.
D’où le code suivant :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | def gauche(A, B):
a,b=A
c,d=B
M=(1/2*a + 1/2*b + 1/2*c - 1/2*d, -1/2*a + 1/2*b + 1/2*c + 1/2*d)
U=(a + b - d, -a + b + c)
V=(3/2*a + 1/2*b - 1/2*c - 1/2*d, -1/2*a + 3/2*b + 1/2*c - 1/2*d)
return M, U, V
def droite(A,B):
a,b=A
c,d=B
M=(1/2*a + 1/2*b + 1/2*c - 1/2*d, -1/2*a + 1/2*b + 1/2*c + 1/2*d)
S=(b + c - d, -a + c + d)
T=(-1/2*a + 1/2*b + 3/2*c - 1/2*d, -1/2*a - 1/2*b + 1/2*c + 3/2*d)
return M, S, T
from turtle import *
hideturtle()
up()
def remplir(x,y,z,t):
begin_fill()
goto(x)
goto(y)
goto(z)
goto(t)
goto(x)
end_fill()
def arbre(A, B, C, D, n):
remplir(A, B, C, D)
if n>1:
M,U,V=gauche(A,B)
M,S,T=droite(A,B)
arbre(V, U, M, A, n-1)
arbre(S, T, B, M, n-1)
speed(0)
d=100
A=(0,0)
B=(d,0)
C=(d,-d)
D=(0,-d)
n=5
arbre(A, B, C, D, 0)
mainloop()
|
Compléments : version en couleur¶
On va rajouter de la couleur à l’arbre. Le tronc initial sera dessiné couleur chocolat et les feuilles finales seront couleur verte. Les couleurs intermédiaires proviendront d’un gradient.
Le gradient est déterminé, composante RGB par composante RGB, de manière proportionnelle entre la composante de la couleur initiale et la couleur finale.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 | from turtle import *
CHOCO=("d2", "69", "1e")
GREEN=("00", "ff", "00")
def fade(a, b, n):
if n==1:
return [a]
h=(b-a)/(n-1)
r=[]
for k in range(n):
v=hex(round(a+k*h))[2:]
if len(v)==1:
v="0"+v
r.append(v)
return r
def gradient(rgbA, rgbB, n=10):
Ar, Ag, Ab=[int(z, base=16) for z in rgbA]
Br, Bg, Bb=[int(z, base=16) for z in rgbB]
r=fade(Ar, Br, n)
g=fade(Ag, Bg, n)
b=fade(Ab, Bb, n)
return ["#"+''.join(z) for z in list(zip(r,g,b))][::-1]
def gauche(A, B):
a,b=A
c,d=B
M=(1/2*a + 1/2*b + 1/2*c - 1/2*d, -1/2*a + 1/2*b + 1/2*c + 1/2*d)
U=(a + b - d, -a + b + c)
V=(3/2*a + 1/2*b - 1/2*c - 1/2*d, -1/2*a + 3/2*b + 1/2*c - 1/2*d)
return M, U, V
def droite(A,B):
a,b=A
c,d=B
M=(1/2*a + 1/2*b + 1/2*c - 1/2*d, -1/2*a + 1/2*b + 1/2*c + 1/2*d)
S=(b + c - d, -a + c + d)
T=(-1/2*a + 1/2*b + 3/2*c - 1/2*d, -1/2*a - 1/2*b + 1/2*c + 3/2*d)
return M, S, T
def remplir(x,y,z,t, col="#000000"):
fillcolor(col)
begin_fill()
goto(x)
goto(y)
goto(z)
goto(t)
goto(x)
end_fill()
def arbre(A, B, C, D, n, colors):
remplir(A, B, C, D, colors[n])
if n>1:
M,U,V=gauche(A,B)
M,S,T=droite(A,B)
arbre(V, U, M, A, n-1, colors)
arbre(S, T, B, M, n-1, colors)
def go(n):
colors=gradient(CHOCO, GREEN, n)
hideturtle()
up()
speed(0)
d=100
A=(0,0)
B=(d,0)
C=(d,-d)
D=(0,-d)
arbre(A, B, C, D, 8, colors)
mainloop()
go(n=9)
|
Récursivité illustrée par le tri rapide¶
Les algorithmes du type « diviser pour régner », comme la recherche dichotomique, utilisent souvent, de par leur nature, des fonctions récursives. C’est le cas de l’algorithme du quicksort (tri rapide en français).
Voici son principe de fonctionnement. On se donne une liste L, par exemple d’entiers, que l’on veut trier dans l’ordre croissant, par exemple la liste suivante :
L = [21, 14, 19, 18, 36, 35, 21, 15, 16, 42, 13, 33, 12]
Le tris se fait en trois étapes :
- partitionnement
- tri à gauche
- tri à droite
D’abord, on isole un élément arbitraire de la liste, en pratique ce sera le premier élément de la liste à trier, dans notre exemple, c’est 21. Cet élément, disons p, est appelé le pivot. Ensuite, on écarte provisoirement le pivot de sa position et on se débrouille pour placer
- en début de liste tous les éléments \(\mathtt{x}\) de la liste tels que \(\mathtt{x\leq p}\)
- en fin de liste tous les éléments \(\mathtt{x}\) de la liste tels que \(\mathtt{p < x}\)
- dans la case restante, on place le pivot
p.
Cette étape s’appelle le partitionnement suivant le pivot.
Par exemple, dans la liste L ci-dessus, les éléments suivants :
14, 19, 18, 21, 15, 16, 13, 12
sont déplacés dans la partie gauche de la liste L ;
les éléments restants :
33, 42, 35, 36
sont déplacés dans la partie droite de la liste L ;
Il reste alors une case vide et on y place le pivot, en sorte que la nouvelle liste L est :
L = [14, 19, 18, 21, 15, 16, 13, 12, 21, 33, 42, 35, 36].
On constate que les éléments à gauche du pivot étant plus petits que le pivot, ils resteront du côté gauche une fois la liste L triée. De même, pour les éléments à droite du pivot. Donc,
- le pivot est à sa place définitive
- si on trie le sous-tableau
Lgà gauche du pivot et si on trie le sous-tableauLddes éléments à droite du pivot, alors la listeLsera complètement triée.
Toute la subtilité du quicksort réside dans le fait que Lg et Ld vont être triés par la méthode du quicksort et donc avec deux appels récursifs (qui représentent les deux dernières étapes).
Restent à traiter les cas de base : ils apparaissent lorsque le partitionnement n’a pas de sens, c’est-à-dire lorsque la liste L est vide.
Pour présenter l’algorithme et à des fins pédagogiques, le partitionnement se fera dans un tableau auxiliaire. En pratique, les implémentations n’utilisent jamais de tableaux auxiliaires car cela nuirait gravement aux performances du tri, qui comme son nom l’indique, doit rester rapide.
D’où le code suivant et dont le seul but est d’illustrer la récursivité et pas d’implémenter de manière efficace un quicksort :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | def quicksort(L):
n=len(L)
if n==0:
return []
pivot=L[0]
gauche=[x for x in L[1:] if x <= pivot]
droite=[x for x in L[1:] if pivot < x]
tri_gauche = quicksort(gauche)
tri_droite = quicksort(droite)
return tri_gauche + [pivot] + tri_droite
L=[21, 14, 19, 18, 36, 35, 21, 15, 16, 42, 13, 33, 12]
print(quicksort(L))
print(L)
|
15 16 | [12, 13, 14, 15, 16, 18, 19, 21, 21, 33, 35, 36, 42]
[21, 14, 19, 18, 36, 35, 21, 15, 16, 42, 13, 33, 12]
|
- Lignes 3-4 : le cas de base : la liste est vide. Si la liste contient un seul élément, elle est partitionnée en deux listes entourant le pivot, ce qui ramène au cas de base.
- Ligne 5 : on nomme le pivot
- Ligne 6 ou 7 : les éléments de la liste autres que le pivot sont dans le slice
L[1:] - Ligne 6 : on place dans la liste
gauchetous les éléments inférieurs ou égaux au pivot (y compris donc un doublon du pivot) ; - Ligne 7 : on place dans la liste
droitetous les éléments strictement supérieurs au pivot. - Ligne 8 : on trie la liste
gauchepar un appel récursif àquicksort - Ligne 9 : on trie la liste
droitepar un appel récursif àquicksort - Ligne 10 : on place le pivot seul dans une liste entre les deux listes triées précédentes et on concatène les trois listes ce qui retourne la liste définitivement triée.
- Lignes 12 et 16 : la liste initiale n’est pas modifiée et c’est une copie de
Lqui est triée.
Complément : oneliner¶
Il est même possible d’écrire le corps de la fonction quicksort sur une seule ligne (logique) :
1 2 3 4 5 6 7 8 | def quicksort(L):
return (quicksort([z for z in L if z<L[0]]) +
[z for z in L if z==L[0]] +
quicksort([z for z in L if z>L[0]])
if L else [])
L=[21, 14, 19, 18, 36, 35, 21, 15, 16, 42, 13, 33, 12]
print(quicksort(L))
|
9 | [12, 13, 14, 15, 16, 18, 19, 21, 21, 33, 35, 36, 42]
|
Récursif ou itératif ?¶
Comment choisir entre une implémentation récursive et une implémentation itérative d’un même algorithme ? La récursivité s’exprime souvent très simplement : un algorithme ayant une définition récursive s’implémentera naturellement de façon récursive. C’est le cas par exemple pour le tri rapide ou le tri fusion qui s’implémentent la plupart du temps récursivement.
Toutefois, dans des langages tels que C, C++, Python, Rust où un appel de fonction peut avoir un coût non négligeable, la récursivité peut engendrer une pénalisation. Par ailleurs, la récursivité peut entraîner une saturation de la pile. Donc, sauf contexte particulier, d’apprentissage par exemple, on évitera d’utiliser un code récursif engendrant un nombre d’appels en \(\mathtt{O(n)}\) où \(\mathtt{n}\) est la valeur traitée et on pourra envisager de l’utiliser si le nombre d’appels est un \(\mathtt{O(\log n)}\) ou si on est certain de ne traiter que de petites instances ou si on dispose pas d’alternative itérative. Typiquement, si on est soucieux de performance, on évitera de calculer un maximum ou une somme récursivement.
De même, en théorie des graphes, on évitera de lancer récursivement un parcours en profondeur (DFS) ; d’ailleurs, les DFS des bibliothèques comme
implémentent itérativement.
De même, la méthode de Newton de résolution d’équation \(f(x)=0\) ou des algorithmes d’approximations successives comme la descente de gradient seront écrits itérativement.
Et même lorsque le nombre d’appels récursifs est de l’ordre de \(\mathtt{O(\log n)}\), il se peut que les implémentations dominantes soient itératives. Voici trois exemples :
- l’algorithme classique de Transformée de Fourier rapide, dont la définition est récursive ; les implémentations sont traditionnellement itératives.
- la recherche dichotomique est souvent écrite itérativement ;
- l’algorithme d’Euclide de calcul du pgcd ainsi que la version optimisée de CPython écrite en C (cf. la fonction
_PyLong_GCD) sont itératives, ce qui peut se comprendre puisque Python peut utiliser des entiers de très grande taille (plusieurs centaines ou milliers de chiffres) et que la complexité de l’algorithme est de l’ordre du nombre de chiffres du diviseur.
1. Maximum de trois entiers en récursif¶
(Exercice assez factice de récursivité) Ecrire une fonction récursive max(a, b, c) qui renvoie le maximum de trois entiers a, b et c. On se ramènera à un calcul d’un maximum de la forme max(x, y, y).
2. Fonction ensureRange¶
(Exercice assez factice de récursivité) On donne trois nombres a, b et x. On demande d’écrire une fonction récursive ensureRange(a, b, x) valant l’élément le plus proche de x situé dans l’intervalle d’extrémités a et b. Voici quelques exemples de comportements :
a = 0, b = 5, x = 2 -> 2
a = 5, b = 0, x = 2 -> 2
a = 0, b = 5, x = 5 -> 5
a = 5, b = 0, x = 5 -> 5
a = 0, b = 5, x = 6 -> 5
a = 5, b = 0, x = 6 -> 5
a = 0, b = 5, x = -1 -> 0
a = 5, b = 0, x = -1 -> 0
a = 0, b = 0, x = 5 -> 0
a = 0, b = 0, x = -1 -> 0
a = 0, b = 0, x = 0 -> 0
3. Nombre intermédiaire entre trois entiers¶
(Exercice assez factice de récursivité) Ecrire une fonction récursive interm(a, b, c) qui renvoie un entier parmi a, b et c qui est encadré par les deux autres. Par exemple interm(3, 1, 2) = 2 ou encore interm(1, 3, 1) = 1.
4. Dis « Bonjour ! »¶
Ecrire une fonction récursive bonjour(n) qui affiche sur des lignes différentes n fois le message Bonjour ! où n est un entier positif ou nul.
5. Plus petit entier se terminant par 42¶
On se donne un entier n, par exemple n=2030, et on cherche le plus petit entier supérieur à n et qui se termine par 42. Si n=2030 alors la réponse attendue est 2042. Le recherche se fera sous la forme f(n) où f sera une fonction récursive n’employant aucune forme de boucle.
Remarquer qu’un entier n se termine par 42 si et seulement si le reste de sa division par 100 est justement 42.
6. Tours de Hanoï¶
On dispose de 3 tiges verticales A, B et C et de \(\mathtt{n \geq 0}\) disques percés en leur centre, de diamètres strictement croissants, empilés sur la tige A et disposés en sorte que chaque disque repose sur un disque de diamètre strictement supérieur :
Le problème des tours de Hanoï est de translater cette pile sur la tige C
par une succession de déplacements de disques d’une tige à une autre (on a besoin de la tige B), un seul disque à la fois, mais avec la contrainte qu’au cours des déplacements de disques, on ne pose jamais un disque sur un disque de diamètre strictement inférieur.
Ecrire une fonction récursive hanoi(n, source, but, aux) qui prend en entrée
- le nombre
nde disques à déplacer - le nom de la tige où se trouvent les disques à déplacer (
source) - le nom de la tige de destination finale des
ndisques (but) - le nom de la troisième tige et qui va servir de tige auxiliaire ou temporaire pour réaliser les déplacements (
aux).
La fonction hanoi ne renvoie rien mais affiche chaque déplacement de disque à effectuer (le nom de la tige de départ et de la tige d’arrivée) afin de mouvoir tous les disques depuis leur position initiale (source) à leur position finale (but).
Par exemple, si l’appel est hanoi(3, "A", "C", "B") alors le programme pourra afficher :
A C
A B
C B
A C
B A
B C
A C
ce qui signifie que
- le disque au sommet de la tige A est déplacé sur la tige C
- le disque au sommet de la tige A est déplacé sur la tige B
- le disque au sommet de la tige C est déplacé sur la tige B
- etc.
Le schéma ci-dessous aide à comprendre comment la fonction récursive doit être écrite :
Quelques explications au schéma : pour déplacer les 9 disques de la tige A vers la tige C, il y a trois étapes :
- on déplace (par appel récursif) les 8 disques supérieurs (un disque de moins que ce qu’il y a au départ) vers la tige provisoire B,
- on déplace le disque restant de la tige A vers sa position finale, la tige C,
- par appel récursif, on déplace les 8 disques de la tige B vers la tige C.
Le point important à comprendre est que pour réaliser tout déplacement d’une pile de n + 1 disques entre une tige de départ et une tige d’arrivée, il suffit de savoir comment déplacer toute pile de n disques (un de moins) d’une tige à une autre.
7. Puissance récursive¶
Écrire une fonction récursive power(a, m) qui calcule \(\mathtt{a^m}\) où \(\mathtt{a}\) est un nombre et \(\mathtt{m}\) un entier positif ou nul. Tester. Naturellement, il est exclu d’utiliser toute opération du type x ** n mais cela pourra servir à vérifier ses tests.
8. Puissance récursive d’un nombre complexe¶
Étant donné un entier naturel \(\mathtt{n\geq 0}\) et un nombre complexe \(\mathtt{z}\) écrit sous forme algébrique \(\mathtt{z=x+iy}\) où \(\mathtt{x, y\in\mathbb{R}}\), on demande de calculer les parties réelle et imaginaire du nombre complexe \(\mathtt{z^n}\). On écrira une fonction récursive cpow(x, y, n) qui renverra les parties réelle et imaginaire de \(\mathtt{(x+iy)^n}\). Python permet de calculer avec de véritables nombres complexes mais on utlisera pas cette possibilités, on travaillera uniquement avec des nombres réels.
Par exemple, l’appel cpow(-2, 1, 5) doit renvoyer le couple (38, 41) ce qui traduit que \(\mathtt{(-2+i)^5=38+41 i}\) ce que l’on peut vérifier avec Python par le calcul suivant :
z = -2 + 1j
print(z**5)
(38+41j)
Pour construire la fonction récursive, on écrira tout simplement que \(\mathtt{z^{n-1}=z^{n-1}\times z}\) et le membre de droite sera calculé en faisant le produit de deux nombres complexes.
9. Le premier chiffre¶
L’entier 2030 commence par 2, l’entier \(\mathtt{1999}\) commence par 1, l’entier 42 commence par 4.
Ecrire une fonction récursive premier_chiffre(n) qui reçoit un entier \(\mathtt{n \geq 0}\) et qui renvoie le nombre valant le premier chiffre de l’écriture de n en base 10.
On appliquera la technique d’extraction employée dans le cours pour convertir un entier en base b.
10. Somme des chiffres d’un entier¶
Ecrire une fonction récursive somme_chiffres(n) qui renvoie la somme des chiffres en base 10 de l’entier \(\mathtt{n\geq 0}\).
Exemple de comportements :
0 → 0
1 → 1
8 → 8
42 → 6
2024 → 8
100000000000000000000 → 1
On décomposera \(\mathtt{n}\) entre son chiffre des unités (n%10) et ses autres chiffres, obtenus par n//10, cf. la technique employée dans le cours pour convertir un entier en base b.
11. Sommes partielles de la série harmoniques¶
Soit la série harmonique
\(H_n=\ds\frac 11+\frac 12+\frac 13+\cdots \frac 1n\)
Par exemple, le 3e terme de la série harmonique est \(H_3=1+1/2+1/3 =11/6\). On remarquera que chaque terme de la suite s’obtient aisément à l’aide du précédent. Ecrire une fonction récursive harm(n) qui renvoie la liste des \(n\) premiers termes de la série harmonique.
Par exemple harm(3)=[1, 3/2, 11/6].
Pour manipuler des fractions en Python, on utilisera le module fractions :
>>> from fractions import Fraction
>>> q = Fraction(11, 6)
>>> print(q)
11/6
>>>
Voici un exemple d’éxécution du code :
from fractions import Fraction
def harm(n):
# votre code ICI
H10 = harm(10)
print(*map(str, H10), sep=', ')
et qui affiche :
1, 3/2, 11/6, 25/12, 137/60, 49/20, 363/140, 761/280, 7129/2520, 7381/2520
12. Développement égyptien¶
Une fraction égyptienne est une fraction du type \(\ds\frac 1n\) où \(n\) est un entier strictement positif. On peut démontrer que tout rationnel strictement positif \(r=\ds\frac ab\) peut s’écrire comme somme de fractions égyptiennes ayant des dénominateurs tous différents et on dira alors que cette somme est un « développement égyptien » de \(r\). Un développement égyptien n’est pas unique. Il existe, par ailleurs, plusieurs algorithmes de génération d’une décomposition, voir par exemple le document de David Eppstein.
Décrivons un algorithme simple de décomposition. Soit à déterminer un développement égyptien de \(r=\ds\frac ab\) où \(a\) et \(b\) sont des entiers et \(a>1\). Alors, l’identité
\(\ds \frac ab =\frac 1b + \frac{a-1}{b+1} + \frac{a-1}{b(b+1)}\)
fournit un algorithme récursif de détermination d’un développement égyptien : l’algorithme se termine (le numérateur \(a-1\) diminue) et les dénominateurs sont distincts (l’idée étant que l’application \(x>0\mapsto x(x+1)\) est injective).
On demande d’écrire une fonction récursive dev_egypt(a, b) qui renvoie une liste des dénominateurs des fractions du développement égyptien que fournit l’algorithme ci-dessus.
Par exemple, dev_egypt(3, 7) renvoie [7, 8, 9, 72, 56, 57, 3192] et on peut vérifier que
\(\ds\frac 37=\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\frac{1}{72}+\frac{1}{56}+\frac{1}{57}+\frac{1}{3192}\)
13. Somme de la somme de la … des chiffres¶
Soit un entier \(\mathtt{N\geq 1}\). On note \(\mathtt{s(N)}\) la somme de la somme etc des chiffres de \(\mathtt{N}\), les sommes étant calculées tant que le résultat est un entier ayant au moins deux chiffres. Par exemple, si \(\mathtt{N=49538}\) alors la somme des chiffres de \(\mathtt{N}\) est 29. Comme cette somme a deux chiffres, on recommence et on obtient \(\mathtt{2+9=11}\) et comme ce résultat est encore à deux chiffres, on continue pour obtenir finalement \(\mathtt{s(N)=2}\).
On se donne deux entiers \(\mathtt{k, n\geq 1}\), on demande d’écrire une fonction récursive srec(n, k) qui calcule \(\mathtt{s(N)}\) où \(\mathtt{N}\) est l’entier composé de \(\mathtt{k}\) blocs de chiffres égaux à ceux de \(\mathtt{n}\). Par exemple, \(\mathtt{srec(49538, 3)}\) vaut \(\mathtt{s(495384953849538)}\).
Pour calculer la somme des chiffres d’un entier on pourra utiliser la méthode suivante :
n=49538
S=sum(int(z) for z in str(n))
print(S)
29
Cet exercice provient de HackerRank : Recursive Digit Sum.
La somme est également répertoriée sur le site EOIS sous la dénomination de Digital root.
14. Plus long préfixe commun¶
On donne deux listes L et M d’entiers et on demande d’écrire une fonction récursive prefixe(L, M) qui renvoie la sous-liste P qui soit à la fois :
- commune à
LetM, - commençant au début de chaque liste,
- la plus longue possible.
Voici quelques exemples de comportements :
L = [0, 5, 8, 6, 4, 7, 2]
M = [0, 5, 8, 9, 4, 7, 2, 4]
P = [0, 5, 8]
----------------
L = [0, 5, 8, 6, 4, 7, 2]
M = [0, 5, 8, 6, 4, 7, 2, 4]
P = [0, 5, 8, 6, 4, 7, 2]
----------------
L = [0, 5, 8, 6, 4, 7, 2]
M = [1, 5, 8, 6, 4, 7, 2, 4]
P = []
----------------
15. Quotient illimité¶
On donne trois entiers \(\mathtt{a, b, n>0}\) avec \(\mathtt{a<b}\) et on demande d’écrire une fonction récursive quo_dec(a, b, n) qui renvoie la liste L des chiffres du quotient de \(\mathtt{a}\) par \(\mathtt{b}\) avec \(\mathtt{n}\) décimales. Par exemple, si \(\mathtt{a=1}\) et \(\mathtt{b=7}\) et \(\mathtt{n=20}\) on obtiendra que L vaut :
[1, 4, 2, 8, 5, 7, 1, 4, 2, 8, 5, 7, 1, 4, 2, 8, 5, 7, 1, 4]
Pour obtenir les décimales, on appliquera la méthode vue en classe de 6e, voir par exemple Pratique avec DÉCIMALES pour vous rafraîchir la mémoire.
En déduire une fonction div_dec(a, b, n) où \(\mathtt{a, b, n>0}\) sont des entiers qui renvoie la liste L des chiffres du quotient de \(\mathtt{a}\) par \(\mathtt{b}\) avec \(\mathtt{n}\) décimales. Par exemple, si \(\mathtt{a=22}\) et \(\mathtt{b=7}\) et \(\mathtt{n=20}\) on obtiendra que L vaut :
[3, 1, 4, 2, 8, 5, 7, 1, 4, 2, 8, 5, 7, 1, 4, 2, 8, 5, 7, 1, 4]
Application¶
On donne les entiers suivants :
a=1076825233969550892368765865908909828003038267654921050616858441627304937095412
b=342764117664681504901177527623702904503014768549643256761838650532817379076979
et on admet que \(\mathtt{\frac ab}\) a ses 156 premières décimales communes avec \(\pi\). Afficher la valeur approchée correspondante. On pourra utiliser la fonction list2digits ci-dessous pour obtenir un affichage lisible :
def list2digits(L):
return str(L[0]) + ',' + ''.join(map(str,L[1:]))
L=[3, 1, 4, 2, 8, 5, 7, 1, 4, 2, 8, 5, 7, 1, 4, 2, 8, 5, 7, 1, 4]
print( list2digits(L))
3,14285714285714285714
16. Multiplication du paysan russe¶
La multiplication dite « du paysan russe » ramène une multiplication de deux entiers naturels à une suite d’additions ou de divisions par 2. En voici une illustation à travers le produit \(\mathtt{85\times 18 = 1530}\) :
Cette multiplication est basée sur la propriété suivante : si \(\mathtt{a,b\in\N}\) alors
\(\mathtt{a\times b=\begin{cases}0 & \text{si } \mathtt{a} = 0\\\mathtt{a/2\times 2b}& \text{si } \mathtt{a} \text{ est pair et non nul}\\\mathtt{(a-1)\times b +b} & \text{sinon}\end{cases}}\)
Dans l’illustration ci-dessus, la 3e colonne est remplie lorsque a est impair.
Ecrire une fonction récursive paysan(a, b) qui implémente la multiplication ci-dessus. Tester en choisissant des entiers aléatoires.
17. De l’incrémentation à la puissance¶
Cet exercice est inspiré de Clang’s optimizer is ridiculously smart. Les entiers considérés ci-dessous seront positifs ou nuls. On demande d’écrire des fonction récursives.
- Implémenter l’addition par une suite d’incrémentations (d’une unité). Ainsi calculer \(5+3\) s’obtient en incrémentant d’une unité la somme \(5+2\).
- Implémenter la multiplication par une suite d’additions. Ainsi calculer \(10\times 6\) s’obtient en additionnant \(6\) au produit \(9\times 6\).
- Implémenter la puissance par une suite de multiplications. Ainsi, calculer \(3^7\) s’obtient en multipliant \(3^6\) par \(3\).
18. Méthode square and multiply¶
Ecrire une fonction récursive
power(a, n)qui renvoie \(\mathtt{a^n}\) en appliquant la méthode square and multiply qui consiste à ne faire que des successions d’élévation au carré ou de multiplication. Cette méthode consiste à remarquer que \(\mathtt{a^{2k}=(a^k)^2}\) et \(\mathtt{a^{2k+1}=a(a^k)^2}\).Par exemple, pour calculer \(\mathtt{x=10^{36}}\), on calculera \(\mathtt{y=10^{18}}\) puis \(\mathtt{y^2}\) ; et pour calculer \(\mathtt{y=10^{18}}\), on calculera \(\mathtt{z=10^9}\) puis \(\mathtt{y=z^2}\) ; pour calculer \(\mathtt{z=10^9}\), on remarquera que \(\mathtt{9=2\times 4+1}\) et donc on calculera \(\mathtt{u=10^4}\) et on obtiendra \(\mathtt{z= 10\times u^2}\) ; et ainsi de suite.
Modifier le code de la fonction pour qu’on puisse connaître le nombre de produits effectués. Combien faut-il de produits pour calculer \(\mathtt{10^{2048}}\) ?
19. I*N*S*E*R*E*R un astérisque¶
Ecrire une fonction récursive prenant en paramètre un mot formé de caractères alphabétiques et renvoyant le même mot mais dont les lettres sont séparées par des astérisques. Par exemple, si le mot initial est python, le mot à produire est p*y*t*h*o*n. On utilisera des slices à deux indices.
Cet exercice provient d’une question posée sur le forum Python d’OpenClassroom
20. Jeu du plus/moins¶
On veut simuler le jeu du plus/moins : vous devez découvrir un entier secret entre 1 et 100 milliards et, pour cela, vous avez la possibilité de proposer autant de fois que possible un entier choix à une fonction disMoi(choix), qui connaît le nombre secret et qui vous répond :
- le nombre
-1(ie c’est moins) si le nombre secret est strictement inférieur àchoix, - le nombre
1(ie c’est plus) si le nombre secret est strictement supérieur àchoix, - le nombre
0(ie bravo, c’est gagné !) si le nombre secret est égal àchoix.
Ecrire une fonction récursive deviner(inf, sup) qui doit renvoyer le nombre secret, sachant qu’il est compris, au sens large, entre les entier inf et sup. Le nombre secret sera le résultat de deviner(1, 100_000_000). Le code aura l’allure suivante :
from random import randrange
N=100_000_000
def jouer():
secret=randrange(N+1)
print(secret)
def disMoi(choix):
if secret < choix:
return -1
if secret > choix:
return 1
return 0
return disMoi
def deviner(inf, sup):
# Votre code récursif ICI
disMoi = jouer()
print(deviner(0, N))
Exemple de partie :
22595266
22595266
Cet exercice est directement inspiré du problème Leetcode : Guess Number Higher or Lower.
21. Etre une puissance de 2¶
Les puissances de 2 sont les entiers de la forme \(\mathtt{2^k}\) où \(\mathtt{k\geq 0}\) est un entier ; les premières puissances de 2 sont :
\(\mathtt{1\quad 2\quad 4\quad 8\quad 16\quad 32\quad 64\quad 128\quad 256}\)
Construire une fonction récursive estPuissance2(n) qui renvoie True si n (entier strictement positif) est une puissance de 2 et False sinon. Par exemple estPuissance2(2048) vaut True et estPuissance2(2024) vaut False
Indications pour construire la fonction récursive estPuissance2(n) :
- si
nest impair et différent de \(\mathtt{1}\) alors la fonction renvoie False - si
nest pair raisonner à l’aide de l’entier \(\mathtt{m}\) tel que \(\mathtt{n=2m}\).
22. Puissance de 2 \(\times\) nombre impair¶
Tout entier \(\mathtt{N}> 0\) peut s’écrire de manière unique comme un produit \(\mathtt{N=2^nd}\) d’une puissance de deux et d’un nombre impair \(\mathtt{d}\). Par exemple, \(\mathtt{2064}\) s’écrit : \(\mathtt{2064=2^4\times 129}\) donc pour 2064, on a \(\mathtt{n=4}\) et \(\mathtt{d=129}\).
On rappelle que \(\mathtt{1=2^0}\) est une puissance de \(\mathtt{2}\).
Écrire une fonction récursive \(\texttt{decomp(N)}\) qui renvoie la liste \(\mathtt{[2^n, d]}\). On trouvera quelques indications ci-dessous.
Voici quelques exemples de résultats attendus :
2064 -> [16, 129]
2029 -> [1, 2029]
64 -> [64, 1]
Indications pour construire la fonction récursive \(\texttt{decomp(N)}\) :
- le calcul de \(\texttt{decomp(N)}\) est facile si \(\texttt{N}\) est impair ;
- si \(\texttt{N}\) est pair, le calcul de \(\texttt{decomp(N)}\) se ramène à celui de la moitié de \(\texttt{N}\).
Votre fonction doit pouvoir traiter un nombre entier jusqu’à des milliersde chiffres.
23. Etre un carré parfait¶
On dit qu’un entier \(z\) est un carré parfait s’il existe un entier \(y\) tel que \(y^2=z\). Par exemple, 100 est un carré parfait puisque \(10^2=100\) mais \(42\) n’est pas un carré parfait.
On donne un entier \(\mathtt{a>0}\) et on demande d’écrire une fonction récursive estCarre et qui dira si, oui ou non, a est un carré parfait. La fonction aura la signature suivante : estCarre(a, mini, maxi) où mini est un minorant de la racine carrée de a et maxi est un majorant de la racine carrée de a. On encadrera alors la racine carrée par dichotomie. On lancera la recherche par estCarre(a, 1, a).
Tester pour les entiers suivants :
1578295627912817004054213311931596612284156721762423872790965280184834522246889
1982816527257334209808869577157761718909124662429638965435953370389693781
24. Plus petit diviseur, factorisation¶
Tout entier \(\mathtt{n>1}\) admet un plus petit diviseur autre que 1 que j’appelerai « le plus petit diviseur » de \(\mathtt{n}\). Par exemple,
- le plus petit diviseur de 42 est 2 ;
- le plus petit diviseur de 43 est 43 ;
- le plus petit diviseur de 49 est 7 ;
- le plus petit diviseur de 1000019 est 47.
Ecrire une fonction récursive
plus_petit_diviseur(n, d)qui renvoie le plus petit diviseur de \(\mathtt{n}\) et qui soit au moins égal à \(\mathtt{d}\). Par exemple,plus_petit_diviseur(45, 4)vaut 5.Cette fonction résout la question du plus petit diviseur de \(\mathtt{n}\) puisque celui-ci n’est autre que
plus_petit_diviseur(n, 2).Dans un premier temps, écrire une fonction qui soit capable de traiter tous les entiers \(\mathtt{n}\) jusqu’à 1000. L’idée est qu’on teste tous les \(\mathtt{d}\) possibles à partir de 2 et jusqu’à obtention.
Dans un 2e temps, pour pouvoir passer la barre des 1000 appels récursifs et pouvoir traiter des entiers de l’ordre de 1 million, on utilisera les résultats suivants :
- le seul diviseur de \(\mathtt{n}\) qui soit strictement supérieur à \(\mathtt{\sqrt n}\) est \(\mathtt{n}\) lui même ;
- si le nombre \(\mathtt{n}\) est impair, son plus petit diviseur est parmi 3, 5, 7, 9, 11, etc (cela va de deux en deux à partir de 3).
Déterminer le plus petit diviseur de 2053351.
En déduire une fonction récursive
factoriser(n)qui renvoie la liste des facteurs premiers de \(\mathtt{n\geq 2}\). Par exemple,factoriser(269500)est la liste[2, 2, 5, 5, 5, 7, 7, 11]. Factorisern=718512839393861635200000000000.Pour résoudre facilement cette question, il importe de remarquer que le plus petit diviseur de
nest un facteur premier den.
25. Répunits¶
Un entier positif u est dit un répunit si son écriture en base 10 n’est formée que de chiffres valant 1. Par exemple, cent onze est un répunit mais 42 n’est pas un répunit. Le nom répunit provient de la contraction des mots anglais REPeat et UNIT.
- Ecrire une fonction récursive
est_repunit(u)qui teste si un entier positifuest un répunit. Par exemple,est_repunit(0)etest_repunit(42)doivent renvoyerFalseetest_repunit(111)doit renvoyerTrue - Ecrire une fonction
repunit(n)qui renvoie le répunit ayantnchiffres. Par exemple,repunit(3)doit renvoyer l’entier 111.
26. Le logarithme itéré¶
Cet exercice est plus pour la culture générale que la récursivité !
Le logarithme itéré est une fonction qui sert à mesurer la complexité de certains algorithmes. Suivant la définition de Wikipedia, cette fonction, notée ci-après logstar est telle que logstar(n) est le plus petit nombre d’itérations du logarithme en base 2 initiées à n et qui donne une valeur inférieure ou égale à 1.
Par exemple, logstar(2020) vaut 4 comme le montrent les 4 itérations ci-dessous :
# Utilise Python 3.6
from math import log2
n=2020
it1=log2(n)
print(f"{it1:.2f}")
it2=log2(it1)
print(f"{it2:.2f}")
it3=log2(it2)
print(f"{it3:.2f}")
it4=log2(it3)
print(f"{it4:.2f}")
# FIN car résultat <= 1
10.98
3.46
1.79
0.84
Ecrire une implémentation récursive de la fonction logstar. Calculer logstar(n) pour \(\mathtt{n=2^{65537}}\).
27. Concaténer des entiers consécutifs¶
Ecrire une fonction récursive
nc(n)qui renvoie le nombre de chiffres (décimaux) de l’entiern. Par exemple,nc(2020)vaut 4.Si on écrit côte-à-côte tous les entiers entre 1 et
n = 42, on obtient le très grand entierNsuivant :123456789101112131415161718192021222324252627282930313233343536373839404142
On peut vérifier que
Nest un entier composé de \(\mathtt{p=75}\) chiffres. Ce qui peut se calculer de la manière suivante :- pour les entiers entre 1 et 9 : 9 chiffres
- pour les entiers entre 10 et 42 : \(\mathtt{(42-10+1)\times 2=66}\) chiffres
d’où le total de \(\mathtt{9+66=75}\) chiffres.
Plus généralement, étant donné un entier \(\mathtt{n\geq 1}\), on place côte-à-côte tous les entiers entre 1 et \(\mathtt{n}\) ce qui construit un très grand entier \(\mathtt{N}\). Ecrire une fonction récursive
concat_chiffres(n)qui renvoie le nombre \(\mathtt{p}\) de chiffres de \(\mathtt{N}\). Par exemple,concat_chiffres(2030)vaudra 7013. La fonctionconcat_chiffres(n)doit pouvoir s’exécuter pour des valeurs dentrès grandes ayant des dizaines de chiffres.L’algorithme récursif pourra être basé sur le calcul utilisé dans l’exemple pour déterminer
concat_chiffres(42). On pourra écrire une fonction récursive auxiliairef(k)qui calcule le nombre de chiffres quand on concatène tous les entiers- ayant exactement
kchiffres (le nombre de chiffres du concaténé s’obtient facilement puisque tous les entiers ont même nombre de chiffres) - ayant strictement moins de
kchiffres (le nombre de chiffres du concaténé s’obtient par appell récursif)
Par exemple, on trouvera que \(\mathtt{f(1)=9}\) ou \(\mathtt{f(2)=189}\).
Cette famille de nombres est enregistrée dans la base de suites d’entiers OEIS.
28. Combien de fois 42 ?¶
On donne un entier positif z et on définit combien42(z) comme étant le nombre de fois qu’on rencontre 42 dans l’écriture décimale de z. Par exemple,
combien42(52426423)vaut 2 ;combien42(2042)vaut 1 ;combien42(2024)vaut 0 ;
Donner un code récursif de la fonction combien42.
29. Entiers de Hamming¶
Un entier n>0 est dit de Hamming s’il peut s’écrire comme le produit d’une puissance de 2, d’une puissance de 3 et d’une puissance de 5. Par exemple, 5400 est un entier de Hamming car \(\mathtt{5400=2^3\times 3^3\times 5^2}\). De même, \(\mathtt{1=2^0}\) ou encore \(\mathtt{10}\) sont des nombres de Hamming. En revanche, 42 n’est pas un entier de Hamming.
Ecrire une fonction récursive is_hamming(n) qui renvoie True si n est un entier de Hamming et False sinon. Le programme doit pouvoir traiter des entiers de plusieurs dizaines de chiffres.
30. Diviser par deux ou retirer 1 (version récursive)¶
Observez le motif ci-dessous formé de 10 entiers. On part d’un entier \(a\geq 0\), ici \(a=81\), et on construit une suite d’entiers ainsi :
81 80 40 20 10 5 4 2 1 0
Le procédé de construction est défini ainsi : le successeur d’un entier \(x\) de la suite est la moitié de \(x\) si \(x\) est pair et sinon, ce successeur est \(x-1\). La suite se termine dès qu’un élément de la suite vaut 0.
Par exemple, dans la suite ci-dessus, le successeur de 80 est 40 car 80 est pair et que sa moitié est 40, et de même le successeur de 5 est 4 car 5 est impair et que \(4=5-1\).
On vous donne un entier \(a\geq 0\) et on vous demande d’afficher la suite générée à partir de \(a\) et de calculer la longueur de la suite ainsi générée. Par exemple, si \(a=79\) vous devez afficher la suite suivante :
79 78 39 38 19 18 9 8 4 2 1 0
et la longueur à calculer est de 12.
Vous utiliserez une fonction récursive. Vous pouvez éventuellement écrire aussi une fonction utilisant une boucle while pour vérifier la correction de votre fonction récursive.
La suite des longueurs est répertoriée sur le site de suites OEIS mais définie autrement.
31. Couplage de Cantor¶
[Exercice peut-être classique et que j’ai vu dans le très bon cours de Jean-Pierre Becirspahic : chapitre 2, exercice 4]
Le couplage de Cantor consiste à numéroter la grille des éléments de \(\n\times \n\) en 0, 1, 2, 3, …, comme le montre le dessin ci-dessous :
Par exemple, le couple \((2, 6)\) en colonne d’indice 2 et ligne d’indice 6 est numéroté 42. Au cas où le schéma ci-dessus ne se suffirait pas à lui-même, la numéroration commence en \(\mathtt{(0,0)}\) et s’effectue suivant des diagonales orientées sud-est vers nord-ouest. Arrivée sur la colonne la plus à gauche, la numérotation se poursuit sur la diagonale montante suivante en commençant par la ligne inférieure de la grille.
- Ecrire une fonction récursive
nro2point(nro)qui partant d’un numéro entier \(\mathtt{nro\geq 0}\) renvoie les coordonnées du points numéroté par \(\mathtt{nro}\). Par exemple,nro2point(42)est le couple(2,6). - Ecrire une fonction récursive
point2nro(point)qui partant d’un point \(\mathtt{point=(x,y)\in\n\times\n}\) renvoie le numéro depoint. Par exemple,point2nro((2,6))vaut 42.
32. Couplage de Cantor : variante¶
Une variante du couplage de Cantor consiste à numéroter la grille des éléments de \(\n\times \n\) en 0, 1, 2, 3, …, comme le montre le dessin ci-dessous :
Par exemple, le couple \((6, 2)\) en colonne d’indice 6 et ligne d’indice 2 est numéroté 42. Lorqu’une diagonale montante de la numérotation parvient à un point \(M\) de la colonne la plus à gauche, elle se poursuit avec le point \(N\) de la grille qui est immédiatement au-dessus de \(M\) et continue sur la diagonale descendante contenant \(N\). Arrivée en un point \(P\) de la ligne inférieure de la grille, la numérotation se poursuit avec le point \(Q\) immédiatement à droite de \(P\) et se poursuit sur la diagonale montante contenant \(Q\), et ainsi de suite.
Pour la suite, il pourra être utile de trouver un critère de distinction des diagonales montantes par rapport aux diagonales descendantes.
- Ecrire une fonction récursive
nro2point(nro)qui partant d’un numéro entier \(\mathtt{nro\geq 0}\) renvoie les coordonnées du points numéroté par \(\mathtt{nro}\). Par exemple,nro2point(42)est le couple(6,2). - Ecrire une fonction récursive
point2nro(point)qui partant d’un point \(\mathtt{point=(x,y)\in\n\times\n}\) renvoie le numéro depoint. Par exemple,point2nro((6,2))vaut 42.
33. Problème des \(n\) dames¶
On demande de coder récursivement le problème des n dames sur un échiquier (en français, le terme à utiliser est bien dames et pas reines) : il s’agit de placer n dames sur un échiquier de taille n x n sans qu’aucune d’entre elles ne puisse en prendre une autre, sachant qu’une dame à une position donnée peut prendre une pièce dans toute la colonne, la ligne ou les diagonales où elle est placée. Plus précisément, on cherche tous les placements possibles des n dames sur le plateau.
Voici une des 92 solutions lorsque n = 8 :
Chaque ligne et chaque colonne est indexée par un indice de range(n). L’algorithme de recherche est le suivant : on suppose correctement placées k dames dans les k premières colonnes. On cherche alors à placer une dame de plus dans la colonne suivante (d’indice k donc), en progressant suivant les indices croissants de lignes. Si k vaut n alors c’est qu’une position est trouvée.
On écrira une fonction récursive dames(cols, n) où cols est une liste des indices de lignes où on a déjà placé sans collision des dames et n est la taille de l’échiquier.
Plus précisément, soit un appel dames(cols, n) où cols est une liste de k entiers entre 0 et n-1 représentant des indices de lignes de l’échiquier. Alors, cet appel affichera toutes les solutions au problème telles que pour chaque indice de colonne \(\mathtt{j<k}\), la dame de cette colonne soit placée à la ligne d’indice cols[j]. Par exemple, l’appel dames([3, 0, 4, 7], 8) devra afficher :
[3, 0, 4, 7, 1, 6, 2, 5]
[3, 0, 4, 7, 5, 2, 6, 1]
le premier tableau représentant la solution montrée en début d’énoncé.
La recherche sera lancée par un appel dames([], n) et affichera chacune des solutions (ou les comptera).
On écrira une fonction de détection de collision. Plus précisément, on se donne deux colonnes \(\mathtt{col1}\) et \(\mathtt{col2}\) telle que \(\mathtt{col1 < col2}\). On suppose que
- \(\mathtt{col1}\) contient exactement une dame à la ligne d’indice
d1 - \(\mathtt{col2}\) contient exactement une dame à la ligne d’indice
d2
Un appel collision(col1, d1, col2, d2) renvoie True si les deux dames sont en prises et False sinon.
On écrira aussi une fonction is_valid(sol, i) qui, étant donnée
- une liste
soldekindices de lignes où sont placées des dames - une dame placée dans la colonne d’indice
ket à la lignei
renvoie True si la dame en colonne d’indice k n’est pas en prise et False sinon.
Pour n = 13, on devra trouver 73712 placements possibles.
En complément, et si vous n’êtes pas en séance de TP, vous pourrez consulter ce message du forum Python d’OpenClassrooms.
34. Le problème du cavalier d’Euler¶
On place un cavalier sur un échiquier et on cherche à faire parcourir par le cavalier toutes les cases de l’échiquier sans jamais passer deux fois sur la même case :
Ci-dessous, le cavalier commencera le parcours depuis la case dans le coin en haut à gauche. On numérotera les cases par un couple (i, j) indiquant la ligne et la colonne, i et j variant dans range(8).
Ecrire un fonction récursive cavalier(P, L) où P est le plateau marqué par les cases qui ont été occupées par le cavalier courant et L la liste courante des positions successives du chemin que le cavalier a emprunté avant d’arriver au dernier élément de la liste L. Le plateau est représenté par une liste de 8 listes, au départ remplies de huits zéros, sauf en position (0, 0) où la valeur sera 1. Quand le cavalier occupera une case, elle sera marquée 1 dans le plateau P. La fonction sera lancée par cavalier(P, L) où L = [(0,0)] et P initialisé comme indiqué ci-dessus.
L’algorithme consistera à
- considérer la dernière position
(i, j)occupée par le cavalier, à savoir la dernière valeur deL, - examiner les cases à portée du cavalier depuis la case
(i, j), - sélectionner les cases non déjà occupées (on les connaît grâce au plateau
P) - relancer le parcours depuis chacune de ces cases avec un appel récursif (sans oublier de mettre à jour
PetLavant l’appel). - replacer, après les appels récursifs, le plateau
Pet la listeLdans leur état antérieur (c’est le backtrack).
Par commodité, on pourra écrire une fonction voisin(i, j) qui renvoie la liste des cases à portée du cavalier placé en position (i, j).
On surveillera la longueur de la liste L et, une fois une solution trouvée, on interrompra la fonction cavalier en levant une exception du type StopIteration ou en appelant exit.sys(0) car un simple return ne suffirait pas. La recherche pourra durer plusieurs dizaines de secondes.
On pourra afficher le parcours effectué, par exemple :
1 60 39 34 31 18 9 64
38 35 32 61 10 63 30 17
59 2 37 40 33 28 19 8
36 49 42 27 62 11 16 29
43 58 3 50 41 24 7 20
48 51 46 55 26 21 12 15
57 44 53 4 23 14 25 6
52 47 56 45 54 5 22 13
35. Algorithme de remplissage¶
On donne un tableau de pixels blancs et noirs sous la forme d’une liste de listes, par exemple
L=[
['0', '0', '0', '1', '0', '0', '0'],
['0', '0', '0', '1', '0', '0', '0'],
['0', '0', '1', '0', '0', '0', '0'],
['1', '1', '0', '0', '0', '1', '1'],
['0', '0', '0', '0', '1', '0', '0'],
['0', '0', '0', '1', '0', '0', '0'],
['0', '0', '0', '1', '0', '0', '0']]
et affiché de manière plus lisible comme ci-dessous :
0 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 1 0 0 0 0
1 1 0 0 0 1 1
0 0 0 0 1 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 0
où, dans la liste, le blanc est codé par le caractère '0' et le noir par le caractère '1'.
On choisit un pixel du tableau L et on demande de colorer avec une 3e couleur toute la zone connexe constituée du pixel choisi et des pixels voisins et ayant la même couleur que le pixel choisi. La couleur de remplissage sera représentée par le caractère « X » et sera placé dans la liste L. Le pixel sera choisi par ses indices de ligne et colonne (commençant à 0).
Avec le tableau de pixels de l’exemple ci-dessus, et le pixel en position (3, 3) la liste deviendra :
L=[
['0', '0', '0', '1', 'X', 'X', 'X'],
['0', '0', '0', '1', 'X', 'X', 'X'],
['0', '0', '1', 'X', 'X', 'X', 'X'],
['1', '1', 'X', 'X', 'X', '1', '1'],
['X', 'X', 'X', 'X', '1', '0', '0'],
['X', 'X', 'X', '1', '0', '0', '0'],
['X', 'X', 'X', '1', '0', '0', '0']]
ou de manière plus lisible :
0 0 0 1 X X X
0 0 0 1 X X X
0 0 1 X X X X
1 1 X X X 1 1
X X X X 1 0 0
X X X 1 0 0 0
X X X 1 0 0 0
ou de façon animée :
On écrira une fonction récursive remplir(L, pos, coul) où pos est la position courante d’essai d’écriture et coul la couleur qu’il faut remplacer.
Pour plus d’information, on pourra consulter l’article Flood fill.
36. Suite de Syracuse en récursif¶
Soit la fonction \(\mathtt{f}\) définie pour \(\mathtt{n> 0}\) entier par :
\(\mathtt{f(n)}=\begin{cases}\mathtt{n/2}& \text{si } \mathtt{n} \text{ est pair}\\\mathtt{3n+1}& \text{sinon}\end{cases}\)
par exemple f(13) = 40 ou f(10) = 5.
Coder cette fonction. Tester avec \(\mathtt{f(13)}\) et \(\mathtt{f(10)}\).
On itère la fonction \(\mathtt{f}\) en partant d’un entier \(\mathtt{n}\). Par exemple, si \(\mathtt{n=13}\), on obtient :
13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1La conjecture de Syracuse affirme que si on itère \(\mathtt{f}\) depuis n’importe quel entier \(\mathtt{n>0}\) alors, on tombera forcément sur 1 ( comme c’est le cas dans l’exemple ci-dessus).
Écrire une fonction récursive
saut(x)qui renvoie le nombre d’itérations pour arriver à 1 quand la suite commence avec \(\mathtt{x}\) (par exemple, si \(\mathtt{x=13}\) alors il y a donc 9 itérations pour arriver à 1).Tester et vérifier en écrivant une version non récursive de la fonction
saut.
37. Algorithme d’Euclide en récursif¶
On rappelle que le pgcd de deux entiers désigne le plus grand diviseur commun à ces deux entiers. Par exemple pgcd(140, 100) = 20 : en effet, 140 et 100 sont des multiples de 20 et il n’existe aucun entier plus grand que 20 qui vérifie cette propriété.
L’algorithme d’Euclide permet de calculer de manière efficace le pgcd de deux entiers a et b. Si vous ne connaissez pas l’algorithme ou si vous ne l’avez plus bien en tête, regardez cette vidéo.
Voici quelques détails qui ne sont pas indispensables pour répondre à la question posée ci-dessous. L’algorithme est basé sur l’observation suivante : si b est non nul, le pgcd de a et de b est aussi le pgcd de b et du reste de la division entière de a par b. Par exemple, comme 140 % 100 = 40, on pgcd(140, 100) = pgcd(100, 40). On peut recommencer, ce qui donne pgcd(100, 40) = pgcd(40, 20) et continuer pgcd(40, 20) = pgcd(20, 0) ; cette fois on ne peut plus continuer puisque b = 0 (et on ne peut pas diviser par 0). Mais pgcd(a, 0) vaut toujours a et donc, ici, pgcd(140, 100) = 20. L’algorithme d’Euclide consiste donc à faire des divisions successives par le reste et à renvoyer le dernier reste non nul.
Ecrire une fonction récursive pgcd(a, b) qui retourne le plus grand diviseur commun de deux entiers a et b par l’algorithme d’Euclide. Tester et vérifier que votre fonction en comparant avec la fonction gcd du module math.
38. Fibonacci rapide¶
Soit \(F=0, 1, 1, 2, 3, 5, 8, \dots\) la suite de Fibonacci ; on notera \(F_n\) le terme d’indice \(n\geq 0\) de cette suite, par exemple, \(F_6=8\). On peut démontrer que la suite de Fibonacci vérifie les relations suivantes : \(F_0=0\), \(F_1=1\) et
\(\begin{cases} F_{2n}=F_n(2F_{n-1}+F_n)\\F_{2n+1}=F_n^2+F_{n+1}^2\end{cases}\)
Écrire un algorithme récursif qui calcule le \(n\)-eme terme de la suite de Fibonacci. Calculer \(F_n\) pour \(n\) valant 10 millions (compter de l’ordre de plusieurs dizaines de secondes, ça dépend de la puissance du processeur) et vérifier que les 10 premiers chiffres sont 1129834378 (envoyer le nombre dans un fichier pour pouvoir lire).
39. Coefficient binomial rapide¶
On a vu dans le cours que la fonction récursive basée sur la formule
\(\ds{n\choose p}={n-1\choose p-1}+{n-1\choose p-1}\)
est un calcul inefficace d’un coefficient binomial puisque le calcul d’un simple coefficient binomial tel que \(\ds{30\choose 15}\) peut nécessiter plusieurs minutes.
A partir de la formule
\(\ds{n\choose p}=\frac{n}{p}{n-1\choose p-1}\),
écrire une fonction binomial(n, p) qui calcule le coefficient binomial \(\ds{n \choose p}\) et vérifier que le calcul de binomial(30, 15) est alors instantané.
40. Coefficients binomiaux via le tableau de Pascal¶
On a vu dans le cours que la fonction récursive « évidente » basée sur la formule
\(\ds{n\choose p}={n-1\choose p-1}+{n-1\choose p-1}\)
ne permet pas, telle quelle, un calcul efficace d’un coefficient binomial. Toutefois, il est facile d’émuler récursivement la génération ligne par ligne du tableau de Pascal et obtenir ainsi un calcul efficace de chaque coefficient binomial.
Il est inutile de créer la totalité du tableau 2D, une ligne « extensible » suffit. En effet, si on dispose d’une liste comme L=[8, 4, 7, 2, 3] on peut construire la liste LL commençant par 1 suivi des sommes de termes voisins, dans notre cas LL=[1, 12, 11, 9, 5] et ce procédé permet de générer une ligne du tableau de Pascal connaissant la précédente.
Ecrire une fonction (non récursive)
next_line(L)qui partant d’une liste d’entiers, construit la listeLLcommençant par 1 et dont les termes suivants sont les sommes des paires de termes successifs deL, comme dans l’exemple ci-dessus.En déduire une fonction récursive
nth_line(n)qui renvoie la ligne d’indicendu tableau de PascalEn déduire une fonction non récursive
pascal(n, p)retournant le coefficient binomial aux indicesnetp.Bien sûr, cette fonction
pascalserait améliorable : ainsi,pascal(2000, 3)calcule la totalité de la ligne d’indice1999alors que seulement les 4 premiers termes sont nécessaires.
41. Maximum en récursif¶
Ecrire une fonction récursive maxi(L, p) qui calcule le plus grand des éléments d’indices \(\mathtt{i \geq p}\) d’une liste L non vide d’entiers et où \(\mathtt{p\geq 0}\) est censé être un indice valide de L. Appliquer au calcul du plus grand élément d’une liste.
42. Plus petit et plus grand élément (version récursive)¶
Soient une liste \(L\) d’entiers, de longueur \(n>0\) et \(k\) un entier tel que \(1\leq k\leq n\). Ecrire une fonction récursive min_max(L, k) qui renvoie la liste de deux éléments [m, M] constituée
- du plus petit élément
m - du plus grand élément
M
choisis parmi les \(k\) premiers éléments de la liste L.
Voici quelques exemples de comportements de la fonction :
L = [42, 81, 31, 81, 12, 99, 81], k = 4 --> [31, 81]
L = [42, 81, 31, 81, 12, 99, 81], k = 2 --> [42, 81]
L = [42], k = 1 --> [42, 42]
L = [42, 42, 42, 42], k = 3 --> [42, 42]
Explication du premier exemple. Comme \(k=4\), on recherche le plus petit et le plus grand élément des 4 premiers éléments de la liste L autrement dit, le plus petit et le plus grand élément de la liste [42, 81, 31, 81]. Le plus petit élément est bien 31 et le plus grand est bien 81 d’où la réponse [31, 81].
43. Somme récursive¶
Ecrire une fonction récursive \(\texttt{somme(L, p)}\) qui calcule la somme des \(\texttt{p}\) premiers éléments d’une liste \(\texttt{L}\) d’entiers. Utiliser cette fonction pour calculer la somme des éléments d’une liste.
44. Test de croissance¶
On donne une liste non vide L d’entiers et on demande d’écrire une fonction récursive estCroissante(L, i) qui renvoie True si à partir de l’indice i, la liste L est triée dans l’ordre croissant et False sinon. Utiliser cette fonction pour tester si une liste non vide L d’entiers est triée ou pas dans l’ordre croissant.
45. Alternance de signe dans une liste, version récursive¶
Écrire une fonction récursive \(\mathtt{f}\) qui prend en paramètre une liste \(\mathtt{L}\) d’entiers non nuls et un indice \(\mathtt{i}\) et qui renvoie True si les éléments de \(\mathtt{L}\) à partir de l’indice \(\mathtt{i}\) se suivent en alternant de signe (et False sinon). Par exemple, \(\mathtt{f([-5, 2, -4, 7], 1)}\) de même que \(\mathtt{f([3, -5, 2, -4, 7], 1)}\) ainsi que \(\mathtt{f([-2],0)}\) vaudront True tandis que \(\mathtt{f([-5, 2, 4, -7], 1)}\) ou encore \(\mathtt{f([5,-3,-1],0)}\) vaudront False. Pour tester si une liste complète \(\mathtt{L}\) est en alternance de parité, on lancera \(\mathtt{f(L, 0)}\).
46. Liste en alternance de zéro et un¶
Écrire une fonction récursive alterne(L) qui teste si une liste L est constituée de 0 et de 1 en alternance.
Exemples de comportement :
[0, 1, 0, 1] -> True
[1, 0, 1, 0] -> True
[1, 0, 1, 2, 0] -> False
[1] -> True
[0] -> True
[0, 0, 0, 0] -> False
[] -> True
[1, 1, 0, 0, 0] -> False
[1, 1, 1] -> False
On utilisera des slices.
47. Nombre d’inversions d’une liste¶
On donne une liste L d’entiers, par exemple
[5, 5, 4, 11, 9, 1, 5]
On appelle inversion de L tout couple (a, b) de valeurs dans L telles que :
aapparaisse à gauche deb- \(\mathtt{a > b}\).
Par exemple, (4, 1) est un inversion de la liste précédente.
Ecrire une fonction récursive nb_inversions(L) qui renvoie le nombre d’inversions de la liste L. Dans le cas de l’exemple ci-dessus, comme les inversions de L sont :
5 4
5 1
5 4
5 1
4 1
11 9
11 1
11 5
9 1
9 5
nb_inversions(L) doit renvoyer 10.
48. Eléments distincts d’une liste¶
On donne une liste L d’entiers et on veut écrire une fonction récursive distincts qui renvoie la liste M formée des éléments distincts de la liste L. Exemples :
[4, 3, 5, 4] -> [4, 3, 5]
[2, 5] -> [2, 5]
[1, 1, 3, 3, 2] -> [1, 3, 2]
[3, 1, 1, 1] -> [3, 1]
[1, 1] -> [1]
[5] -> [5]
[2, 1, 2, 1, 2] -> [2, 1]
On utilisera des slices.
49. Nombre d’occurrences dans une liste¶
On donne une liste L d’entiers et un entier a et on demande d’écrire une fonction récursive count(L, a) qui renvoie le nombre d’occurrences de a parmi les éléments de L. On utilisera des slices.
Exemples de comportements :
[31, 42, 81, 12, 42, 81, 42, 32, 42]
42 → 4
32 → 1
75 → 0
50. Ordre lexicographique¶
Étant donné deux listes L, M, l’une ou l’autre vide ou alors formées d’entiers, on peut comparer lexicographiquement L et M : c’est comme l’ordre dans un dictionnaire, les lettres étant remplacées par les entiers de chaque liste, voir les exemples ci-dessous. En Python, la comparaison L <= M utilise justement par défaut l’ordre lexicographique.
Ecrire une fonction récursive lexico(L, M) qui renvoie True si L <= M au sens lexicographique et False sinon. Evidemment, il ne faut pas utiliser d’opérateur de comparaison, tel que <=, entre listes.
Les exemple ci-dessous permettent de bien comprendre comment fonctionne l’ordre lexicographique :
L = [1, 2, 1, 2]
M = [2, 2, 2]
True
---------------
L = [3, 2, 1]
M = [1, 1]
False
---------------
L = []
M = [1, 3, 3]
True
---------------
L = [1, 3, 2]
M = []
False
---------------
L = [1, 3, 1, 2]
M = [1, 3]
False
---------------
L = [3]
M = [3, 1, 3]
True
---------------
L = [1]
M = [2]
True
51. Aplatir une liste¶
On définit les objets de type « liste-entier ». Avant de donner une définition, voici des exemples d’objets de type « liste-entier » :
[42, 81, 33][42, [81, [33, 21], 100], [33]][42, [81, [33, 21, []], 100], [[33], 10, [[]]]]
Plus généralement, on construit récursivement les objets suivants, dit de type « liste-entier » :
- la liste vide est de type « liste-entier »
- toute liste d’entiers est de type « liste-entier »
- si
Lest de type « liste-entier » alors, l’objet[[L]]est encore de type « liste-entier » - si
LetMsont de type « liste-entier » alors, l’objet[L, M]est encore de type « liste-entier »
Ecrire une fonction récursive aplatir(L), qui renvoie, sous forme de liste, les entiers d’une liste de type « liste-entier » (en anglais list flattening).
Voici quelques exemples de comportements :
[42, 81] -> [42, 81]
[] -> []
[[]] -> []
[[33, 17], [], [56, [15, 33, [21, 42]], 14], [22, 81]]
-> [33, 17, 56, 15, 33, 21, 42, 14, 22, 81]
[42, [], [17, [33, 52]], [[51, [], 55]], [[]]]
-> [42, 17, 33, 52, 51, 55]
52. Recherche dichotomique sans slices¶
Dans le cours, la recherche dichotomique a été présentée mais en utilisant la facilité des slices.
Reprendre le problème de la recherche dichotomique mais sans utiliser de slices. On écrira une fonction récursive dicho(L, x, i, j) qui renvoie True si l’objet x est présent dans la liste L à un indice entre i et j, ces indices étant inclus et qui renvoie False autrement. On écrira un appel qui teste la présence de x dans la liste L complète. On fera de nombreux tests, en particulier avec la liste utilisée dans le cours :
L = [12, 31, 46, 53, 81, 81, 82]
pour vous assurer que votre code est correct.
53. Générer une formule¶
On part de l’entier 1 et on s’autorise soit à ajouter 5 soit à multiplier par 3. Par exemple, on peut obtenir \(\mathtt{n=42}\) de la manière suivante :
a = 3 x 1 = 3
b = 3 x a = 9
c = 5 + b = 14
n = 3 x 14 = 42
en sorte qu’on a la formule suivante :
42 = 3 x (5 + 3 x 3)
Ecrire une fonction récursive formule(n) qui renvoie une formule comme ci-dessus s’évaluant à n et None si ce n’est pas possible. On essaiera d’éviter les parenthèses et les 1 inutiles.
En particulier, on pourra obtenir les formules suivantes :
2022 = 3 x (5 + 3 x (5 + 5 + 3 x (5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 1)))
2023 = 5 + 5 + 3 x (5 + 3 x (3 x (5 + 3 x (5 + 3 x (5 + 1)))))
2024 = 5 + 3 x (5 + 5 + 3 x (5 + 3 x (3 x (3 x (5 + 3)))))
2025 = impossible
2026 = 5 + 5 + 3 x (3 x (5 + 3 x (5 + 5 + 3 x (5 + 5 + 5 + 5 + 1))))
On utilisera la concaténation de chaînes :
a= "Py"
b= "Thon"
print(a + b)
qui affiche
PyThon
Cette question est proposée dans la 3e édition de Eloquent Javascript.
54. Somme de sous-ensembles nulle¶
On donne une liste de nombres entiers, par exemple
L=[-98, 35, 12, 7, 42, -2, -99, -87, -10, 42, -44]
Ecrire une fonction récursive qui renvoie une sous-liste de la liste formée d’éléments dont la somme est nulle et qui renvoie None si une telle sous-liste n’existe pas. Dans le cas de la liste ci-dessus, la fonction pourra renvoyer :
[12, 42, -10, -44]
Pour la liste
[62, -38, -45, -99, -68, -15, 62, -6, -85]
la fonction renverra None.
Dans la somme, chaque terme ne peut apparaître plus de fois qu’il n’est présent dans la liste initiale. La fonction devra pouvoir traiter des listes ayant jusqu’à 25 éléments.
Il s’agit du fameux problème dit Subset sum problem.
55. Plus longue sous-séquence croissante¶
On donne une liste d’entiers et on demande d’extraire de la liste une succession
- strictement croissante d’éléments,
- placés à des indices strictement croissant
- la plus longue possible.
Pour la suite ci-dessous,
0 8 4 12 2 10 6 14 1 9 5 13 3 11 7 15
une sous-suite strictement croissante de longueur maximale est 0 2 6 9 11 15.
On écrira une algorithme récursif « naïf » et qui devrait pouvoir traiter n’importe quelle liste de longueur 20 (mais beaucoup de listes aléatoires de taille 100). Votre code doit pouvoir passer les tests proposés au problème Easy Longest Increasing Subsequence sur le site SPOJ. Sur Leetcode, vous passerez 22 tests sur 54.
Il s’agit d’un problème classique.
56. Tirage du loto en récursif¶
Implémenter un tirage des 6 numéros du loto à l’aide d’une fonction récursive. Votre fonction aura la signature suivante
loto(interdits, n)
et elle renverra un tirage de \(\mathtt{n}\) numéros entre 1 et 49 et tels qu’aucun numéro ne soit dans la liste des interdits. Le tirage du loto sera lancé par loto([], 6).
57. Chiffres parmi 1 ou 8¶
Ecrire une fonction récursive chiffres81(n) qui renvoie la liste de tous les entiers positifs ayant \(\mathtt{n}\) chiffres et dont tous les chiffres sont parmi 1 ou 8. Par exemple, pour n=3, la fonction renvoie la liste suivante :
[111, 811, 181, 881, 118, 818, 188, 888]
On pourra utiliser que tout nombre à n chiffres s’écrit sous la forme \(\mathtt{n=10d+u}\) où \(\mathtt{d}\) est un nombre à \(\mathtt{n-1}\) chiffres et \(\mathtt{u}\) est le chiffre des unités ; par exemple, \(\mathtt{818 = 81\times 10+ 8}\).
58. Liste de zéros ou uns¶
Ecrire une fonction récursive in01(L) qui teste si la liste L est constituée d’éléments parmi 0 ou 1. Exemples de comportements :
[0, 1, 0] -> True
[[1, 1, 2] -> False
[0, 0] -> True
[0] -> True
[1, 0, 0, 2, 0] -> False
On utilisera des slices.
59. Chiffres à l’envers en récursif et sans liste¶
Ecrire une fonction inverser(n, m) qui prend en argument un entier positif n et renvoie l’entier dont l’écriture en base 10 est l’envers de l’écriture en base 10 de n. Par exemple, si n=2038 alors inverser renvoie 8302 et si n=2100 alors inverser renvoie 12. Le rôle de m est expliqué ci-dessous.
Contraintes : le programme ne doit utiliser aucune liste, ni les fonctions str ou int. La fonction inverser sera récursive et aura pour signature inverser(n, m) où m est un paramètre auxiliaire servant à conserver une valeur utile pour la récursion. Le schéma suivant pourra aider à comprendre comment bâtir inverser :
2038 0
203 8
20 83
2 830
0 8302
En déduire le code d’une fonction inverserChiffres(n) qui renvoie le nombre dont les chiffres sont les chiffres décimaux de n mais écrits à l’envers comme indiqué ci-dessus.
60. Produit des chiffres d’un entier¶
Observez d’abord cet exemple : prenons l’entier \(\mathtt{n=2024}\) et écrivons la division entière de \(\mathtt{n}\) par 10 sous la forme \(\mathtt{n = 2024= 10\times 202 + 4}\).
On remarque que cette écriture fait apparaître \(\mathtt{u=4}\) qui est le chiffre des unités de \(\mathtt{n}\) et \(\mathtt{d=202}\) qui est le nombre obtenu à partir de \(\mathtt{n}\) en supprimant le chiffre des unités. Plus généralement, tout nombre entier \(\mathtt{n\geq 0}\) s’écrit sous la forme \(\mathtt{n=10d+u}\) où \(\mathtt{d}\) est un entier positif et \(\mathtt{u}\) est un entier tel que \(\mathtt{0\leq u\leq 9}\). L’entier \(\mathtt{u}\) est juste le chiffre des unités de \(\mathtt{n}\) et \(\mathtt{d}\) est juste le nombre de dizaines de \(\mathtt{n}\). Il est essentiel pour la suite de l’exercice de voir que \(\mathtt{d}\) et \(\mathtt{u}\) s’obtiennent facilement en posant la division entière de \(\mathtt{n}\) par 10.
Ecrire une fonction récursive produit qui calcule le produit des chiffres d’un entier \(\mathtt{n}\). Par exemple, produit(547256) vaudra \(\mathtt{5\times 4\times 7\times 2\times 5\times 6=8400}\).
61. Produit palindromique¶
Cet exercice a été imaginé par mon collègue Thierry Montaut.
Ecrire une fonction récursive solve(n) qui détermine le plus petit entier \(\mathtt{k\geq n}\) qui multiplié par son écriture inversée (en base 10) est un palindrome. On utilisera des fonctions récursives sans aucune boucle.
Par exemple, si n=2018 alors k=2021 car \(\mathtt{2021 \times 1202 = 2429242}\) qui est un nombre palindrome sans que ce soit vrai pour k parmi 2018, 2019 ou 2020.
62. Nombre de décompositions en somme de puissances¶
On se donne un entier \(\mathtt{n\geq 1}\) et un exposant entier \(\mathtt{k\geq 2}\) et on cherche à déterminer le nombre de façons de décomposer \(\mathtt{n}\) en une somme de puissances \(\mathtt{k}\)-èmes distinctes et non nulles. Par exemple, si \(\mathtt{n=100}\) et \(\mathtt{k=2}\) alors la réponse attendue est 3 car il existe exactement 3 façons d’écrire 100 comme une somme de carrés distincts et non nuls, à savoir
\(100=10^2=6^2+8^2=1^2+3^2+4^2+5^2+7^2.\)
De même, si \(\mathtt{n=4}\) et \(\mathtt{k=2}\) alors la réponse attendue est 1 car la seule décomposition est \(\mathtt{4=2^2}\). La décomposition \(\mathtt{4=1^2+1^2+1^2+1^2}\) n’est pas valide car les puissances doivent être distinctes.
Ecrire une fonction récursive decomp(n, k) qui renvoie le nombre de décompositions de n en somme de puissances d’exposant \(\mathtt{k}\).
Cet exercice provient du site HackerRank.
63. Le tri fusion¶
Le tri fusion est un tri par comparaison récursif. Montrons sur un exemple comment il fonctionne. Soit la liste d’entiers :
T=[2, 11, 15, 16, 3, 4, 7, 17, 5, 4, 3, 16, 1]
Le tri fusion (fonction mergesort) coupe la liste en deux sous-listes L et R (pour left et right) de longueur aussi proches que possible (grosso modo la moitié de T) :
L=[2, 11, 15, 16, 3, 4]
R=[7, 17, 5, 4, 3, 16, 1]
puis, par deux appels récursifs, mergesort(L) et mergesort(R) trient la première puis la seconde sous-liste :
LL=[2, 3, 4, 11, 15, 16]
RR=[1, 3, 4, 5, 7, 16, 17]
Il ne reste plus qu’à fusionner les deux listes croissantes LL et RR pour obtenir le tri de la liste initiale :
TT=[1, 2, 3, 3, 4, 4, 5, 7, 11, 15, 16, 16, 17]
et il se trouve que l’opération de fusion de liste croissantes est simple et assez peu coûteuse à réaliser.
Le but de l’exercice est d’écrire un tri fusion, même s’il sera peu optimisé. On utilisera des slices.
- Soit la fonction
merge(L, R)qui partant de deux listes triées renvoie une nouvelle liste qui est la liste triée de la réunion des deux listes.- Ecrire une version récursive de
merge, sans aucune boucle. - Ecrire une version itérative de
merge.
- Ecrire une version récursive de
- En déduire une fonction
mergesort(T)qui implémente le tri fusion de la listeT. - Avec la version récursive de
merge, tester sur des listes aléatoires d’un peu moins de 1000 éléments. - Avec la version itérative de
merge, tester sur des listes aléatoires de plusieurs millions d’éléments. Comparer avec la fonctionsorted(s’attendre à un temps de 10 à 20 fois plus rapide desortedpar par rapport àmergesort).
- En déduire une fonction
64. Somme géométrique¶
On peut illustrer l’égalité suivante
\(1/2+1/4+1/8+1/16+\dots = 1\)
par le dessin ci-dessous :
Ecrire une fonction récursive carre(cote) qui génère sous Turtle la figure ci-dessus. Cette fonction se contentera de couper en deux le carré puis de couper une moitié en deux avant de se rappeler elle-même.
65. Carrés emboîtés récursivement¶
On demande d’écrire une fonction récursive \(\mathtt{carres}\) qui va afficher (bibliothèque graphique Turtle ou Matplotlib), \(\mathtt{n}\) carrés emboîtés :
Plus précisément, on demande d’écrire une fonction \(\mathtt{carres(x,y, cote, delta, n)}\) qui affiche \(\mathtt{n}\) carrés emboîtés, le premier côté valant \(\mathtt{cote}\), la position initiale du coin supérieur droit étant au point de coordonnées \(\mathtt{depart = (x, y)}\) et la distance séparant les côtés de deux carrés voisins étant de \(\mathtt{delta.}\)
Le dessin ci-dessus a été réalisé sous Matplotlib pour les données suivantes
n=20
x=y=0
cote=100
delta=2
66. Emboîtements de carrés de couleurs alternées¶
On demande de dessiner un motif tel que le suivant :
Le motif est une succession de carrés concentriques formés de disques de couleur alternativement orange et bleue. Le carré extérieur est de côté n et formé de disques bleus (sur le dessin, \(\mathtt{n=12}\)).
On écrira une fonction récursive carres(pos, n, r, color) où pos désigne la position du coin en haut à gauche, n le côté du carré, r le rayon de chaque disque et color la couleur du bord extérieur.
67. Triangles emboîtés¶
Construire un emboîtements de triangles comme dans la figure ci-dessous.
Le principe est simple : étant donné un triangle \(ABC\), on construit un autre triangle \(UVW\) tel que \(U\) soit sur le segment AB et tel que \(AU=AB/10\) et de même pour les autres côtés :
Il suffit ensuite de répéter cette construction avec le triangle \(UVW\).
On aura besoin de la transformation \(\mathtt{T(P, Q)}\) qui renvoie les coordonnées du point placé à 1/10 de PQ à partir de P :
def T(P, Q):
return (P[0]+(Q[0]-P[0])/10, P[1]+(Q[1]-P[1])/10)
Noter que l’ordre des points P puis Q a son importance.
On écrira une fonction récursive emboiter(A, B, C, n) qui dessine les n triangles formés du triangle \(\mathtt{ABC}\) et des triangles emboîtés dans ABC.
Dans le dessin ci-dessus, il y a 25 triangles. Pour des raisons esthétiques, on préférera un triangle équilatéral pour triangle initial.
68. L’escalier du diable¶
L’escalier du diable ou l’escalier de Cantor est la courbe définie récursivement de la manière suivante :
- on se donne un entier \(\mathtt{n\geq 1}\) et deux points \(A\) et \(B\) (voir dessin ci-dessous) ;
- on trace un « plateau » horizontal \(CD\), à mi-hauteur et mi-largeur entre \(A\) et \(B\), de longueur \(\ds\frac 13 AB\) ;
- on recommence ainsi \(n-1\) fois entre \(A\) et \(C\) puis entre \(B\) et \(D\) ;
- lorsque les \(n\) plateaux sont tracés, on joint extrémité \(C\) de chaque plateau au point \(A\) et l’extrémité \(D\) de chaque plateau au point \(B\).
Voici l’escalier du diable pour \(n=1\) :
puis pour \(n=2\) :
On demande d’écrire une fonction récursive diable(A, B, n) qui dessine l’escalier du diable d’extrémités \(A\) et \(B\) et ayant \(\mathtt{n}\) marches.
On utilisera la fonction auxiliaire plateau(A,B) qui renvoie la liste des points \(\mathtt{C}\) et \(\mathtt{D}\).
def plateau(A, B):
xA, yA=A
xB, yB=B
dx=xB-xA
dy=yB-yA
m=0.5*(yA+yB)
C=(xA+1/3*dx, m)
D=(xB-1/3*dx, m)
return C, D
69. Courbe de Bolzano-Lebesgue¶
La courbe de Bolzano-Lebesgue est une courbe continue mais nulle part dérivable. La terminologie de « courbe de Bolzano-Lebesgue » figure sur cette page du site Math Curve.
On part d’un segment \(AB\) que l’on voit comme la diagonale d’un rectangle \(ACBD\). On construit le point \(M\) de coordonnées \((\frac 13, \frac 23)\) dans le repère \((A, AC, AD)\) et le point \(N\) de coordonnées \((\frac 23, \frac 13)\). On obtient la ligne brisée \(AMNB\), cf. dessin ci-dessous, la partie en noir. Et on recommence la construction avec les segments \(AM\), \(MN\), \(NB\).
Voici les courbes après une (en noir), deux (en bleu) et trois (en orange) répétitions :
Voici la courbe obtenue après 7 répétitions :
La diagonale de départ est d’extrémités \((-u, u)\) et \((u,u)\) avec \(u=350\).
On pourra utiliser la fonction auxiliaire suivante qui renvoie \(M\) et \(N\) ci-dessus à partir de \(A\) et de \(B\) :
def tiers(A,B):
xA, yA=A
xB, yB=B
dx=xB-xA
dy=yB-yA
xM=xA+1/3*dx
xN=xA+2/3*dx
yM=yA+2/3*dy
yN=yA+1/3*dy
return (xM,yM), (xN, yN)
70. Triangle de Sierpinski¶
La figure ci-dessous montre un triangle de Sierpinski de profondeur 3 :
On va détailler le principe de construction d’un triangle de Sierpinski de profondeur n. On part d’un triangle, de préférence équilatéral (trois côtés de même longueur) rempli en noir. La construction de base est la suivante :
- on calcule les milieux de chaque côté ce qui détermine 4 triangles ;
- on remplit en blanc le triangle central.
On obtient alors un triangle de Sierpinski de profondeur 1.
Cette opération est alors répétée sur chacun des 3 triangles noirs (c’est ici que la récursivité intervient). On obtient ainsi un triangle de Sierpinski de profondeur 2. Et ainsi de suite.
L’exercice consiste à coder une fonction récursive ts(T, n), de construction sous Matplotlib d’un triangle de Sierpinski T de profondeur n et de frontières les côtés délimités par les sommets de T.
Le remplissage initial ci-dessous :
a été obtenu par le code suivant :
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon
# Choisir la taille voulue
plt.gcf().set_size_inches(10,5)
def polygon(L, **kwargs):
my_polygon = Polygon(L, **kwargs)
plt.gca().add_patch(my_polygon)
# --------- Code du dessin --------------------------
a=(0,0)
b=(1,0)
c=(0.5, 3**.5/2)
T=[a, b, c]
polygon(T, fill=True, color="black")
# -------- FIN du code du dessin --------------------
plt.axis('equal')
plt.axis('off')
plt.show()
Ce triangle est un triangle de Sierpinki de profondeur 0.
On pourra utiliser la fonction suivante qui calcule les coordonnées du milieu d’un segment :
def milieu(u, v):
return ((u[0]+v[0])/2, (u[1]+v[1])/2 )
71. Cercles en arbre binaire¶
On demande de construire un motif formé de cercles tangents extérieurement et qui se contruit par générations : on adjoint à chaque cercle \(C\) créé à la génération courante, deux cercles de rayon moitié moins grand et tangents au cercle \(C\) au point situé au sud et au point situé à l’est. Par exemple, les motifs obtenus aux générations \(n=3\) et \(n=4\) sont les suivants :
La génération initiale est constitué d’un seul cercle. On écrira une fonction récursive, n’utilisant aucune boucle for et qui ne renvoie rien. On essayera de faire en sorte que chaque cercle soit dessiné une fois et une seule.
72. Courbe de Koch¶
On se propose de dessiner la courbe \(\mathtt{K}\) suivante :
avec la fonction récursive \(\texttt{koch(A, B, n)}\) où \(\texttt{A}\) désigne le point extrémité gauche de la courbe courante, \(\texttt{B}\) désigne le point d’extrémité droite de la courbe courante et \(\texttt{n}\) l’itération (sur le dessin, \(\mathtt{n=6}\)).
Décrivons d’abord l’action élémentaire (cf. figure ci-dessous).
On dispose des extrémités \(\mathtt{A}\) et \(\mathtt{B}\) d’un segment. On trace une ligne avec le procédé suivant :
- on coupe le segment AB aux tiers, on obtient les points C et D,
- on élève au milieu de CD le point M tel que le triangle CDM soit un triangle équilatéral direct,
- on trace la ligne ACMDB.
Ecrire une fonction récursive \(\texttt{koch(A, B, n)}\) qui partant d’un segment d’extrémités A et B (connus par leurs coordonnées sous forme de listes de deux entiers) dessine la ligne brisée ci-dessus après la \(\mathtt{n}\)-ème itération. On utilisera la fonction \(\texttt{equi(A,B)}\) donnée dans le code \(\texttt{equi.py}\) et qui renvoie la liste des trois sommets C, M et D (dans cet ordre, par leurs coordonnées) du triangle équilatéral.
On remarquera que la courbe à l’étape \(n>0\) s’obtient en juxtaposant convenablement 4 exemplaires de la courbe de l’étape \(n-1\). Si \(n=0\), la fonction tracera juste le segment entre \(\mathtt{A}\) et \(\mathtt{B}\).
Ci-dessous, la courbe obtenue pour \(\mathtt{n=2}\) puis \(\mathtt{n=3}\):
Voici le code de equi.py (qu’on se contentera d’utiliser) :
equi.py
from math import sqrt
def equi(A,B):
a,b=A
c,d=B
C=(2/3*a + 1/3*c, 2/3*b + 1/3*d)
M=(1/6*sqrt(3)*b - 1/6*sqrt(3)*d + 1/2*a + 1/2*c,
-1/6*sqrt(3)*a + 1/6*sqrt(3)*c + 1/2*b + 1/2*d)
D=(1/3*a + 2/3*c, 1/3*b + 2/3*d)
return C,M,D
73. La courbe de Hilbert¶
La courbe de Hilbert désigne une suite de lignes polygonales contenues dans un carré. Voici les 4 premières courbes :
Plus précisément, pour tout carré \(ABCD\) et pour chaque entier \(n\geq 1\), la courbe de Hilbert \(H_n\) relative au carré \(ABCD\) est une ligne polygonale définie récursivement de la manière suivante :
on découpe le carré \(ABCD\) en quatre sous-carrés de même dimension, numérotés 1, 2, 3 et 4 dans le sens direct (le sens inverse des aiguilles d’une montre) en commençant par le carré en haut à gauche ;
dans les deux carrés du bas (2 et 3), on construit les deux courbes de Hilbert \(H_{n-1}\) relatives à chacun des carrés ;
dans le carré 1 (en haut à gauche), on construit la courbe de Hilbert \(H_{n-1}\) mais après l’avoir tournée d’un quart de tour dans le sens direct ;
dans le carré 4 (en haut à droite), on construit la courbe de Hilbert \(H_{n-1}\) mais après l’avoir tournée d’un quart de tour dans le sens indirect ;
on relie les extrémités des courbes de Hilbert obtenues entre
- le carré 1 et le carré 2
- le carré 2 et le carré 3
- le carré 3 et le carré 4
La carré ne fait pas partie de la courbe. On conviendra que \(H_0\) est le centre du carré. Ecrire une fonction récursive hilbert(a, b, c , d, n) qui dessine la courbe de Hilbert \(H_n\) et où \(a\), \(b\), \(c\) et \(d\) sont les sommets du carrés énumérés dans le sens direct en commençant par le sommet en haut à gauche. Il pourra être utile que le retour de hilbert(a, b, c , d, n) soit la liste [u, v] des deux extrémités de la ligne polygonale.
Il pourra être utile d’utiliser la fonction milieu suivante qui renvoie la liste des coordonnées du milieu du segment d’extrémités a et b :
def milieu(a, b):
xa, ya=a
xb, yb=b
return [(xa+xb)/2, (ya+yb)/2]
74. Suite de Prouhet en récursif¶
La suite de Prouhet est la suivante :
0
01
0110
01101001
etc
Cette suite est une suite de chaînes composées de 0 et de 1 de la manière suivante : chaque chaîne T s’obtient à partir de la précédente U en adjoignant à U la suite V obtenue à partir de U en échangeant tout 0 en 1 et tout 1 en 0.
Ecrire une fonction récursive prouhet(n) qui renvoie la \(n\)-ème suite de Prouhet.
75. Tri par insertion récursif¶
On veut trier dans l’ordre croissant une liste L d’entiers de la manière suivante : si L contient au moins \(\mathtt{k\geq 2}\) entiers, on trie la liste LL formée des \(\mathtt{k-1}\) derniers éléments ; on appelle \(\mathtt{a}\) le premier élément de L et \(\mathtt{b}\) le premier élément de la liste triée LL ; si \(\mathtt{a>b}\) alors on échange les éléments \(\mathtt{a}\) et \(\mathtt{b}\) dans la liste L et on trie à nouveau la liste formée des \(\mathtt{k-1}\) derniers éléments ; ainsi, la liste L sera bien triée.
Implémenter l’algorithme précédent en utilisant une fonction récursive tri(L, d) où L est est une liste d’entiers et où la fonction trie tous les entiers de L à partir de l’indice d. Pour obtenir un tri de la liste L, on lancera donc tri(L, 0).
Tester le tri pour une liste aléatoire de quelques centaines d’entiers. On utilisera le code ci-dessous :
from random import randrange
def tri(L, d):
# Votre code
N=600
L=[randrange(N) for _ in range(N)]
tri(L, 0)
Vous observerez que le code est relativement lent (en fait, de complexité exponentielle). Essayez d’améliorer la fonction ci-dessus. En effet, lorsqu’elle procède au 2e tri, la liste, à partir de son deuxième élément, va être re-triée inutilement. Pour parer à cela, changez légèrement la signature de la fonction en
def tri(L, d, dejaTriee)
où dejaTriee est un « drapeau » valant True ou False et qui indique si la liste L est oui ou non déjà triée à partir de son 2ème élément. Re-testez la fonction et observez une nette amélioration des performances (bien que le tri reste un tri quadratique, dit lent).
76. Génération de toutes les parties d’un ensemble¶
Dans cet exercice, les ensembles sont codés sous forme de liste. Par exemple, l’ensemble \(\mathtt{A}\) formé des 4 éléments 81, 12, 31 et 65 sera codé sous la forme A = [81, 12, 31, 65]. L’ensemble ne contenant aucun élément sera noté [].
Soit un ensemble \(\mathtt{A}\), de taille \(\mathtt{n}\). Programmer en Python la génération de toutes les parties de \(\mathtt{A}\) autrement dit, écrire une fonction récursive powerset(A) qui renvoie la liste de toutes les parties de \(\mathtt{A}\) en sorte que cette fonction renvoie une liste de listes. On rappelle qu’un ensemble ayant \(\mathtt{n}\) éléments est formé de \(\mathtt{2^n}\) parties. Ainsi, powerset([81, 12, 31]) est une liste formée des 8 listes ci-dessous :
[]
[81]
[12]
[81, 12]
[31]
[81, 31]
[12, 31]
[81, 12, 31]
On notera que dans cette liste, figurent la partie vide (1e ligne) et l’ensemble lui-même (dernière ligne).
La méthode pour construire powerset(A) consiste à observer que si \(\mathtt{A}\) est une partie contenant un élément donné \(\mathtt{a}\) et si on note \(\mathtt{B}\) l’ensemble des éléments de \(\mathtt{A}\) autres que \(\mathtt{a}\) alors, toute partie de \(\mathtt{A}\) est
- soit une partie de \(B\),
- soit une partie de \(B\) complétée de la partie (« le singleton ») contenant uniquement \(\mathtt{a}\).
On précise qu’on peut concaténer deux listes L et M par l’opération L + M, par exemple :
L = [81, 12]
M = [31]
S = L + M
print(S)
[81, 12, 31]
77. Générer toutes les permutations récursivement¶
Une permutation d’un ensemble \(\mathtt{A}\) correspond juste à un suite contenant chaque élément de \(\mathtt{A}\) une fois et une seule. Par exemple, si \(\mathtt{A}\) est l’ensemble \(\mathtt{\{81, 12, 31, 65\}}\) alors la suite \(\mathtt{[81, 12, 31, 65]}\) est une permutation de \(\mathtt{A}\) mais \(\mathtt{[12, 31, 65, 81]}\) en est une autre, de même que \(\mathtt{[12, 31, 81, 65]}\).
Ecrire une fonction récursive perm(A) qui génère toutes les permutations d’un ensemble \(\mathtt{A}\) formé de \(\mathtt{n}\) éléments. L’ensemble \(\mathtt{A}\) sera implémenté via une liste de \(\mathtt{n}\) éléments. Toute permutation sera implémentée comme une liste d’éléments de \(\mathtt{A}\). Une permutation \(\mathtt{p}\) étant donnée, raisonner en fonction de l’élément en dernière position dans \(\mathtt{p}\).
On pourra utiliser que si on dispose de deux listes L et M alors L + M est une nouvelle liste formée des éléments de L suivis des éléments de M.
78. Générer toutes les parties ayant un nombre d’éléments donné¶
Générer toutes les parties à \(\mathtt{p}\) éléments d’un ensemble \(\mathtt{A}\) donné de \(\mathtt{n}\) éléments. Pour cela, on implémentera l’algorithme récursif naïf suivant : on se donne \(\mathtt{x}\) dans \(\mathtt{A}\) et on observe qu’une partie \(\mathtt{B}\) de \(\mathtt{A}\) ayant \(\mathtt{p}\) élément est obtenue :
- soit à partir de \(\mathtt{x}\) et d’une partie à \(\mathtt{p-1}\) élements ne contenant pas \(\mathtt{x}\)
- soit d’une partie à \(\mathtt{p}\) élements ne contenant pas \(\mathtt{x}\).
Quelle est l’énorme limitation de cette méthode ?
79. Partition en parties ayant 2 ou 3 éléments¶
On considère l’ensemble de tous les entiers entre \(\mathtt{1}\) et \(\mathtt{n}\) et on demande d’écrire une fonction récursive qui génère toutes les partitions de cet ensemble en parties ayant 2 ou 3 éléments. Par exemple, si n=6, on trouve 25 partitions parmi lesquelles figurent :
{1, 4}, {3, 5}, {2, 6}
{2, 4}, {3, 6}, {1, 5}
{2, 3, 5}, {1, 4, 6}
{4, 6}, {1, 3}, {2, 5}
Le nombre de telles partitions est répertorié sur le site OEIS. Le code devrait pouvoir générer en quelques dizaines de secondes les 4689685 de partitions correspondant à \(\mathtt{n=14}\).
Une partition pourra être vue comme une liste de listes de 2 ou 3 éléments. On s’assurera que l’on génère des partitions différentes. On pourra n’utiliser que des listes. Les slices et la fonction standard deepcopy pourront être utilisés.
Pour écrire la fonction récursive, on pourra isoler un élément \(\mathtt{a}\) de l’ensemble \(\mathtt{E}\) à traiter puis :
- générer les partitions dont un des éléments est la paire \(\mathtt{\{a, i\}}\) où \(\mathtt{i}\) varie en étant distinct de \(\mathtt{a}\) ;
- générer les partitions de \(\mathtt{E}\) privé de \(\mathtt{a}\) ;
- rajouter \(\mathtt{a}\) à chaque paire des partitions précédentes.
Cette question est apparue sur le forum Python du site OpenClassrooms.
80. Répartir \(n\) individus suivant \(k\) groupes¶
On cherche à répartir n individus discernables suivant \(\mathtt{k}\) groupes distincts.
Par exemple, s’il y a \(\mathtt{n=5}\) individus A, B, C, D et E et \(\mathtt{k=3}\) groupes, alors il y a exactement 150 répartitions possibles, comme :
- BE, AC, D
- E, A, BCD
- etc
Ecrire une fonction récursive groupes(n, k) qui renvoie la liste des regroupements. Les individus seront numérotés de 0 à \(\mathtt{n-1}\), et les groupes seront numérotés de 0 à \(\mathtt{k-1}\). Un regroupement sera vu comme une liste L de n entiers dans range(k), l’individu référencé par l’indice i appartenant au groupe L[i].
On pourra raisonner comme suit. Un groupe s’obtient
- soit en sélectionnant un groupe de \(\mathtt{n-1}\) individus répartis suivant \(\mathtt{k}\) groupes, le dernier individu étant placé dans un des
kgroupes ; - soit en sélectionnant un groupe de \(\mathtt{n-1}\) individus répartis suivant \(\mathtt{k-1}\) groupes, le dernier individu étant placé dans le groupe manquant.
Mathématiquement parlant, il s’agit de trouver toutes les surjections d’un ensemble à \(n\) éléments sur un ensemble à \(k\) éléments. Le nombre de telles surjections est \(k!\left\{\begin{matrix}n\\k\end{matrix}\right\}\) où \(\left\{\begin{matrix}n\\k\end{matrix}\right\}\) est un nombre de Stirling de seconde espèce.
81. Scores d’une partie de football¶
Si vous préférez le handball au football, l’exercice marche aussi !
Si le score final d’une partie de football est, par exemple 2-3, il y a 10 façons possibles pour le score d’avoir évolué du score initial de 0-0 vers le score final de 2-3 et dont la liste est donnée ci-dessous :
0-0, 1-0, 2-0, 2-1, 2-2, 2-3
0-0, 1-0, 1-1, 2-1, 2-2, 2-3
0-0, 0-1, 1-1, 2-1, 2-2, 2-3
0-0, 1-0, 1-1, 1-2, 2-2, 2-3
0-0, 0-1, 1-1, 1-2, 2-2, 2-3
0-0, 0-1, 0-2, 1-2, 2-2, 2-3
0-0, 1-0, 1-1, 1-2, 1-3, 2-3
0-0, 0-1, 1-1, 1-2, 1-3, 2-3
0-0, 0-1, 0-2, 1-2, 1-3, 2-3
0-0, 0-1, 0-2, 0-3, 1-3, 2-3
Plus généralement, écrire une fonction récursive score(p, q) qui renvoie la liste tous les scores possibles d’une partie de football qui se termine avec un score de p buts pour la première équipe et q buts pour la 2e équipe.
82. Changer des prénoms par d’autres¶
On dispose d’un texte tel que
Si Pierre est le fils de Paul, et si Paul est le frère de Jacqueline, qui est Pierre pour Jacqueline ?
et on souhaite effectuer des substitutions de prénoms, pour que la nouvelle phrase soit
Si Paul est le fils de Tom, et si Tom est le frère de Mathilde, qui est Paul pour Mathilde ?
en sorte qu’on fait les substitutions suivantes :
- Pierre → Paul
- Paul → Tom
- Jacqueline → Mathilde
Ecrire une fonction récursive subs(text, names, alt) qui effectue dans text la substitution des noms de names par les noms de alt. On pourra procéder comme suit, en utilisant les méthodes de chaînes split et join :
- on découpe le texte (avec
split) par le premier prénom, - récursivement, on substitue dans les différents morceaux les autres prénoms,
- on recolle avec le prénom alternatif au premier en utilisant
join.
Cet exercice trouve son origine dans une discussion sur le forum Python d’OpenClassrooms
83. Anagrammes¶
Ecrire une fonction récursive anagrammes(mot) qui génère tous les anagrammes d’un mot donné. On pourra raisonner de la manière suivante :
- considérer la première lettre possible de l’anagramme (c’est une parmi l’ensemble des lettres deux à deux distinctes du mot), disons
init; - la suite de l’anagramme est formée d’un anagramme bâti sur le mot ayant les mêmes lettres que le mot initial sauf que la lettre
initest privé d’une occurrence.
On utilisera des ensembles et des slices.
84. Obtenir une somme à partir de termes donnés¶
Cet exercice est inspiré du problème Composition de crêpes donné en demi-finale de Prologin 2018.
On donne une liste L d’entiers strictement positifs et une valeur entière s > 0 et on demande d’écrire une fonction récursive estSomme(L, s) qui renvoie True si on peut obtenir s comme somme d’éléments de L et placés à des indices distincts.
Par exemple, si L=[8, 2, 1, 3] et
- si
s=7alorsestSomme(L, s)renvoieFalse - si
s=11alorsestSomme(L, s)renvoieTrue.
Le code devrait pouvoir traiter en quelques secondes au plus une liste L aléatoire ayant jusqu’à 25 entiers.
85. Gain maximal aux dames¶
On donne le damier 10 x 10 d’une partie de dames en cours de déroulement :
Les pions noirs sont représentés par une croix (x) et les pions blancs par un cercle (o). Le damier est donné sous forme de chaîne de caractères, par exemple la chaîne triple :
damier = """\
.x........
..o.....o.
.x.....x..
..o.o.o...
...x......
..o.o..x..
.o...o....
..o.o.o...
...o......
....x....."""
C’est aux noirs de jouer.
On demande de calculer le nombre maximal de pions blancs qu’un pion noir peut « manger » (le pion est un pion simple, pas une « dame »). Pour cela on écrira une fonction récursive
manger(lig, col, damier)qui renverra le nombre maximal en question. Par exemple, dans la partie ci-dessus, ce nombre est 6. L’idée est simple :- on se donne un pion noir
- on regarde les sauts qu’il peut faire
- on lance récursivement la fonction pour chacun des sauts
- on prend le maximum des valeurs retournée
- on fait attention à remettre le plateau en état quand on termine la fonction récursive
- on refait la même pourchaque pion noir.
Modifier la fonction précédente pour qu’elle donne une succession maximale de prises. Par exemple, dans l’exemple ci-dessus, et si on numérote à partir de 0 le coin en haut à gauche, et qu’une position est donnée par un couple
(ligne, colonne), un chemin qui donne 6 prises est :[((2, 7), (4, 5)), ((4, 5), (2, 3)), ((2, 3), (4, 1)), ((4, 1), (6, 3)), ((6, 3), (8, 5)), ((8, 5), (6, 7))]
La question a été posée sur le forum Python d’OpenClassrooms.
86. Liste des partages¶
On appelle partage de l’entier \(s\geq 0\) toute liste croissante (au sens large) d’entiers strictement positifs et dont la somme vaut \(s\). Par exemple, les partages de \(6\) sont les 11 listes suivantes :
1 1 1 1 1 1
1 1 1 1 2
1 1 1 3
1 1 2 2
1 1 4
1 2 3
1 5
2 2 2
2 4
3 3
6
Pour la suite de l’exercice, il est important de garder en tête qu’un partage est une liste. Par exemple, la liste suivante [3, 6, 9, 11, 13] est un partage de 42. Et donc si on cherche la liste de tous les partages de s, on obtiendra une liste de listes d’entiers.
Ecrire une fonction récursive partage(k, s) qui renvoie la liste de tous les partages de l’entiers s et dont le premier terme est supérieur ou égal à k. Par exemple, partage(4, 17) doit renvoyer une liste de 12 listes et qui sont représentées ci-dessous :
4 4 4 5
4 4 9
4 5 8
4 6 7
4 13
5 5 7
5 6 6
5 12
6 11
7 10
8 9
17
Afficher tous les partages de 13. Vérifier qu’il y a 53174 partages de 42.
On pourra utiliser la méthode extend d’une liste qui permet d’étendre une liste par les éléments d’une autre liste comme le montre l’exemple ci-dessous :
L = [42, 31, 12, 81]
M = [10, 100, 1000]
print(L)
print(M)
print("----------")
L.extend(M)
print(L)
et qui affiche
[42, 31, 12, 81]
[10, 100, 1000]
----------
[42, 31, 12, 81, 10, 100, 1000]
87. Combinaisons via l’ordre lexicographique¶
On donne un entier \(\mathtt{n\geq 1}\) et soit \(\mathtt{p}\) un entier de
range(n)(pour l’exemple, je prendrain=5etp=3). On appellera mot une liste strictement croissanteLdepentiers derange(n), par exempleL=[1, 2, 4]. On cherche le mot qui suit immédiatementLdans l’ordre lexicographique. Par exemple, sin=5etL=[0, 2, 4]alors le suivant est[0, 3, 4]et le suivant encore est[1, 2, 3]dont le suivant est[1, 2, 4].Ecrire une fonction récursive
suivant(L,n)qui renvoie le mot qui suit immédiatementLdans l’ordre lexicographique. Ainsi,suivant([0, 2, 4], 5) = [0, 3, 4].En déduire une fonction
comb(n, p)qui liste toutes les combinaisons denobjets prispàp, une combinaison étant vue comme un mot au sens de la question 1.Appliquer à trouver tous les groupes de
ppersonnes que l’on peut constituer parminpersonnes. Par exemple, si on dispose de la liste de personnesP=["Amélie", "Benoît", "Clément", "Damien", "Énola", "Fanny", "Gauthier"]
les groupes de 3 personnes que l’on peut constituer sont :
['Amélie', 'Benoît', 'Clément'] ['Amélie', 'Benoît', 'Damien'] ['Amélie', 'Benoît', 'Énola'] ['Amélie', 'Benoît', 'Fanny'] ['Amélie', 'Clément', 'Damien'] ['Amélie', 'Clément', 'Énola'] ['Amélie', 'Clément', 'Fanny'] ['Amélie', 'Damien', 'Énola'] ['Amélie', 'Damien', 'Fanny'] ['Amélie', 'Énola', 'Fanny'] ['Benoît', 'Clément', 'Damien'] ['Benoît', 'Clément', 'Énola'] ['Benoît', 'Clément', 'Fanny'] ['Benoît', 'Damien', 'Énola'] ['Benoît', 'Damien', 'Fanny'] ['Benoît', 'Énola', 'Fanny'] ['Clément', 'Damien', 'Énola'] ['Clément', 'Damien', 'Fanny'] ['Clément', 'Énola', 'Fanny'] ['Damien', 'Énola', 'Fanny']
88. Paniers de fruits¶
Soit, par exemple, à dénombrer le nombre de paniers que l’on peut constituer avec 5 fruits choisis parmi des mangues, des oranges et des papayes. Un petit décompte montre qu’il existe 21 paniers possibles dont voici les compositions :
1 : 5 mangues,
2 : 4 mangues, 1 orange,
3 : 3 mangues, 2 oranges,
4 : 2 mangues, 3 oranges,
5 : 1 mangue, 4 oranges,
6 : 5 oranges,
7 : 4 mangues, 1 papaye
8 : 3 mangues, 1 orange, 1 papaye
9 : 2 mangues, 2 oranges, 1 papaye
10 : 1 mangue, 3 oranges, 1 papaye
11 : 4 oranges, 1 papaye
12 : 3 mangues, 2 papayes
13 : 2 mangues, 1 orange, 2 papayes
14 : 1 mangue, 2 oranges, 2 papayes
15 : 3 oranges, 2 papayes
16 : 2 mangues, 3 papayes
17 : 1 mangue, 1 orange, 3 papayes
18 : 2 oranges, 3 papayes
19 : 1 mangue, 4 papayes
20 : 1 orange, 4 papayes
21 : 5 papayes
Plus généralement, on veut déterminer le nombre de paniers composés d’un total de \(n\) fruits qui sont choisis parmi \(k\) variétés données. Dans l’exemple ci-dessus, \(n=5\) et \(k=3\).
Ecrire une fonction récursive
nb_paniers(k, n)qui renvoie le nombre de paniers possibles. Par exemple,nb_paniers(3, 5)doit renvoyer 21. On pourra raisonner en fonction du nombre de fruits dans la \(k\)-ème variété.On s’intéresse maintenant à la constitution des paniers. Ecrire une fonction récursive
composition_paniers(k, n)qui renvoie la liste des paniers. Un panier est une liste dekéléments, l’élément à l’indiceivalant le nombre de fruits du panier qui sont de la variété indexéei. Par exemple,composition_paniers(3, 5)doit renvoyer la liste des 21 listes suivantes :[5, 0, 0] [4, 1, 0] [3, 2, 0] [2, 3, 0] [1, 4, 0] [0, 5, 0] [4, 0, 1] [3, 1, 1] [2, 2, 1] [1, 3, 1] [0, 4, 1] [3, 0, 2] [2, 1, 2] [1, 2, 2] [0, 3, 2] [2, 0, 3] [1, 1, 3] [0, 2, 3] [1, 0, 4] [0, 1, 4] [0, 0, 5]
89. Régler avec un minimum de pièces de monnaie¶
On cherche à régler un montant avec des pièces choisies parmi des pièces de
- 2 unités
- 5 unités
- 9 unités
et on souhaite que le nombre de pièces utilisées pour régler soit minimum.
Par exemple, pour régler 25U, on peut n’utiliser que 4 pièces : \(\mathtt{25U = 1 \times 2U + 1 \times 5U + 2 \times 9U}\).
- Ecrire une fonction récursive
regler(m)qui renvoie une manière de régler(n2, n5, n9)le montantmavec un minimum de pièces ou qui renvoieNonesi le montant ne peut être réglé. On raisonnera suivant qu’on utilise soit une pièce de 2U, soit une pièce de 5U, soit une pièce de 9U. Vérifier queregler(62)=(1, 3, 5). - Associer à la fonction
regler(m)un procédé de mémoïzation comme vu dans le codage du tableau de Pascal pour traiter des valeurs bien plus grandes (de l’ordre de 1000). Vérifier queregler(993)=(1, 2, 109).
90. Nombre de rangements « confortables »¶
Observez d’abord cet exemple : soit une suite de \(\mathtt{7}\) cases vides, notée comme ceci
[0, 0, 0, 0, 0, 0, 0]
On veut déterminer le nombre de façons différentes de ranger \(\mathtt{3}\) boules dans les cases en sorte que deux boules ne soient jamais dans des cases côte-à-côte ; un tel rangement sera dit confortable. Une boule étant représentée par un 1, le rangement
[0, 1, 0, 1, 0, 1, 0]
ou encore le rangement
[1, 0, 0, 0, 1, 0, 1]
sont donc confortables ; en revanche, le rangement
[1, 0, 0, 1, 1, 0, 0]
ne l’est pas car la 4ème et la 5ème cases sont des cases voisines et occupées par des boules.
Plus généralement, on cherche à déterminer le nombre de rangements confortables de \(\mathtt{k}\) boules dans une succession de \(\mathtt{n}\) cases vides, autrement dit, les rangements où deux boules ne sont jamais placées dans des cases immédiatement voisines.
Résoudre ce problème en définissant une fonction récursive f(n, k) qui renvoie le nombre de rangements confortables. On raisonnera en considérant deux cas :
- ou bien la dernière case est vide et il suffit de placer les \(\mathtt{k}\) boules dans les \(\mathtt{n-1}\) premiers emplacements
- ou bien la dernière case est occupée par une boule et alors, il suffit de placer les \(\mathtt{k-1}\) autres boules dans les \(\mathtt{n-2}\) premiers emplacements.
Vous penserez à traiter au début du code de votre fonction récursive tous les cas d’exclusion du raisonnement ci-dessus.
Votre code doit pouvoir calculer en quelques secondes \(\mathtt{f(n, k)}\) pour un entier \(\mathtt{n\leq 35}\). Voici quelques exemples d’appels de la fonction f :
- f(4, 3) vaut 0 (il n’y a aucun rangement valide possible) ;
- f(2, 0) vaut 1 (seul rangement confortable :
[[0, 0]]) - f(2, 1) vaut 2, les rangements confortables sont
[[1, 0], [0, 1]] - f(7, 3) vaut 10, ci-dessous tous les rangements confortables possibles :
[1, 0, 1, 0, 1, 0, 0] [1, 0, 1, 0, 0, 1, 0]
[1, 0, 0, 1, 0, 1, 0] [0, 1, 0, 1, 0, 1, 0]
[1, 0, 1, 0, 0, 0, 1] [1, 0, 0, 1, 0, 0, 1]
[0, 1, 0, 1, 0, 0, 1] [1, 0, 0, 0, 1, 0, 1]
[0, 1, 0, 0, 1, 0, 1] [0, 0, 1, 0, 1, 0, 1]
Modifier la fonction récursive de comptage pour qu’elle renvoie la liste de tous les rangements confortables.
91. Équipe minimale ayant tous les talents¶
On dispose d’un ensemble \(\mathtt{E}\) de personnes \(\mathtt{1, 2, \dots, n}\). On considère par ailleurs un ensemble \(\mathtt{A}\) de \(\mathtt{p}\) aptitudes, disons \(\mathtt{A_1, A_2, \dots, A_p}\). Chaque personne de \(\mathtt{E}\) possède un certain nombre d’aptitudes parmi les aptitudes de l’ensemble \(\mathtt{A}\). La totalité des aptitudes est couverte par l’ensemble des personnes dans \(\mathtt{E}\). Ecrire une fonction (récursive) trouver_equipe qui détermine une équipe d’effectif minimal formée d’individus de \(\mathtt{E}\) réunissant toutes les aptitudes de la liste \(\mathtt{A}\).
Par exemple, voici pour \(\mathtt{n=9}\) et \(\mathtt{p=10}\), une répartition d’aptitudes notées, pour alléger, \(\mathtt{A, B, \dots, I, J}\) :
1 ACIJ
2 EFHJ
3 BF
4 C
5 AEG
6 C
7 BCDFJ
8 ABE
9 B
Alors, une équipe d’effectif minimal ayant toutes les aptitudes contient au moins 4 personnes, par exemple :
1 ACIJ
2 EFHJ
5 AEG
7 BCDFJ
Ce problème est celui de la couverture minimale par des ensembles : Wikipedia.
92. Séparer récursivement une nombre par blocs de 3 chiffres¶
On donne un entier N positif sous forme d’une chaîne de caractères s formée exclusivement de chiffres entre 0 et 9, par exemple la chaîne
"14959787070"
On demande d’écrire une fonction récursive blocs(s) renvoyant une chaîne de caractères représentant le même nombre N sauf que ses chiffres sont reproupés par paquets de 3 à partir du chiffres des unités, les blocs étant séparés par des caractères _ (un blanc souligné).
Voici quelques exemples de comportements du programme :
0 → 0
5 → 5
42 → 42
142 → 142
2038 → 2_038
149597870 → 149_597_870
14959787070 → 14_959_787_070
On pourra utiliser des slices. Si on ne connait pas les slices, on pourra écrire une fonction récursive blocs(s, i, j) qui renverra la chaîne avec séparateurs pour le nombre représenté par les chiffres de s entre les indices i (inclus) et j (exclu).
[L’idée de coder la question récursivement revient à Énora.]
93. Eléments d’une liste valant tous zéro ou un¶
Soient L une liste d’entiers et i un indice valide de la liste L. Ecrire une fonction récursive in01(L, i) qui renvoie True si les éléments d’indices inférieurs ou égaux à i de la liste L sont parmi 0 ou 1 et False sinon. En particulier, écrire un appel qui teste si la liste L est formée, oui ou non, d’entiers tous parmi 0 ou 1.
Par exemple, si L = [1, 0, 1, 5, 0] alors `in01(L, 2)` renvoie True et `in01(L, 4)` renvoie False.
94. Premier entier pair (version récursive)¶
Ecrire un fontion récursive premier_entier_pair(L, i) qui à partir d’une liste L d’entiers positifs et d’un indice valide i de cette liste renvoie :
- le premier entier pair présent dans la liste L et à un indice inférieur ou égal à \(\mathtt{i}\)
(-1)s’il n’existe aucun entier pair dans la liste avant l’indicei
Par exemple, pour la liste L = [51, 81, 13, 42, 52, 77, 84] alors
- si
i = 5alors l’appelpremier_entier_pair(L, i)renvoie42 - si
i = 2alors l’appelpremier_entier_pair(L, i)renvoie-1
Une fois la fonction écrite, on utilisera la fonction pour déterminer la présence d’un entier pair dans une liste d’entiers positifs et la valeur de celui présent au plus petit indice si un tel entier existe dans la liste.
95. Pas d’impair (version récursive)¶
Soit une liste L formée d’entiers et \(\mathtt{i\geq 0}\) un indice valide de cette liste. Écrire, une fonction récursive queDesPairs(L, i) et renvoyant True si la liste L ne contient que des entiers pairs entre les indices 0 et i (indices inclus) et False sinon
Par exemple, si L = [82, 32, 48, 81, 42] alors queDesPairs(L, 2) vaut True tandis que queDesPairs(L, 4) vaut False à cause de L[3] = 81 qui est impair.
96. Zéros en fin de liste (version récursive)¶
Ecrire une fonction récursive zeros(L, i) qui, étant donné une liste d’entiers L et un indice i de L renvoie la longueur du bloc de zéros consécutifs se terminant à l’indice i de L. Par exemple, si
L = [2, 3, 0, 1, 0, 0, 0, 0, 4, 0]
alors
- l’appel
zeros(L, 6)vaut 3 carL[6] = L[5]=L[4]=0(ce qui fait 3 zéros consécutifs) et queL[3]!=0, - l’appel
zeros(L, 3)vaut 0 carL[3]!=0.
Ecrire un appel de la fonction zeros(L, i) permettant de déterminer le nombre de zéros situés en fin de la liste L. Par exemple, si L = [3, 5, 0, 0, 0, 0] alors L se termine par 4 zéros.
97. Distance de Hamming (version récursive)¶
Étant donné deux chaînes de caractères s et t, supposées de même longueur, on appelle distance de Hamming entre s et t, le nombre de positions où les chaînes ont des caractères différents. Par exemple, si s et t sont les chaînes
s = "pointes"
t = "voisins"
alors, la distance de Hamming entre ces deux chaînes est 4.
Ecrire une fonction récursive hamming(s, t, k) qui renvoie la distance de Hamming entre les deux chaînes de caractères formée des k premiers caractères de s et des k premiers caractères de t où k est un entier positif ou nul, et s et t deux chaînes de même longueur. Par exemple, si s et t sont les chaînes ci-dessus, alors hamming(s, t, 4) = 2 et hamming(s, t, 6) = 4
Pour finir, écrire un appel qui calcule la distance de Hamming entre deux chaînes de même longueur.
98. Cloner un dossier¶
Les mots dossier et répertoire sont ici synonymes.
On dispose d’un répertoire « source » et d’un répertoire « cible ». On veut « cloner » tous les fichiers et répertoires de la source dans la cible. Ecrire une fonction récursive rcopy(src, dstn) qui effectue cette tâche.
On aura besoin des fonctions décrites ci-dessous :
import os, shutil
# Génère la liste des noms des fichiers et répertoires
# présents dans le répertoire donné (mais pas les sous-répertoires)
base_dir= "./"
for f in os.listdir(base_dir):
print(f)
path="toto.txt"
# teste si un item est un fichier ou pas
# Adresse relative à l'appel
print(os.path.isfile(path))
# copie un fichier de chemin path dans un répertoire dstn
path="./mes_fichiers/toto.txt"
dstn="ma_destn"
shutil.copy(path, dstn)
# Crée un répertoire
my_folder="./mes_fichiers/tres_important"
os.mkdir(my_folder)
# Crée un nom d'item de manière portable
# ne crée pas de fichier, c'est juste un nom
my_folder="./mes_fichiers/important"
mon_fichier="toto.txt"
print(os.path.join(my_folder, mon_fichier))