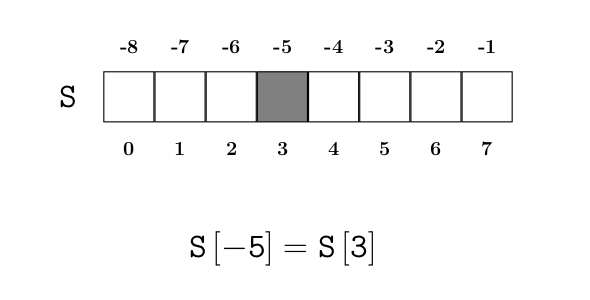Les slices
Slices en lecture¶
Présentation des slices¶
Le terme anglais de slice est associé à l’idée de découpage (une part de gâteau ou de pizza). En programmation, et en Python en particulier, un slice permet le découpage de structures de données séquentielles, typiquement les chaînes de caractères ou les listes.
Les slices sont des expressions du langage Python qui vous permettent en une ligne de code d’extraire des éléments d’une liste ou d’une chaîne. Deux exemples :
- Vous avez une variable
datequi référence une date sous le format jj/mm/aaaa et vous voulez extraire juste le mois de cette date. Avec un slice, vous l’obtiendrez juste avec ceci :date[3:5]. - Vous voulez savoir si un fichier est un fichier python (donc si son nom se termine par l’extension .py) alors vous aurez juste à écrire
nom[-3:]=='.py'et on pourrait, aussi simplement, généraliser au test de n’importe quelle extension de fichier.
L’intérêt des slices est essentiellement la concision et la souplesse de leur syntaxe et le fait qu’elles économisent beaucoup de code (des instructions for ou if, des créations de listes intermédiaires, de la gestion d’indices, etc).
Ce document est paru initialement sur le site zeste de savoir. Merci aux membres jido, yoch (erreur signalée dans la version bêta) et lewoudar.
Un grand merci à Diégo pour avoir réalisé le logo de ce tutoriel.
Slice à deux indices¶
Soit S une séquence, par exemple une chaîne ou une liste. Une expression de la forme S[4:16] est un slice dans sa syntaxe de base. Cette syntaxe utilise deux indices, ici les indices 4 (indice de début du slice) et 16 (indice de fin du slice).
Voici un exemple typique de slice de base :
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
print(alpha[4:16])
EFGHIJKLMNOP
alpha[4:16] est un slice et désigne la chaîne extraite de la chaîne alpha dont les éléments sont situés :
- à droite de l’élément d’indice 4,
- strictement à gauche de l’élément d’indice 16, autrement dit jusqu’à l’indice 15 inclus
ce qui graphiquement donne :
Plus généralement, si i et j sont des indices positifs, la syntaxe S[i:j] désigne la séquence, de même nature que S, formée des éléments S[k] où k vérifie \(i \leq k < j\). Noter l’intervalle entier semi-fermé : le terme d’indice de droite n’est jamais inclus dans le slice obtenu.
Comme toute séquence, un slice a une longueur :
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
s=alpha[4:16]
print(len(s))
12
Un slice peut être vide :
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
s = alpha[10:8]
print(len(s))
0
Type d’un slice¶
Si un slice t est construit à partir d’une séquence s alors t est de même type que s, autrement dit si s est une chaîne alors t est aussi une chaîne, si s est une liste alors t est une liste, etc.
Voici un exemple de slice de base construit sur une liste :
L = [65, 31, 9, 32, 81, 82, 46, 12]
print(L[2:6])
[9, 32, 81, 82]
Les slices s’appliquent essentiellement à des chaînes, des listes et des tuples.
En revanche, les slices étant construits à partir d’indices entiers, ils n’ont pas de sens pour des structures de données non ordonnées comme des dictionnaires ou des ensembles.
Édition d’un slice¶
Dans un slice, des espaces autour du symbole deux-points peuvent ou non être insérées, et on pourra, si on est pointilleux, suivre les recommandations de la PEP 8. Ainsi, on écrira plutôt L[2:6] que L[2 : 6].
Illustration des slices avec deux indices : segmenter un numéro de téléphone¶
Vous voulez segmenter une chaîne de caractères à intervalles réguliers par un séparateur donné ; typiquement, pour un numéro de téléphone, 0942371804 devient 09-42-37-18-04.
Si s est la chaîne, on la découpe en tranches de longueur la période p avec un slice de la forme s[m:m+p] qu’on place ensuite dans une liste en compréhension dont on rassemble les éléments tout en insérant le séparateur avec la méthode join. D’où le code suivant :
def insert_sep(s, sep, period):
return sep.join([s[m:m+period] for m in range(0, len(s), period)])
tel="0942371804"
print(tel, "->", insert_sep(tel, '-',2))
0942371804 -> 09-42-37-18-04
Indices négatifs¶
Les listes admettent aussi une indexation négative. Voici d’abord un exemple :
1 2 3 4 5 | L = [65, 31, 9, 32, 81, 82, 46, 12]
print(L[-5])
print(L[-1])
print(L[-2])
|
6 7 8 | 32
12
46
|
- le 5ème élément avant la fin
- le dernier élément de la liste
- l’avant-dernier élément de la liste
Un indice strictement négatif permet d’accéder à la liste en se référant à la fin de la liste.
Comme pour les indices positifs, le dépassement d’indice est interdit :
1 2 3 | L = [65, 31, 9, 32, 81, 82, 46, 12]
print(L[-15])
|
4 | IndexError: list index out of range
|
- Le 15ème élément de la liste à partir de la fin n’existe pas, donc un message d’erreur est affiché.
Le tableau ci-dessous indique les indices d’éléments remarquables d’une liste \(L\) de longueur \(n\) :
Table: Indices d’éléments remarquables
Élément de L
(liste de longueur n) |
indice positif | indice négatif |
L[i] |
\(\mathtt{0\leq i < n}\) | i-n |
| Premier élément de L | 0 | -n |
| Dernier élément de L | n-1 |
-1 |
| Avant-dernier élément de L | n-2 |
-2 |
On remarquera si un élément d’une liste L est d’indice \(i\geq 0\) et \(j<0\) alors \(i+j=len(L)\).
les indices négatifs s’appliquent non seulement aux listes mais à toute séquence telle qu’une chaîne, un tuple, un objet de type range :
t = (65, 31, 9, 32, 81, 82, 46, 12)
print(t[-5])
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
print(alpha[-5])
r = range(42)
print(r[-5])
32
V
37
Slices et indices négatifs¶
Les indices d’un slice peuvent être des entiers négatifs, la signification étant exactement la même que pour des indices positifs :
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
s = alpha[5:-3]
print(s)
s = alpha[-5:24]
print(s)
s = alpha[-5:-1]
print(s)
FGHIJKLMNOPQRSTUVW
VWX
VWXY
Dépassement d’indice¶
À la différence des séquences, les slices tolèrent le dépassement d’indice, à droite ou à gauche (avec un indice négatif) : les portions du slice qui « dépassent » à droite ou à gauche sont ignorées.
Exemples :
1 2 3 | alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
print(alpha[20:50])
print(alpha[-50:8])
|
4 5 | UVWXYZ
ABCDEFGH
|
- Ligne 2 : comme
50 > len(alpha) = 26, c’est comme si on avait écrits = alpha[20:26]. - Lignes 3 : la chaîne est en fait identique à
alpha[-26:8].
Omission d’indice¶
Quand un slice se réfère à une des deux extrémités de la séquence, un raccourci syntaxique permet d’omettre l’indice de début ou de fin. Par exemple, le slice s[:j] est synonyme de s[0:j] (que l’indice soit positif ou non).
Voici des exemples typiques :
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
## Les 5 premiers
print(alpha[:5])
## Les 5 derniers
print(alpha[-5:])
## Tous sauf les 5 premiers
print(alpha[5:])
## Tous sauf les 5 derniers
print(alpha[:-5])
ABCDE
VWXYZ
FGHIJKLMNOPQRSTUVWXYZ
ABCDEFGHIJKLMNOPQRSTU
Il est même possible d’ignorer les deux indices. Le slice s[:] est alors défini comme s[0:n] où n est la longueur de s :
L = [81, 42, 31, 12]
M = L[:]
print(L)
print(M)
[81, 42, 31, 12]
[81, 42, 31, 12]
Le slice s[:] crée ce qu’on appelle une copie superficielle de s.
Slices étendus¶
La syntaxe des slices admet une extension autorisant un 3e entier entre les crochets : s[i:j:k]. Cet entier k désigne un pas (step en anglais), comme quand on compte par pas de k, par exemple de 3 en 3.
Exemple :
1 2 3 | alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
s = alpha[4:23:3]
print(s)
|
4 | EHKNQTW
|
- Lignes 2 et 4 :
sest la chaîne formée des éléments de la chaînealphad’indices allant de 3 par 3 entre l’indice 4 inclus et l’indice 23 exclu.
L’exemple ci-dessus en visuel :
Le pas d’un slice ne peut être nul sinon une exception est levée.
Slice étendu ayant son 3e indice négatif¶
Si dans le slice s[i:j:k], l’entier k est négatif, on compte de -k en -k en arrière à partir de la position d’indice i. Par exemple :
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
s = alpha[23:4:-3]
print(s)
XUROLIF
Si l’indice j correspond à une position à droite de i, le slice sera vide :
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
s = alpha[4:23:-3]
print(s)
# Aucun sortie visible
Slice étendu et omission d’indices¶
Étant donné un slice L[a:b:c] ayant trois emplacements pour des indices, il est possible de ne pas indiquer certains indices. Voici des exemples :
s = "0123456789"
print("s[3:7:] ->", s[3:7])
print("s[:7:2] ->", s[:7:2])
print("s[3::2] ->", s[3::2])
print("s[:3:-2] ->", s[:3:-2])
print("s[7::-2] ->", s[7::-2])
qui affiche
s[3:7:] -> 3456
s[:7:2] -> 0246
s[3::2] -> 3579
s[:3:-2] -> 975
s[7::-2] -> 7531
Si comme pour le slice L[a:b:], le dernier indice est omis, il vaut implictement 1 et en fait c’est comme si on avait écrit L[a:b].
Lorsque le premier ou le deuxième sont omis, cela dépend du signe du troisième et dernier indice (qu’il soit explicite ou omis) :
si le dernier indice est strictement positif,
- le premier indice, s’il est omis, vaut implicitement 0
- le dernier indice, s’il est omis, vaut implicitement
len(L)
si le dernier indice est strictement négatif,
- le premier indice, s’il est omis, vaut implicitement -1
- le dernier indice, s’il est omis, vaut implicitement
-len(L) - 1.
Idiomes utilisant des slices étendus¶
Comme pour les slices avec deux indices, les indices peuvent être négatifs et/ou absents. Voici des formes très utilisées en pratique :
L = [10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25]
## de 5 en 5 depuis l'indice 4
# -> [14, 19, 24]
print(L[4::5])
## de 3 en 3 entre le 5ème et le 2ème avant la fin
# -> 15, 18, 21]
print(L[5:-2:3])
## extraire de 5 en 5
# -> [10, 15, 20, 25]
print(L[::5])
## extraire de 5 en 5 à partir de la fin
# -> [25, 20, 15, 10]
print(L[::-5])
## éléments d'indices pairs
# -> [10, 12, 14, 16, 18, 20, 22, 24]
pairs = L[::2]
print(pairs)
## éléments d'indices impairs
# -> [11, 13, 15, 17, 19, 21, 23, 25]
impairs = L[1::2]
print(impairs)
Slice de pas -1¶
Un cas particulier très pratique est l’inversion de séquence avec un slice de pas valant \(-1\) :
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
s = alpha[23:4:-1]
print(s)
XWVUTSRQPONMLKJIHGF
En particulier, s[::-1] renvoie la séquence complète inversée :
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
s = alpha[::-1]
print(s)
ZYXWVUTSRQPONMLKJIHGFEDCBA
Illustration des slices étendus : détection de palindrome¶
Un palindrome est un mot qui est identique qu’il soit lu de gauche à droite ou de droite à gauche. Un slice de pas -1 permet d’écrire une fonction de détection de palindrome :
def isPalindrome(s):
return s == s[::-1]
print(isPalindrome("aziza"))
True
Tableau des idiomes les plus importants sur les slices¶
Le tableau suivant résume ce que l’on utilise des slices dans \(80\%\) de la pratique.
Action sur la
séquence s |
Code | Exécution
(s = "ABCDEFGHIJKL") |
| Extraction | s[2:7] |
CDEFG |
| Copie superficielle | s[:] |
ABCDEFGHIJKL |
| Les 4 premiers | s[:4] |
ABCD |
| Les 4 derniers | s[-4:] |
IJKL |
| Tous sauf les 4 premiers | s[4:] |
EFGHIJKL |
| Tous sauf les 4 derniers | s[:-4] |
ABCDEFGH |
| Partitionner | s[:3], s[3:7], s[7:] |
('ABC', 'DEFG', 'HIJKL') |
| De 3 en 3 | s[::3] |
ADGJ |
| De 3 en 3 à partir de la fin | s[::-3] |
LIFC |
| Les indices pairs | s[::2] |
ACEGIK |
| Les indices impairs | s[1::2] |
BDFHJL |
| Copie superficielle | s[::] |
ABCDEFGHIJKL |
| Copie à l’envers | s[::-1] |
LKJIHGFEDCBA |
Slices de type range¶
Les objets de type range (comme range(42)) sont des séquences et prennent donc en charge les slices. On peut ainsi écrire des slices de range comme on le ferait pour des chaînes :
r = range(10, 25)
print(r[2:8])
print(r[::-1])
range(12, 18)
range(24, 9, -1)
Un slice de range est encore de type range. Ce type de slice est peu usité.
Slices en écriture¶
Modifier une liste avec un slice¶
La syntaxe des slices permet aussi de modifier une liste suivant une tranche :
L = [10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
T = "ABCD"
L[2:8] = T
print(L)
[10, 11, 'A', 'B', 'C', 'D', 18, 19]
Si L est une liste et si M un itérable quelconque alors l’affectation L[i:j] = M est effectuée ainsi :
- tous les éléments de
Laux positionsrange(i, j)sont retirés de la listeL; - les éléments de l’itérable
Msont insérés à partir de l’endroit où les éléments ont été retirés.
Pour ne pas se tromper d’indice, remarquer que l’indice du 1er élément inséré est exactement le 1er indice du slice :
L = [10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
T = "ABCD"
g = 2
L[g:8] = T
print(L[g])
A
On peut utiliser cette technique pour remplacer le contenu d’une liste donnée :
L=[]
L[:]=range(5)
print(L)
[0, 1, 2, 3, 4]
L’opération L[:] correspond sur une liste à une action d’effacement avec clear suivie d’une extension avec extend :
L=[42, 45, 81, 39]
print(L, id(L))
temp=[2038, 2040]
L[:]=temp
print(L, id(L))
L=[42, 45, 81, 39]
print(L, id(L))
L.clear()
L.extend(temp)
print(L, id(L))
[42, 45, 81, 39] 140691544257728
[2038, 2040] 140691544257728
[42, 45, 81, 39] 140691519628800
[2038, 2040] 140691519628800
Slices à deux indices : idiomes de complétion et suppression¶
Voici, résumé en code, quelques actions de complétion ou de suppression :
## Insérer sans supprimer
L = [10, 11, 12, 13, 14, 15]
L[3:3] = "ABC"
print(L)
## -> [10, 11, 12, 'A', 'B', 'C', 13, 14, 15]
## Étendre L
L = [10, 11, 12, 13, 14, 15]
L[len(L):] = "ABC"
print(L)
## [10, 11, 12, 13, 14, 15, 'A', 'B', 'C']
## Effacer une tranche
L = [10, 11, 12, 13, 14, 15]
L[1:4] = []
print(L)
## -> [10, 14, 15]
## Suppression d'une tranche avec del
L = [10, 11, 12, 13, 14, 15]
del L[1:4]
print(L)
## -> [10, 14, 15]
Remplacement et suppression avec des slices étendus¶
Comme avec des slices à deux indices, des modifications de listes sont possibles avec des slices étendus. Résumé en code :
## Remplacer
L = [10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
print(L[1:8:2]) # -> [11, 13, 15, 17]
L[1:8:2] = "ABCD"
print(L)
## -> [10, 'A', 12, 'B', 14, 'C', 16, 'D', 18, 19]
## Supprimer
L = [10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
del L[1:8:2]
print(L)
## -> [10, 12, 14, 16, 18, 19]
Slice en écriture et non-concordance de taille¶
Lorsqu’on utilise un slice pour écriture dans une liste, la taille du slice et et le nombre d’éléments du remplacement doivent correspondre sinon une exception est levée :
L = [10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
L[1:8:2] = "ABC"
print(L)
ValueError: attempt to assign sequence of size 3 to extended slice of size 4
Illustration des slices étendu en écriture : le crible d’Ératosthène¶
Un exemple d’application remarquable de la modification d’une liste avec des slices est le crible d’Ératosthène.
Le crible d”Ératosthène permet de lister tous les nombres premiers entre 1 et \(n\) où \(n\) est donné. Le principe de ce crible est que l’on part d’une liste L des entiers entre 0 et \(n\) et on crible L (autrement dit, on raye de L) les multiples de \(d\) pour certains \(d\) bien choisis en sorte que, à la fin du criblage de L, il ne reste plus que des nombres premiers dans L. En pratique, l’implémentation informatique est un peu différente car
- au lieu d’utiliser la liste
Ldes entiers entre 0 et \(n\) on utilise une listecribleindexée de 0 à \(n\) (cf. le code ci-dessous), contenant des booléens et qui indiquent, à chaque indice \(i\), si l’entier \(i\) est premier (True) ou non (False) ; - pour cribler, on change un
TrueenFalsedans la liste.
Naturellement, le fait de cribler des multiples de \(d\) dans une liste fournit une utilisation presque idéale des slices étendus.
Voici le crible avec des slices en action :
1 2 3 4 5 6 7 8 9 10 11 12 | def eratosthene_slice(n):
crible=[False,False]+[True]*(n-1)
for d in range(int(n**0.5)+1):
if crible[d]:
crible[d*d::d]=[False]*(n//d -d+1)
return crible
c=eratosthene_slice(50)
for i in range(len(c)):
if c[i]:
print(i, end= ' ')
print()
|
13 | 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47
|
- Lignes 1-6 : La fonction renvoie une liste qui sera le crible d’Ératosthène indiquant les entiers premiers entre 0 et \(n\) (inclus).
- Ligne 2 : la liste qui va être criblée. Ce n’est pas la liste des entiers jusqu’à \(n\) mais une liste de booléens indexée de 0 à \(n\) (et contenant donc \(n+1\) entiers).
- Ligne 2 : au départ, tout le monde est considéré comme premier, sauf 0 et 1 d’où les deux premiers
Falsede la liste. - Ligne 3 : toute l’efficacité de la méthode du crible est dans la racine carrée \(\sqrt n\).
- Ligne 4-5 : on peut montrer que l’exécution ne passe la condition
ifque sidest premier. - Ligne 5 : c’est ici le cœur du programme, là où intervient le criblage et le slice. Comme tout multiple de
d(distinct ded) est, bien entendu, non premier, il faut basculer àFalsetous les booléens situés aux indices multiples de \(d\) entre \(d^2\) et \(n\). Pourquoi pas avant \(d^2\) ? Parce ces multiples ont déjà été rayés à une étape précédente de la bouclefor. - Ligne 5 : un point délicat du programme ; pour avoir la bonne taille du slice cible, il faut soigneusement compter le nombre de multiples \(m\) de \(d\) tels que \(d^2\leq m\leq n\) et on trouve assez facilement
n//d -d+1. - Ligne 9 : pour rendre le code plus accessible,
enumeraten’a pas été utilisé.
On peut légèrement optimiser l’algorithme en criblant séparément les entiers pairs en sorte qu’il suffit ensuite (pour \(\mathtt{d\geq 3}\) dans la boucle) de cribler un multiple sur deux (uniquement les multiples impairs de \(\mathtt{d}\)), ce qui donne :
1 2 3 4 5 6 7 8 9 10 11 12 13 | def eratosthene_slice(n):
crible=[False,False]+[True]*(n-1)
crible[4::2]=[False]*(n//2 -1)
for d in range(3, int(n**0.5)+1, 2):
if crible[d]:
crible[d*d::d]=[False]*(n//d -d+1)
return crible
c=eratosthene_slice(50)
for i in range(len(c)):
if c[i]:
print(i, end= ' ')
print()
|
14 | 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47
|
- Ligne 3 : on crible les entiers pairs ; c’est exactement le code de la ligne 6 avec
d=2. - Ligne 4 : on ne crible que les multiples impairs de
d, les multiples pairs ayant ayant été criblés ligne 3.
Illustration des slices étendus : extraction de diagonales¶
On se donne un tableau 2D de \(n\) lignes et de \(p\) colonnes et on demande de déterminer le contenu d’une diagonale donnée. On va se limiter aux diagonales descendantes. Pour se repérer, la diagonale principale, celle qui commence en haut à gauche, est indexée par 0. Ensuite chaque diagonale en-dessous de (ou égale à) la diagonale principale est repérée par un indice dans range(n), et au-dessus, par un indice de range(p). Par exemple, dans la grille ci-dessous :
la diagonale d’indice 3 au-dessus de la diagonale principale est : B, E, O, E, U, S :
Pour déterminer le contenu d’une diagonale, il suffit de remarquer que, si on convertit le tableau 2D (disons T) en son équivalent 1D (disons L) suite à un parcours par lignes, chaque élément de la diagonale cherchée est placé à des indices de L qui sont régulièrement espacés, plus précisément de \(p+1\). Ensuite, après un éventuel petit calcul, on détermine quand il faut s’arrêter dans L pour ne pas sortir du tableau T. D’où le code :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | T =[
'REABRASES',
'ENCRENENT',
'OCTOCORDE',
'RAVAUDERA',
'CHICORIUM',
'EPARTIRAS',
'RENIERONS',
'ALTERANTE',
'SASSASSES']
L = [c for line in T for c in line]
n = len(T)
p = len(T[0])
# Diagonales au-dessus de la diagonale principale
for k in range(p):
diago = L[k:p*min(n,p-k):p+1]
print(' '.join(diago))
print()
# Diagonales en-dessous de la diagonale principale
for k in range(n):
diago = L[k*p:p*min(n,p+k):p+1]
print(' '.join(diago)
|
27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | R N T A O I O T S
E C O U R R N E
A R C D I A S
B E O E U S
R N R R M
A E D A
S N E
E T
S
R N T A O I O T S
E C V C T R N E
O A I R E A S
R H A I R S
C P N E A
E E T S
R L S
A A
S
|
- Ligne 12 : extraction (« applatissement ») du tableau 2D ligne par ligne en une liste
L. - Lignes 18-20 et 24-26 :
kreprésente l’indice de la diagonale que l’on va afficher. Rappel : l’indice zéro est celui de la diagonale principale. - Lignes 18-20 : c’est le cas le plus facile. Il est immédiat que l’on se déplace de \(p+1\) en \(p+1\) dans L (pour le voir, lire les déplacements sur le tableau 2D). Le début du slice est clairement
k. La fin du slice se devine car les indices dansLde la première colonne deTsont les multiples dep. - Lignes 24-26 : c’est très analogue.
Slices personnalisés¶
Syntaxe complète des slices¶
La syntaxe qu’on a rencontrée, et qui est la plus courante pour un slice, est de la forme s[i:j] ou s[i:j:k], les indices i, j et k pouvant être omis. Cependant, la syntaxe complète d’une opération de slicing offre davantage de possibilités. Ainsi, un code pourrait contenir la syntaxe suivante :
ma_seq[12, 10:(14, 22):-2, (5,33), 2:]
Cette syntaxe curieuse est bien celle d’un slice. La principale différence de la syntaxe complète avec la syntaxe antérieure est que
- il peut y avoir plusieurs slices entre les crochets ; dans l’exemple ci-dessus, on en compte 4, séparés par des virgules ;
- les « indices » ne sont plus forcément entiers ; dans l’exemple ci-dessus, on dispose ainsi de l”« indice »
(5,33).
Chacun de ces « items » placés entre les crochets et séparés par des virgules, peut avoir deux formes :
- des expressions, ci-dessus 12 ou encore le tuple
(5, 33); - des slices « propres », ci-dessus
10:(14, 22):-2ou encore2:(qui contiennent une ou deux fois le symbole deux-points et appelés proper slice dans la documentation officielle).
Cependant, tout type de séquence ne supporte pas cette syntaxe ; par exemple, pour une liste :
L = [65, 31, 9, 32, 81]
print(L[1:3, 2:4])
print(L[1:3, 2:4])
TypeError: list indices must be integers, not tuple
En effet, et c’est la clé de personnalisation des slices, la sémantique d’un slice est déterminée par la méthode __getitem__ de la séquence appelée ; or, dans l’exemple ci-dessus, la méthode __getitem__ de la classe list n’accepte entre des crochets d’indexation :
- soit qu’une seule expression, par exemple
L[3]; - soit qu’un seul slice propre, par exemple
L[2:4].
Cependant, dans l’idée de créer des slices personnalisés, vous pouvez définir une classe puis créer (ou surcharger) la méthode __getitem__ de cette classe afin de pouvoir utiliser la syntaxe complète des slices sur des instances de votre classe. Voici un exemple sans intérêt sauf d’illustrer la syntaxe :
class Ma_seq:
def __getitem__(self, index):
print(index)
ma_seq = Ma_seq()
ma_seq[12, 10:(14, 22):-2, (5,33), 2:]
(12, slice(10, (14, 22), -2), (5, 33), slice(2, None, None))
Le type slice¶
Observons le code suivant :
1 2 3 4 5 | alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
s = alpha[5::4]
t = alpha[slice(5, None, 4)]
print(s)
print(t)
|
6 7 | FJNRVZ
FJNRVZ
|
- Ligne 3 : noter l’appel à la mystérieuse fonction
slice. - Lignes 2 et 3 : noter les analogies.
Lorsqu’un slice tel que s[3::2] est créé, en réalité, Python appelle s[slice(3, None, 2)] où slice est une fonction built-in de Python.
Noter que si l’indice de slice est implicite, on peut le remplacer par None. D’ailleurs, c’est même valable dans un slice avec la syntaxe habituellle :
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
s = alpha[5:None:4]
print(s)
FJNRVZ
La fonction slice est en fait le constructeur de la classe du même nom. Comme on s’y attend, un objet de la classe slice possède des attributs désignant le début(start), la fin (stop) et le pas (step) du slice :
s = slice(5, None, 4)
print(s.start, s.stop, s.step)
5 None 4
Habituellement, ces attributs ont des valeurs entières mais rien n’y oblige, par exemple, ci-dessous, un des « indices » est un tuple :
s = slice(10, (14, 22), -2)
print(s.stop)
(14, 22)
Slice générique¶
On peut utiliser le retour de slice pour « habiller » une extraction valable pour toute séquence. Par exemple, le code ci-dessous permet d’extraire les éléments d’indices impairs de n’importe quelle séquence :
impairs = slice(1, None, 2)
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
print(alpha[impairs])
L = [10, 11, 12, 13, 14, 15]
print(L[impairs])
BDFHJLNPRTVXZ
[11, 13, 15]
Slices personnalisés¶
Illustration préliminaire : concaténation de slices¶
Pour comprendre comment on peut créer des slices personnalisés, on va présenter la méthode sur un exemple complet mais simple.
Construisons une classe nommée StrMultipleSlices, qui hérite de la classe str et dont les slices agiront comme le montre l’extrait de code suivant :
1 2 3 4 | ## Code de StrMultipleSlices omis
alpha = StrMultipleSlices("ABCDEFGHIJKLMNOPQRSTUVWXYZ")
print(alpha[5:9, 5, 10:4:-1, 20:])
|
5 | FGHI-F-KJIHGF-UVWXYZ
|
- Ligne 4 : la classe permet d’utiliser des slices dans leur syntaxe complète.
- Lignes 4 et 5 : l’action d’un slice sur une chaîne
alphade typeStrMultipleSlicesrenvoie la concaténation des différents slices placés entre crochets après les avoir séparés par un tiret.
Voici le code complet commenté de la classe StrMultipleSlices :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | class StrMultipleSlices(str):
def __getitem__(self, slide_list):
try:
return super().__getitem__(slide_list)
except TypeError:
S=[]
for slide_item in slide_list:
S.append(super().__getitem__(slide_item))
return '-'.join(S)
alpha = StrMultipleSlices("ABCDEFGHIJKLMNOPQRSTUVWXYZ")
print(alpha[5:9, 5, 10:4:-1, 20:])
|
15 | FGHI-F-KJIHGF-UVWXYZ
|
- Ligne 1 : la classe hérite de la classe
stren sorte qu’on va effectuer des slices de chaînes. - Ligne 3 : pour obtenir des slices personnalisés, on surcharge la méthode
__getitem__. - Ligne 14 : lorsque le slice est appelé, c’est un tuple de 4 élements qui est envoyé à
__getitem__via le paramètreslide_list(ligne 5). Ainsi, les deux premiers éléments de ce tuple sont :slice(5, 9, 1)et5. - Ligne 5 : en cas de slice unique, on laisse agir les slices de la classe mère
str. - Lignes 6-9 : sinon, une exception est levée et on laisse agir séparément les slices de la classe
str(cf.super()ligne 9) tout en plaçant chaque slice obtenu dans une liste (cf.appendligne 9). - Lignes 11 et 15 : il ne reste plus qu’à concaténer les chaînes de la liste en les séparant par un tiret.
Création de slices personnalisés¶
La connaissance du mécanisme de génération d’un slice permet de créer des slices personnalisés. Lorsqu’un slice dans sa syntaxe complète s[slice_list] est créé, alors
- si
slice_listne contient qu’un seul slice, comme dans le slices = alpha[5::4]alorsslice_listest converti avec la fonction standardsliceet l’objet de type slice obtenu est passé en argument às.__getitem__; - si
slice_listcontient plusieurs items slice, comme dansma_seq[12, 10:14:-2, (5,33), 2:]qui contient 4 items slice, chaque slice propre (comme10:14:-2) est converti en objet de type slice et chaque expression (comme12) est laissée intacte et, après conversion, les items slice sont passés en argument sous forme de tuple às.__getitem__.
Dans tous les cas, le retour de s.__getitem__ détermine la valeur du slice.
Illustration des slices personnalisés : périodes dans une année¶
On va créer une classe Annee représentant une année donnée en argument à la classe, par exemple Annee(2038). Cette classe représentera une séquence de jours et permettra de déterminer, en utilisant la syntaxe des slices, tous les jours entre deux dates données. Voici un exemple d’utilisation de la classe Annee:
1 2 3 4 5 6 | ## code de Annee omis
a=Annee(2038)
print(a[(22, 2):(5, 3):2])
print(a[(25,12):])
print(a[14,7])
|
7 8 9 | [(22, 2), (24, 2), (26, 2), (28, 2), (2, 3), (4, 3)]
[(25, 12), (26, 12), (27, 12), (28, 12), (29, 12), (30, 12), (31, 12)]
(14, 7)
|
- Ligne 3 : une instance représentant l’année 2038.
- Ligne 4 : la syntaxe d’un slice dont les indices sont des jours ; ici, on liste les jours de 2 en 2 entre le 22 février 2038 et le 4 mars 2038 inclus. Noter (ligne 7) que le mois de février s’arrête le 28 en 2038 (année non bissextile) et donc le surlendemain est bien le 2 mars.
- Ligne 5 : idem pour les jours de l’année après Noël 2038 avec un indice implicite.
- Ligne 6 : appliqué à un unique jour, le slice renvoie le jour en question (ligne 9).
Afin de limiter les calculs, le code de Annee utilise la classe date du module standard datetime de gestion des dates.
Le principe d’obtention des jours entre les deux dates données et avec un pas donné utilisé par la classe Annee est le suivant :
- grâce au module
datetime, les deux jours du slice sont convertis en deux « numéros » (le terme exact est « ordinaux ») ; - on appelle ensuite la fonction
rangesur ces numéros et avec le pas pour obtenir les numéros des jours de l’intervalle ; - enfin, à nouveau avec l’aide du module
datetime, on reconvertit ces numéros en jours.
Voici maintenant le code complet et commenté de la classe Annee :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | from datetime import date
class Annee:
def __init__(self, an):
self.an = an
self.debut_ordinal=date(an, 1,1).toordinal()
self.fin_ordinal=date(an+1, 1,1).toordinal()
def __getitem__(self, index):
if isinstance(index, slice):
start, stop, step = index.start, index.stop, index.step
an=self.an
start=(date(an, start[1], start[0]).toordinal()
if start is not None else self.debut_ordinal)
stop=(date(an, stop[1], stop[0]).toordinal()
if stop is not None else self.fin_ordinal)
if step is None:
step=1
return [(date.fromordinal(num).day, date.fromordinal(num).month)
for num in range(start, stop, step)]
else:
return index
a=Annee(2038)
print(a[(22, 2):(5, 3):2])
print(a[(25,12):])
print(a[14,7])
|
29 30 31 | [(22, 2), (24, 2), (26, 2), (28, 2), (2, 3), (4, 3)]
[(25, 12), (26, 12), (27, 12), (28, 12), (29, 12), (30, 12), (31, 12)]
(14, 7)
|
- Lignes 5 et 25 : une instance de
Anneenécessite de connaître l’année. En fait, deux instances ne diffèrent au plus que par un 29 février absent ou présent. - Ligne 8 : À cause de slices de la forme
a[(25,12):](cf. ligne 27), on a besoin de calculer le numéro correspondant au premier janvier de l’année suivante. - Lignes 25-28 : si on calcule un slice sur un objet de type
Annee, la méthode__getitem__(ligne 10) est appelée et le paramètreindexest de typeslice. - Lignes 20-21 :
__getitem__renvoie une liste de jours calculée avec les méthodesfromordinalettoordinal. - Lignes 14-15 et 16-17 : chaque ligne est une expression conditionnelle (opérateur ternaire de Python). La syntaxe Python autorise à écrire une expression sur plusieurs lignes si l’expression est entourée de parenthèses. Comme les deux lignes étaient longues, j’ai utilisé cette possibilité.
- Lignes 14-17 : chaque « indice » du slice est un tuple
(jour, mois), cf. par exemple le tuplestartavecstart[1]etstart[0]ligne 14. - Lignes 14-17 : chaque date est convertie successivement en le type
datededatetimepuis en ordinal. - Lignes 14-17 : chacune des expressions conditionnelles (les deux
if ... else ...) permet de gérer un slice implicite qui commence en début d’année (cf. l’attributdebut_ordinal) ou se termine en fin d’année (cf. l’attributfin_ordinal). - Lignes 16 et 17 : si le troisième indice de slice est absent, le slice s’assimile à un slice de base et cela signifie que le pas est de 1.
- Lignes 30 et 31 : pour un calcul de slice entre deux jours, la liste des jours est renvoyée. Un jour est présenté sous la forme d’un tuple jour et mois.
Illustration des slices personnalisés : sous-matrice¶
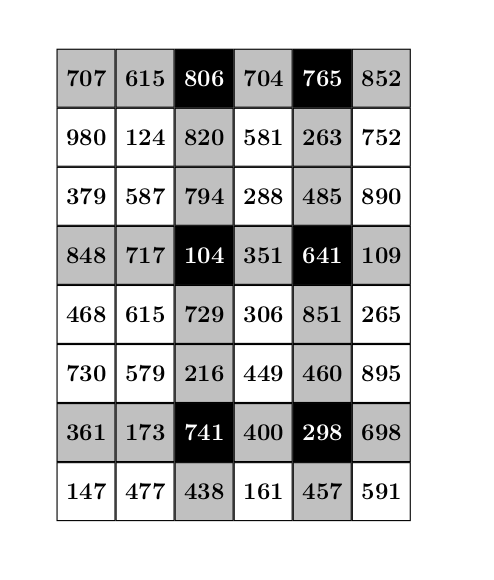
Par matrice, on entend ici un simple tableau \(\mathtt{n\;x\; n}\) de nombres entiers. On veut créer une classe représentant des matrices et permettant d’extraire, avec la syntaxe des slices, une sous-matrice dont les éléments sont régulièrement espacés sur les lignes et les colonnes de la matrice initiale.
Par exemple, on dispose de la matrice \(M\) suivante :
et on veut extraire la sous-matrice telle que
- ses lignes sont les lignes de \(M\), extraites 3 par 3 en commençant à l’avant-dernière ligne,
- ses colonnes sont les colonnes d’indices pairs à partir de la 2e colonne.
On cherche donc à extraire les éléments marqués en noir ci-dessous :
Voici un exemple de fonctionnement du programme et son affichage :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | ## Code de Matrix omis
array=[
[707, 615, 806, 704, 765, 852],
[980, 124, 820, 581, 263, 752],
[379, 587, 794, 288, 485, 890],
[848, 717, 104, 351, 641, 109],
[468, 615, 729, 306, 851, 265],
[730, 579, 216, 449, 460, 895],
[361, 173, 741, 400, 298, 698],
[147, 477, 438, 161, 457, 591]
]
M=Matrix(array)
print(M[-2::-3, 2::2])
|
16 17 18 | 741 298
104 641
806 765
|
- Ligne 15 : observer les deux slices entre les crochets.
Pour parvenir au résultat, on crée une classe Matrix et on va lui implémenter la méthode __getitem__.
L’implémentation va permettre d’extraire aussi bien un élément de la matrice qu’une sous-matrice. Plus précisément, pour extraire par exemple l’élément à la ligne d’indice 5 et à la colonne d’indice 3, on écrira M[5, 3]. Pour extraire une sous-matrice, on utilisera la syntaxe de slice, par exemple M[-2::-3, 2::2]. Il est également possible de panacher les deux notations, par exemple M[5, 1:4].
Voici le code complet et commenté :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 | class Matrix:
def __init__(self, array):
self.nlines = len(array)
self.ncols = len(array[0])
self.array=[list(array[j]) for j in range(self.nlines)]
def __getitem__(self, index):
I=[None, None]
for i, item in enumerate(index):
if isinstance(item, slice):
I[i]=item
else:
I[i]=slice(item, item+1, 1)
M = self.array
n = self.nlines
p = self.ncols
ind_lines = range(n)[I[0]]
ind_cols = range(p)[I[1]]
sub_array =[[M[i][j] for j in ind_cols] for i in ind_lines]
return Matrix(sub_array)
def __str__(self):
return '\n'.join([' '.join(map(str, self.array[i]))
for i in range(self.nlines)])
array=[
[707, 615, 806, 704, 765, 852],
[980, 124, 820, 581, 263, 752],
[379, 587, 794, 288, 485, 890],
[848, 717, 104, 351, 641, 109],
[468, 615, 729, 306, 851, 265],
[730, 579, 216, 449, 460, 895],
[361, 173, 741, 400, 298, 698],
[147, 477, 438, 161, 457, 591]
]
M=Matrix(array)
print(M)
print()
print(M[-2::-3, 2::2])
print()
print(M[5, 1:4])
print()
print(M[5, 3])
|
48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 | 707 615 806 704 765 852
980 124 820 581 263 752
379 587 794 288 485 890
848 717 104 351 641 109
468 615 729 306 851 265
730 579 216 449 460 895
361 173 741 400 298 698
147 477 438 161 457 591
741 298
104 641
806 765
579 216 449
449
|
- Lignes 4-6 : on passe un tableau 2x2 (une liste de listes) à la matrice (ligne 38) et on en extrait, dans des attributs, les dimensions de la matrice ainsi que ses coefficients.
- Ligne 9 : par défaut, et pour simplifier, on suppose qu’entre les crochets de slices, on passe toujours à
Mune suite d’exactement 2 items (la taille deI), séparés par une virgule (attention, cette suite est juste de la syntaxe et, bien qu’en ayant l’apparence, ce n’est pas un tuple et ce n’est même pas un objet). Pour un code plus robuste, il faudrait capturer dans untry/exceptun nombre éventuellement incorrect d’items de slice. - Lignes 10 et 14 : chacun des deux items est transformé en objet de type
sliceet placé dans une liste. - Lignes 18 et 19 : on peut ensuite facilement extraire les indices de lignes et de colonnes recherchés en appliquant ces slices aux
rangedes nombres de lignes et de colonnes. - Lignes 23-25 : on implémente une méthode simpliste d’affichage mais qui donne des alignements corrects si les coefficients de la matrice sont des entiers ayant tous le même nombre de chiffres.
Ce type de slices est implémenté dans le logiciel mathématique Sagemath et, avec une plus grande envergure, dans la bibliothèque de calcul numérique NumPy.
Annexe¶
Les slices dans la documentation officielle¶
La documentation officielle est peu prolixe sur les slices (mais le sujet n’est pas si vaste). Pour une connaissance en profondeur, les points importants à lire sont les suivants :
- le type slice,
- la méthode spéciale getitem,
- la syntaxe des slicings, sans doute la partie la moins abordable,
- la description de la classe built-in slice,
- la description de la fonction itertools.islice.
Copie ou pas ?¶
Lorsqu’on effectue un slice (disons t) d’une liste ou d’un tuple (disons s), le contenu de s n’est jamais recopié. Les contenus de s et de t réfèrent aux mêmes objets, simplement lors de la création de t, des références vers les éléments du slice ont été créées. Autrement dit, une séquence s et un slice de s partagent les mêmes contenus.
Le message suivant, toujours d’actualité, confirme la réalisation d’une copie de références : Stack Overflow
Voici une illustration commentée :
1 2 3 4 5 6 7 8 9 10 | from random import randrange
N=100
L = [randrange(100,1000) for _ in range(N)]
g, d = 42, 87
S = L[g:d]
for _ in range(5):
i = randrange(g, d)
print(L[i] is S[i-g])
|
11 12 13 14 15 | True
True
True
True
True
|
- Ligne 4 : on construit une liste
Ld’entiers aléatoires entre 100 et 1000 [on choisit des entiers valant au moins 100 pour éviter l’effet de cache utilisé par défaut par Python sur les petits nombres]. - Ligne 5 : on construit un slice
Ssur la listeLentre les indices g (pour gauche) et d (pour droit). - Lignes 8-9 : on génère aléatoirement 5 entiers dans le slice
S. - Ligne 10 : on compare, non pas la valeur, mais l”identité de chacun des objets choisis dans le slice avec l’identité des éléments correspondants dans
L. - Lignes 11-15 : on constate que les identités sont les mêmes : il n’y a pas eu de copie d’objet, juste copie de références.
Le cas des chaînes est différent. En effet, il se trouve que si s est une chaîne, alors toute indexation s[k], où s[k] est un caractère unicode d’ordinal à partir de 256, crée un nouveau caractère de valeur identique, cf. le code source de CPython :
if (max_char >= 256)
memcpy(PyUnicode_2BYTE_DATA(res), u, sizeof(Py_UCS2)*size);
Comme toute opération de slicing sur une séquence effectue implicitement une indexation, tout slicing de chaîne recrée les caractères de la chaîne. Le code suivant illustre les changements :
1 2 3 4 5 | D=1000
s = ''.join(chr(x) for x in range(D,D+3))
a, b, c = s[:]
print(s[0] == a)
print(s[0] is a)
|
6 7 | True
False
|
- Ligne 1 : l’ordinal des caractères unicodes doit dépasser 256 (ici, à partir de 1000).
- Ligne 3 :
aest le premier item d’un slice des. - Lignes 4 et 5 : les deux caractères ont même valeur mais ne sont pas les mêmes en mémoire (le caractère référencé par
aest nouveau).
Le fait qu’un slice effectue une copie de sous-chaîne est confirmé par ce message sur SO ainsi que ce message plus ancien.
Coût d’un slice¶
Si s est un slice construit à partir d’une liste t, alors la création de s nécessite la copie de références vers les éléments de t que s référence. Par exemple, si t est une liste d’un million d’entiers alors t[:] va créer un million de références vers les éléments de t, comme cela est confirmé le code source de CPython. La documentation officielle ne précise pas ce point. Toutefois Tim Peters qui est un Python core developper historique l’indique dans ce message.
Examinons, à travers deux exemples, le coût de la création d’un slice.
Coût modéré¶
Les slices restent un outil très efficace et l’expérience montre que le coût de création d’un slice est relativement peu élevé par rapport aux opérations réellement effectuées.
Par exemple, comparons ces deux façons de faire pour calculer manuellement le maximum des éléments d’une liste de 50 millions d’entiers :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | from time import perf_counter
N = 5 * 10 ** 7
L = list(range(N))
begin_perf = perf_counter()
maxi1 = L[0]
for x in L:
if x > maxi1:
maxi1 = x
print("%.3fs" % (perf_counter() - begin_perf))
begin_perf = perf_counter()
maxi2 = L[0]
for x in L[1:]:
if x > maxi2:
maxi2 = x
print("%.3fs" % (perf_counter() - begin_perf))
print(maxi1 == maxi2)
|
3.834s
4.192s
True
Dans le deuxième cas (à partir de la ligne 18), les comparaisons commencent à l’indice 1 au lieu de l’indice 0 puisque le maximum initial vaut L[0], d’où la création du slice L[1:] (micro-optimisation).
On voit que la copie réalisée par le slice a un coût de l’ordre de 10% (la proportion aurait été bien plus importante si on avait utilisé la fonction standard max car cette fonction est plus rapide qu’une boucle écrite en Python). Ce coût est faible par rapport au temps d’exécution mais il est très important par rapport au gain : on s’épargne une seule comparaison !
Si le nombre d’éléments de la liste est important et qu’il n’y a pas d’autre opération pour compenser, le coût du slice est perceptible :
from time import perf_counter
n=5*10**7
begin_perf = perf_counter()
L=list(range(n))
delta = perf_counter() - begin_perf
print(f"Temps d'exécution : {delta:.2f}s")
begin_perf = perf_counter()
L[1:]
delta = perf_counter() - begin_perf
print(f"Temps d'exécution : {delta:.2f}s")
Temps d'exécution : 0.95s
Temps d'exécution : 0.46s
L’implémentation de CPython fait que le slice L[1:] a créé 50 millions de pointeurs. Puisque la liste L crée 50 millions d’entiers et 50 millions de pointeurs, les deux temps sont cohérents (l’un est, grosso modo, le double de l’autre).
Coût non négligeable¶
Voyons une autre situation moins favorable. On se donne une liste L d’entiers et on cherche la première détection de doublon dans la liste. Par exemple, si L est la liste de contenu :
5 3 4 2 4 8 3 7 6
alors le premier doublon que l’on découvrira est 4 (qui est en 3e et 5e position). Codons ce problème de manière naïve en cherchant le premier entier de la liste que l’on a déjà rencontré si on parcourt la liste de la gauche vers la droite. Quand on est à l’indice i; les entiers déjà rencontrés forment le slice L[:i]. D’où le code
L= [5, 3, 4, 2, 4, 8, 3, 7, 6]
doublon = None
for i in range(len(L)):
x = L[i]
if x in L[:i]:
doublon = x
break
print(doublon)
4
S’il n’y a pas de doublon alors le code affiche None. On voit qu’à chaque étape de la boucle, un slice de plus en plus grand est créé et si la liste L est longue, le coût ne sera pas négligeable.
Plutôt que d’utiliser un slice, on pourrait rechercher la présence de x en utilisant la méthode index et qui peut faire une recherche d’indice d’élément dans une plage donnée. D’où le code alternatif suivant :
L = [5, 3, 4, 2, 4, 8, 3, 7, 6]
doublon = None
for i in range(len(L)):
x = L[i]
if L.index(x, 0, i + 1) < i:
doublon = x
break
print(doublon)
4
Comparons les deux codes sur une liste de 50000 entiers sans doublons. La seule différence avec les codes ci-dessus est que pour diminuer les coûts des appels L[i], on utilisera la méthode enumerate. D’où le code :
from time import perf_counter
N=50*10**3
L=list(range(N))
# ------------- Sans slices --------------
begin_perf = perf_counter()
doublon = None
for i, x in enumerate(L):
if L.index(x, 0, i+1)<i:
doublon = x
break
delta = perf_counter() - begin_perf
print(f"Sans slices : {delta:.2f}s")
# ------------- Avec slices --------------
begin_perf = perf_counter()
doublon = None
for i, x in enumerate(L):
if x in L[:i]:
doublon = x
break
delta = perf_counter() - begin_perf
print(f"Avec slices : {delta:.2f}s")
Sans slices : 10.61s
Avec slices : 13.91s
Cette fois, on voit que le surcoût n’est pas négligeable, il vaut environ 30% alors que les algorithmes sont strictement identiques.
Les remarques ci-dessus ont pour origine cette discussion.
Coût quadratique¶
Si un slice est placé dans une boucle la complexité peut devenir quadratique au lieu de rester linéaire. Considérons le code suivant :
N = 5 * 1000
L = list(range(N))
for i in range(N):
L = L[1:]
A chaque tour de boucle for, l’implémentation de Python créé autant de références qu’il y a d’éléments dans L donc au total sont créées \(\mathtt{O(N^2)}\) références.
Si on mesure le temps d’exécution :
from time import perf_counter
begin_perf = perf_counter()
N = 5 * 1000
L = list(range(N))
for i in range(N - 1):
L = L[1:]
delta = perf_counter() - begin_perf
print(f"Temps d'exécution : {delta:.2f}s")
il affiche un joli :
1 | Temps d'exécution : 0.03s
|
on se demande comment les développeurs Python ont réussi à faire en sorte que l’interpréteur crée 10 millions de pointeurs en 30 ms. Toutefois, effet quadratique oblige, si on multiplie par 10 la taille de la liste initiale, le temps d’exécution est multiplié par \(\mathtt{10^2=100}\) :
from time import perf_counter
begin_perf = perf_counter()
N = 50 * 1000
L = list(range(N))
for i in range(N - 1):
L = L[1:]
delta = perf_counter() - begin_perf
print(f"Temps d'exécution : {delta:.2f}s")
Temps d'exécution : 4.08s
Cas de range¶
Noter qu’un slice de range ne semble rien coûter :
from time import perf_counter
n=10**10
r=range(n)
begin_perf = perf_counter()
r[1:]
delta = perf_counter() - begin_perf
print(f"Temps d'exécution : {delta:.2f}s")
Temps d'exécution : 0.00s
La méthode indices¶
La méthode indices étant assez délicate à décrire, on va d’abord l’illustrer par le code ci-dessous :
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
N= len(alpha)
## Exemple 1
s = slice(12, 30, 2)
print(alpha[s])
begin, end, step = s.indices(N)
print(''.join([alpha[i] for i in range(begin, end, step)]))
print(begin, end, step)
print('----------------------------------')
## Exemple 2
s = slice(12, -30, -1)
print(alpha[s])
begin, end, step = s.indices(N)
print(''.join([alpha[i] for i in range(begin, end, step)]))
print(begin, end, step)
MOQSUWY
MOQSUWY
12 26 2
----------------------------------
MLKJIHGFEDCBA
MLKJIHGFEDCBA
12 -1 -1
La méthode indices
- s’applique à un objet de type slice (cf. lignes 5 et 8 et aussi lignes 15 et 18), disons
s; - prend un paramètre, disons
N, qui représente une longueur de séquence (ci-dessus, \(N=26\) nombre de lettres de l’alphabet) ; - renvoie trois indices
a,betctels querange(a, b, c)corresponde aux indices des éléments d’une séquence de longueurNà laquelle le slicesserait appliqué.
Par exemple, dans le code ci-dessus, si s = slice(12, -30, -1) alors s.indices(26) est le triplet \((12, -1, -1)\) : en effet, range(12, -1, -1) contient exactement les indices des éléments du slice s appliqué à une séquence de longueur 26 telle que la chaîne des lettres de l’alphabet.
Attention, contrairement à ce que l’on pourrait penser dans un premier temps (et qu’on lit parfois), slice.indices(N) ne renvoie pas des indices de slice qui appliqués à un objet (disons O), de longueur N, coïncideraient avec le slice initial appliqué à O. Par exemple :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
N= len(alpha)
## Exemple 1
s = slice(12, 30, 2)
begin, end, step = s.indices(N)
print(alpha[begin:end:step])
print(alpha[s])
print('----------------------------------')
## Exemple 2
s = slice(12, -30, -1)
begin, end, step = s.indices(N)
print(alpha[begin:end:step])
print(alpha[s])
|
18 19 20 21 22 | MOQSUWY
MOQSUWY
----------------------------------
MLKJIHGFEDCBA
|
- Lignes 7-9 et 18-19 : dans le premier exemple, il se trouve que
s.indicesrenvoie effectivement des indices valables pour un slice. - Lignes 15-17 et 21-22 : cependant, ce n’est pas le cas dans le 2e exemple puisque le slice renvoyé en appliquant à
alphales indices de retour de la méthodesequenceest vide (ligne 21) alors que le slice initial n’est pas vide (ligne 22).
Lien entre les slices et la fonction range¶
Observons le code suivant :
1 2 3 4 5 6 7 8 9 10 | s = [65, 31, 9, 32, 81, 82, 46, 12]
i = 2
j = 6
t = s[i:j]
u = [s[k] for k in range(i, j)]
print(t)
print(u)
|
11 12 | [9, 32, 81, 82]
[9, 32, 81, 82]
|
- Lignes 6 et 7 : noter l’analogie entre
s[i:j]etrange(i, j).
Plus généralement, si s est une séquence de longueur \(n\) et si i et j sont deux indices :
- soit tous les deux positifs ou nuls,
- soit tous les deux strictement négatifs,
- éventuellement invalides pour
s,
alors on a l’égalité :
list(s[i:j]) == [s[m] for m in range(i, j) if m in range(-len(s),len(s))]
et même
list(s[i:j:k]) == [s[m] for m in range(i, j, k) if m in range(-len(s),len(s))]
En fait, on dispose de bien mieux que cela : la méthode slices.indices nous fournit justement la liste de tous les indices d’une liste L extraits par le slice L[i:j:k], autrement dit, l’égalité suivante est vraie sans aucune restriction, y compris si des indices sont implicites :
L[i:j:k] == [L[m] for m in range(*slice(i, j, k).indices(len(L)))]
Que les indices i, j ou k soient implicites signifie qu’à gauche de la comparaison ==, on laisse vide l’emplacement pour i, j ou k et qu’à droite, on remplace l’indice implicite par None.
Testons cette identité sur quelques tests aléatoires, comprenant des indices implicites :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | from random import randrange
N=20
L=[randrange(10,50) for _ in range(N)]
m=5
M=list(range(-2*N, 2*N))+[None]*m
ntest=25
for _ in range(ntest):
i, j, k=[M[randrange(4*N+m)] for _ in range(3)]
if k==0:
continue
ii = i if i is not None else ''
jj = j if j is not None else ''
kk = ":" +str(k) if k is not None else ''
expr='L[%s:%s%s]' %(ii,jj,kk)
Lijk=eval(expr)
OK=(Lijk==[L[m] for m in range(*slice(i, j, k).indices(len(L)))])
if not OK:
break
if OK:
print("%s succès/%s tests" %(ntest, ntest))
else:
print("L =", L)
print("%s : ECHEC !" %expr)
|
- Ligne 5 : La liste
Moù les indicesi,jetkvont être choisis.Noneest présentmfois dans la liste. La listeMest de longueur4N+m. - Ligne 9 : le pas
kne peut pas être nul. - Ligne 15 : j’utilise la fonction
evalpour gérer facilement le cas des indices implicites.
Le code affiche :
25 succès/25 tests
Slices itérateurs¶
Jusqu’à présent, les slices utilisés sont des séquences telles que des listes ou des chaînes. Ces slices sont des itérables mais ne sont pas des itérateurs. Le cas d’un slice sur un range est analogue à celui des listes puisque le retour de range n’est pas non plus un itérateur ; ainsi, des slices de range sont encore de type range :
r = range(10, 20)
s = r[3::2]
print(type(s))
print(list(s))
<class 'range'>
[13, 15, 17, 19]
Toutefois, le module standard itertools permet de créer des slices qui ne seront pas des séquences mais plutôt des itérateurs. Pour créer de tels itérateurs, utiliser la fonction islice (écrite avec un seul s et qui abrège Iterator slice) :
1 2 3 4 5 6 7 | from itertools import islice
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
alpha_iter = islice(alpha, 5, 22, 4)
print(alpha_iter)
print(list(alpha_iter))
print(list(alpha[5:22:4]))
|
8 9 10 | <itertools.islice object at 0xb716102c>
['F', 'J', 'N', 'R', 'V']
['F', 'J', 'N', 'R', 'V']
|
- Lignes 4 et 8 :
alpha_iterest un itérateur, pas une chaîne. - Lignes 6-7 et 9-10 :
alpha_iterse comporte comme le slicealpha[5:22:4]sauf qu’il se contente d’itérer sur les éléments sans les stocker.
Les indices de l’itérateur sont les arguments donnés à la fonction islice. Les raccourcis de slices consistant à omettre les indices se traduisent pour islice par des arguments valant None. Par exemple, l’équivalent itérateur du slice s[2::-3] est islice(s, 2, None, -3). S’il n’y a que deux indices donnés en arguments, le troisième est considéré comme valant 1 ; par exemple, l’équivalent itérateur du slice s[2:5:] est islice(s, 2, 5) qui est équivalent à islice(s, 2, 5, 1) :
from itertools import islice
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
alpha_iter = islice(alpha, 3, 10)
print(list(alpha_iter))
print(list(islice(alpha, 3, 10, 1)))
['D', 'E', 'F', 'G', 'H', 'I', 'J']
['D', 'E', 'F', 'G', 'H', 'I', 'J']
Limitations à l’utilisation¶
Une limitation cependant de la fonction islice : aucun des 3 arguments représentant les indices ne peut être négatif, cf. lignes 3 et 7 dans le code ci-dessous :
1 2 3 4 5 6 7 8 9 10 11 | >>> from itertools import islice
>>> alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
>>> alpha_iter = islice(alpha, 3, 10, -1)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: Step for islice() must be a positive integer or None.
>>> alpha_iter = islice(alpha, -10, 20, 2)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: Indices for islice() must be None or an integer: 0 <= x <= sys.maxsize.
>>>
|
Cette limitation est compréhensible dans la mesure où islice travaille avec un itérateur donc, à un moment donné de l’exécution, il n’y a pas de « fin » à partir de la quelle on pourrait reculer.
D’autre part, curieusement, un objet de type islice ne conserve pas de trace des indices de slice passés en arguments et qui sont nommés habituellement start, stop et step (cf. tout retour de la fonction range) :
from itertools import islice
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
alpha_iter = islice(alpha, 3, 10, 2)
print(alpha_iter.start)
print(alpha_iter.start)
AttributeError: 'itertools.islice' object has no attribute 'start'
De même, les arguments d’indices de islice ne peuvent pas être nommés (alors que c’est possible d’ailleurs pour la fonction range) :
from itertools import islice
alpha = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
alpha_iter = islice(alpha, start=3, stop=10, step=2)
alpha_iter = islice(alpha, start=3, stop=10, step=2)
TypeError: islice() does not take keyword arguments
Limitations à l’exécution¶
Malgré les apparences, islice ne présente aucune efficacité particulière pour parcourir une tranche de liste. En effet, islice va itérer sur la totalité de la liste. L’exemple ci-dessous le montre de manière caricaturale :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | om itertools import islice
from time import perf_counter
from random import randrange
def maketest(n):
return [randrange(1,10) for _ in range(10)]*(n//10)
n=80*10**6
c=maketest(n)
print("************ islice ************")
begin_perf=perf_counter()
s1=sum(islice(c, n-2, None))
print("%.3fs" %(perf_counter()-begin_perf))
print("************ slice ************")
begin_perf=perf_counter()
s2=sum(c[n-2:])
print("%.3fs" %(perf_counter()-begin_perf))
print("************************")
print(s1, s2)
|
28 29 30 31 32 33 | ************ islice ************
0.195s
************ slice ************
0.000s
************************
10 10
|
- ligne 9 :
cest une énorme liste de 80 millions d’entiers - ligne 22 : on construit un slice des deux derniers éléments de
cet on en fait la somme. - ligne 31 : l’exécution est instantannée
- ligne 15 : on ne cherche à faire la somme que des deux derniers éléments de
c, ceux aux indicesn-2etn-1. - ligne 29 : l’exécution est loin d’être instantanée.
En réalité, il ne semble pas qu’il soit possible de parcourir une portion contiguë de séquence de manière efficace autrement qu’avec un slice (qui néanmoins effectue des copies de références).