L’efficacité de Numba sur le tri par sélection¶

Soit un code Python d’un simple tri par sélection :

def selection(L):
    n=len(L)
    for i in range(n-1):
        jMin=i
        mini=L[i]
        for j in range(i+1, n):
            if L[j] < mini:
                jMin=j
                mini=L[j]
        if mini!=L[i]:
            L[i], L[jMin]= L[jMin], L[i]

L = [19, 16, 18, 14, 18, 17, 17, 18, 14, 15]
print(L)
selection(L)
print(L)

qui affiche :

[19, 16, 18, 14, 18, 17, 17, 18, 14, 15]
[14, 14, 15, 16, 17, 17, 18, 18, 18, 19]

Testons son temps d’exécution sur une liste de 20000 entiers :

from time import perf_counter
from random import randrange

def selection(L):
    n=len(L)
    for i in range(n-1):
        jMin=i
        mini=L[i]
        for j in range(i+1, n):
            if L[j] < mini:
                jMin=j
                mini=L[j]
        if mini!=L[i]:
            L[i], L[jMin]= L[jMin], L[i]

N=20000
L=[randrange(10**6) for _ in range(N)]

print("Sorting ...")

begin_perf = perf_counter()

selection(L)

delta_py = perf_counter() - begin_perf

print(f"Python : {delta_py:.2f}s")

qui affiche

Sorting ...
Python : 7.65s

Maintenant, dans un autre fichier, on va soumettre le même test au package Numba (qui doit être disponible sur votre installation). Le nouveau code est :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

from time import perf_counter
from random import randrange
from numba import njit
import numpy as np

@njit
def selection_nb(L):
    n=len(L)
    for i in range(n-1):
        jMin=i
        mini=L[i]
        for j in range(i+1, n):
            if L[j] < mini:
                jMin=j
                mini=L[j]
        if mini!=L[i]:
            L[i], L[jMin]= L[jMin], L[i]

N=20000
L=[randrange(10**6) for _ in range(N)]
M=np.array(L, dtype=np.int64)
print("Sorting ...")

# warmup
selection_nb(np.array([42], dtype=np.int64))

begin_perf = perf_counter()

selection_nb(M)

delta = perf_counter() - begin_perf

print(f"Numba : {delta:.2f}s")

Voici les points communs entre les deux codes :

• le corps de la fonction selection reste totalement inchangé (lignes 7-17)
• on fait un appel à la fonction de la même façon (ligne 29).

Voici les différences :

• on doit importer du module Numba le nom njit (ligne 3)
• la fonction selection est décorée par le décorateur njit (ligne 6)
• on doit importer le module Numpy (ligne 4)
• la liste L donnée dans le test initial doit être convertie en un tableau Numpy (ligne 21).

Pour comprendre ce qui suit, vous n’avez pas besoin de savoir ce qu’est un décorateur (cf. ligne 6), il vous suffit d’admettre qu’il faut l’écrire au-dessus du nom de la fonction avec la syntaxe indiquée pour qu’elle soit exécutée en mode nopython.

La conversion de la liste Python en un tableau Numpy est un point essentiel (ligne 21).

Et quand on teste ce nouveau code, il affiche un joli :

Sorting ...
Numba : 0.21s

On voit donc que le code Numba traite le même problème en étant 36 fois plus rapide. On est très proche des performances du C++ : le même code mais récrit en C++ demande un temps de 0.18s.

Numba ou Numpy ?¶

On pourrait se demander si dans le cas du tri par sélection l’amélioration de performance ne serait pas due à l’utilisation de Numpy. Il n’est est rien. Si on exécute la fonction selection sans recours à Numba, le code est plus lent que du code Python pur :

from time import perf_counter
from random import randrange
import numpy as np

def selection_np(L):
    n=len(L)
    for i in range(n-1):
        jMin=i
        mini=L[i]
        for j in range(i+1, n):
            if L[j] < mini:
                jMin=j
                mini=L[j]
        if mini!=L[i]:
            L[i], L[jMin]= L[jMin], L[i]

N=20000
L=[randrange(10**6) for _ in range(N)]
M=np.array(L, dtype=np.int64)
print("Sorting ...")


begin_perf = perf_counter()

selection_np(M)

delta = perf_counter() - begin_perf

print(f"Numpy : {delta:.2f}s")

Sorting ...
Numpy : 27.54s

Rappelons que le temps en Python pur était de l’ordre de 7.65s donc le code est devenu plus de trois fois plus lent. Deux conclusions :

• Numpy ne rend pas votre code Python plus rapide ;
• c’est l’association de Numpy et Numba qui produit un code très efficace.

Problèmes de types ou de non-reconnaissance¶

Si vous vous décidez à utiliser fréquemment Numba, vous serez souvent confronté à des problèmes de typage. Ci-dessous quelques exemples variés.

Voici un problème dû à un typage hybride :

import numpy as np
from numba import njit

@njit
def f(t,x):
    t[0]=x

wedges = np.array([(3.14, 1), (2.71, 4)], dtype='float32,int32')
wedge=(0.47, 42)
f(wedges, wedge)

qui affiche (sortie tronquée) :

Traceback (most recent call last):

...

No implementation of function Function(<built-in function setitem>)
found for signature:

 >>> setitem(unaligned array(Record(f0[type=float32;offset=0],
 f1[type=int32;offset=4];8;False), 1d, C), Literal[int](0), Tuple(float64, int64))

There are 10 candidate implementations:

...

Le code suivant ne reconnait pas la fonction Python sum :

from numba import njit
import numpy as np

@njit
def f(L):
    s = sum(L)
    return s

L=np.array([5])
f(L)

Traceback (most recent call last):

...

Untyped global name 'sum': cannot determine Numba type
of <class 'builtin_function_or_method'>

Le code suivant ne reconnait pas la fonction Python str :

from numba import njit
import numpy as np

@njit
def f(L):
    n=L[0]
    s = str(n)
    return s

L=np.array([5])
f(L)

Traceback (most recent call last):

...

No implementation of function Function(<class 'str'>)
found for signature:

...

Le code suivant est rejeté car le type de H n’est pas connu :

from numba import njit
import numpy as np

@njit
def f(L):
    n=len(L)
    H=[]

f(np.array([42]))

from numba import jit

@jit
def nbsum2(n):
    s=0
    for i in range(n+1):
        s+=i*i

    return s

for n in [10**6, 5*10**6]:
    s=nbsum2(n)
    S=sum(i*i for i in range(n+1))
    print(f"n = {n} : {s==S}")

n = 1000000 : True
n = 5000000 : False

Numba appliqué au produit matriciel¶

Le produit matriciel est une situation typique où Numba peut montrer toute son efficacité : l’opération comprend trois boucles imbriquées, et lit des tableaux statiques de données numériques homogènes.

Dans ce qui suit, on va utiliser une matrice A de taille 1000 x 1000, à coefficients aléatoires parmi 0 ou 1 et on va tester le temps d’exécution du produit \(\mathtt{A\times A}\).

from time import perf_counter
from random import randrange

def product_direct(A, B):
    n, p=len(A), len(A[0])
    q=len(B[0])

    P=[[0]*q for _ in range(n)]
    for i in range(n):
        for j in range(q):
            for k in range(p):
                P[i][j]+=A[i][k]*B[k][j]
    return P

def build_matrix(n):
    return [[randrange(2) for _ in range(n)] for _ in range(n)]

n=1000
A=build_matrix(n)

begin_perf = perf_counter()

P=product_direct(A, A)

delta = perf_counter() - begin_perf

print(f"Python pur : {delta :.2f}s")

Python pur : 133.11s

from time import perf_counter
from random import randrange
import numpy as np

def product_np(A, B):
    return A@B

def build_matrix(n):
    return [[randrange(2) for _ in range(n)] for _ in range(n)]

n=1000

A=build_matrix(n)

begin_perf = perf_counter()

#  ---- Début de code à exécuter ----
Anp=np.matrix(A)
prod_np=product_np(Anp, Anp)
#  ---- Fin de code à exécuter ----

delta_np = perf_counter() - begin_perf

print(f"Numpy : {delta_np:.2f}s")

Numpy : 1.80s

from time import perf_counter
from random import randrange
import numpy as np
from numba import njit
import numpy as np

@njit
def product_nb(A, B):
    n, p=A.shape
    p, q=B.shape

    P=np.zeros((n,q), dtype=np.int64)
    for i in range(n):
        for j in range(q):
            for k in range(p):
                P[i,j]+=A[i,k]*B[k,j]
    return P

def build_matrix(n):
    return [[randrange(2) for _ in range(n)] for _ in range(n)]

n=1000
A=build_matrix(n)

# warmup
B=np.matrix([[0, 1], [0, 0]], dtype=np.int64)
product_nb(B, B)

begin_perf = perf_counter()

%timeit -r10 Anp=np.matrix(A, dtype=np.int64);P=product_nb(Anp, Anp)

1.6 s ± 85.6 ms per loop (mean ± std. dev. of 10 runs, 1 loop each)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

from time import perf_counter
from random import randrange
import numpy as np
from numba import njit,int64
import numpy as np



@njit
def product_nb(A):
    n, _=A.shape

    P=np.zeros((n,n), dtype=np.int64)
    col=np.empty(n, dtype=np.int64)
    for j in range(n):
        for k in range(n):
            col[k]=A[k,j]
        for i in range(n):
            for k in range(n):
                P[i,j]+=A[i,k]*col[k]
    return P

def product_np(A):
    return A@A

def build_matrix(n):
    return [[randrange(2) for _ in range(n)] for _ in range(n)]

n=1000
A=build_matrix(n)


Anp=np.matrix(A)

# =============================================



begin_perf = perf_counter()

#  ---- Début de code à exécuter ----
Anp=np.matrix(A)
prod_np=product_np(Anp)
#  ---- Fin de code à exécuter ----

delta_np = perf_counter() - begin_perf

print(f"Numpy : {delta_np:.2f}s")


# =============================================

# warmup
B=np.matrix([[0, 1],
        [1, 0]])
product_nb(B)


begin_perf = perf_counter()

#  ---- Début de code à exécuter ----
Anp=np.matrix(A)
prod_nb=product_nb(Anp)
#  ---- Fin de code à exécuter ----

delta_nb = perf_counter() - begin_perf

print(f"Numba : {delta_nb:.2f}s")

Numpy : 1.53s
Numba : 0.66s

Le produit matriciel et Numpy¶

Dans ce document, je vais beaucoup utiliser le produit matriciel pour effectuer des comparaisons de performances. L’algorithme est simple et est exigeant en calcul et en mémoire. Le temps de Numpy va servir de référence. Mais pour comparer des choses comparables, j’utiliserai des matrices à coefficients entiers et non pas flottants. En effet, l’implémentation de Numpy pour les tableaux en flottants est extrêmement rapide car elle s’appuie sur des bibliothèques spécialisées comme BLAS utilisant l’algorithme GEMM qui exploite les spécificités de l’architecture du processeur, en particulier les différents caches ; pour plus d’information sur cette implémentation, consulter le document (pdf) The Science of Programming Matrix Computations. En revanche, pour des nombres entiers, elle utilise l’algorithme ordinaire qui sera justement celui que j’utiliserai en Python, Numba ou C++ et donc plus approprié pour des comparaisons.

Pour être plus précis concernant l’implémentation du produit matriciel en Numpy, il est pris en charge par la fonction PyArrayMatrixProduct2 du fichier multiarraymodule.c. En regardant plus en détail l’implémentation :

#if defined(HAVE_CBLAS)
    if (PyArray_NDIM(ap1) <= 2 && PyArray_NDIM(ap2) <= 2 &&
            (NPY_DOUBLE == typenum || NPY_CDOUBLE == typenum ||
             NPY_FLOAT == typenum || NPY_CFLOAT == typenum)) {
        return cblas_matrixproduct(typenum, ap1, ap2, out);

on voit que si Numpy a été compilé avec la bibliothèque Blas (plutôt que compilé, en fait, c’est liée avec le linker) et si les matrices sont de type flottant (et pas entier) alors la bibliothèque Cblas est appelée pour réaliser le produit. En outre, le calcul peut être effectué sur plusieurs threads.

Pour savoir si Numpy a été lié a Blas, lire ce message.

Noter que d’une architecture à une autre on peut obtenir des temps très différents, même pour des produits matriciels en flottants.

Fonctions récursives¶

Il est parfaitement possible d’appeler des fonction récursives définies en mode nopython. Avec les deux bénéfices suivants :

• le plafonnement de taille de la pile des appels, de 1000 par défaut, disparaît ou devient très élévé
• l’exécution est très rapide, ce qui n’est pas le cas en Python pur.

Voici un premier exemple qui montre la disparition du plafonnement de la pile des appels : on calcule récursivement la somme des 200000 premiers entiers ;

from time import perf_counter
from numba import njit

@njit
def s(n):
    if n ==0:
        return 0
    return s(n-1)+n

#warmup
s(1)

n=200000

begin_perf = perf_counter()

print(s(n)==n*(n+1)//2)

delta = perf_counter() - begin_perf

print(f"Temps d'exécution : {delta:.2f}s")

True
Temps d'exécution : 0.00s

Je me suis limité à 200000 pour éviter l’overflow, Numba calculant avec des entiers 64 bits.

Dans l’exemple qui suit, on calcule par une récursivité inefficace un élément du tableau de Pascal. En Python pur, un tel code nécessiterait plusieurs dizaines de secondes. Ici, le code est très rapide :

from time import perf_counter
from numba import njit

@njit
def pascal(n, p):
    if 0 < p < n:
        return pascal(n-1, p)+pascal(n-1,p-1)
    return 1

#warmup
pascal(2,1)

n, p=30,14

begin_perf = perf_counter()

print(pascal(n,p))

delta = perf_counter() - begin_perf

print(f"Temps d'exécution : {delta:.2f}s")

145422675
Temps d'exécution : 0.92s

Fonction sans décorateur¶

Ce contenu n’est qu’en rapport très indirect avec Numba.

Parfois on souhaite comparer les performances d’une fonction et de la même fonction décorée par le décorateur @njit. Pour éviter de devoir écrire le code deux fois, on écrit la fonction, disons f sans décorateur et on obtient la fonction g compilée par Numba par g = njit(f), après tout, c’est exactement la définition d’un décorateur. Exemple :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

from time import perf_counter
from numba import njit

def f(n):
    s=0
    for i in range(n):
        s+=i//100
    return s

n=10**8
# ---------- Python -------------------

begin_perf = perf_counter()

s1=f(n)

delta = perf_counter() - begin_perf

print(f"f en Python : {delta:.2f}s")


# ---------- Numba -------------------

g=njit(f)
# warmup
g(1)

begin_perf = perf_counter()

s2=g(n)

delta = perf_counter() - begin_perf

print(f"f en Numba : {delta:.2f}s")

# ---------- Check -------------------

print(s1==s2)

39
40
41

f en Python : 6.86s
f en Numba : 0.03s
True

• Ligne 4 : on a écrit qu’une seule fois le code de la fonction dont les performances sont à comparer
• Lignes 24 et 30 : la fonction équivalente de f mais compilée par Numba.

La technique exposée ci-dessus est celle que l’on trouve dans le code source de Numba, par exemple :

pyfunc = array_dot_chain
cfunc = jit(nopython=True)(pyfunc)

Il existerait des alternatives plus élégantes, comme peut-être :

• disable decorators
• strip decorators

Situation de vectorisation¶

Soit le problème décrit ci-après, que l’on cherche à coder en Numpy de manière aussi efficace que possible. On part d’une tableau t d’entiers positifs, par exemple,

t = np.array([2, 4, 0, 3, 0, 1, 4])

et on veut créer un tableau u de flottants, de même longueur que t et tel que son élément à l’indice i soit obtenu de la manière suivante :

• si t[i] vaut 0 alors u[i] = 1.0

• sinon, et si on pose \(\mathtt{k= t[i]>0}\) alors

  • on génère k flottants aléatoires entre 0 et 1,
  • on en fait le produit p
  • on pose u[i] = p.

En soi, le problème n’a rien de difficile, la question est surtout de pouvoir construire u rapidement. Chaque élément de t doit être transformé par la fonction f suivante :

def f(k):
    if k:
        return np.prod(np.random.random(k))
    return 1.0

Ensuite, on peut utiliser la méthode vectorize de Numpy mais qui en fait ne vectorise rien comme expliqué dans les notes de la documentation, elle est équivalente à une boucle for en Python pur.

D’où le code suivant :

import numpy as np

def f(k):
    if k:
        return np.prod(np.random.random(k))
    return 1.0

t = np.array([2, 4, 0, 3, 0, 1, 4])
print(t)

g=np.vectorize(f)
u=g(t)

print(*("%.2f" %z for z in u))

qui affiche

[2 4 0 3 0 1 4]
0.46 0.36 1.00 0.34 1.00 0.08 0.15

La fonction g a transformé le tableau t en le tableau u comme souhaité.

Le problème est que ce code est très peu performant. Faisons un essai avec un tableau t de 10 millions d’entiers (générés par une distribution de Poisson car présenté ainsi dans le problème d’origine mais ce point est sans importance) :

from time import perf_counter
import numpy as np

def f(k):
    if k:
        return np.prod(np.random.random(k))
    return 1.0

n=10**7
t=np.random.poisson(0.8,n)
k=10
# on affiche les k premiers éléments de t
print(t[:k])

start=perf_counter()

u=np.vectorize(f)(t)

end=perf_counter()
delta=end - start

# on affiche les k premiers éléments de u
print(*("%.2f" %z for z in u[:k]))

print(f"Durée : {delta :.2f}s")

qui affiche

[0 3 0 1 0 1 1 0 0 1]
1.00 0.24 1.00 0.67 1.00 0.36 0.13 1.00 1.00 0.66
Durée : 26.76s

Naturellement, on ne souhaite pas que l’opération soit aussi longue, vu sa simplicité c’est potentiellement réalisable en C en quelques dixièmes de seconde.

Si on maîtrise bien Numpy et qu’on a une certaine pratique de la vectorisation à l’aide des fonctions builtins de Numpy, ce qui suppose de connaître le chapitre Universal functions du manuel de référence, on pourra obtenir le code suivant :

from time import perf_counter
import numpy as np

def solve(t):
    t_plus=t>0
    t_cumul_plus=np.zeros(len(t[t_plus]))
    t_cumul_plus[1:]=np.cumsum(t[t_plus])[:-1]
    t_cumul_plus=t_cumul_plus.astype(int)
    temp=np.multiply.reduceat(1+np.random.random(np.sum(t)),t_cumul_plus)
    u=np.full(n,1.0)
    u[t_plus]=temp
    return u


n=10**7
t=np.random.poisson(0.8,n)
k=10
print(t[:k])

start=perf_counter()

u=solve(t)

end=perf_counter()
delta=end - start

print(*("%.2f" %z for z in u[:k]))
print(f"Durée : {delta :.2f}s")

qui affiche

[1 0 0 0 1 1 1 1 1 1]
1.66 1.00 1.00 1.00 1.54 1.93 1.19 1.04 1.65 1.55
Durée : 0.57s

On voit que le temps a été divisé plus de 45. Le code ne contient aucune boucle for explicite ni aucune liste Python, il n’utilise que des fonctions built-in de Numpy.

Vectorisation avec Numba¶

Numba offre la possibilité de vectoriser des tableaux Numpy en décorant par le décorateur vectorize la fonction qui réalise le traitement.

Reprenons le problème traité au paragraphe précédent : on part d’une tableau t d’entiers positifs, par exemple,

t = np.array([2, 4, 0, 3, 0, 1, 4])

et on veut créer un tableau u de flottants, de même longueur que t et tel que l’élément à l’indice i soit obtenu de la manière suivante :

• si t[i] vaut 0 alors u[i] = 1.0
• sinon, et si on pose \(\mathtt{k= t[i]>0}\) alors on génère k flottants aléatoires entre 0 et 1, on en fait le produit p et on pose u[i] = p.

La fonction f qui agit sur chaque élément de t pour transformer t en u est la suivante :

def f(k):
    if k:
        return np.prod(np.random.random(k))
    return 1.0

C’est maintenant que Numba peut intervenir. Pour que f devienne une fonction de vectorisation efficace, il suffit de lui placer un décorateur :

1
2
3
4
5
6
7
8

import numpy as np
from numba import vectorize, int64, float64

@vectorize([float64(int64)])
def f(k):
    if k:
        return np.prod(np.random.random(k))
    return 1.0

Le décorateur doit être importé de Numba (ligne 2) et sa présence va entraîner la compilation de la fonction en mode nopython. La syntaxe [float64(int64)] de la ligne 4 indique que f agit sur des entiers de type int64 d’un tableau uni-dimensionnel et qui renvoie un nombre flottant de type float64 ; ces types ont été importés de Numba à ma ligne 2.

Pour vectoriser le tableau t en u, il suffit de faire un appel u = f(t). D’où le code :

from time import perf_counter
import numpy as np
from numba import vectorize, int64, float64

@vectorize([float64(int64)])
def f(k):
    if k:
        return np.prod(np.random.random(k))
    return 1.0

lam=0.8
k=10

# warmup
n=2
f(np.random.poisson(lam, n))

n=10**7
t=np.random.poisson(lam,n)
print(t[:k])

start=perf_counter()

u=f(t)

end=perf_counter()
delta=end - start

print(*("%.2f" %z for z in u[:k]))
print(f"Durée : {delta :.2f}s")

et qui affiche

[0 1 0 1 2 1 1 1 1 0]
1.00 0.79 1.00 0.63 0.01 0.85 0.40 0.57 0.73 1.00
Durée : 0.55s

La performance est très correcte et totalement comparable au code vectorisé de Numpy tout en étant beaucoup plus simple car trouver le code de Numpy nécessite un certain savoir-faire et est ici assez détourné de l’approche directe.

On peut même l’améliorer en utilisant la fonction np.rand qui est équivalente à np.random.random :

from time import perf_counter
import numpy as np
from numba import vectorize, int64, float64

@vectorize([float64(int64)])
def g(k):
    p=1.
    rand=np.random.rand
    for i in range(k):
        p*=rand()
    return p

lam=0.8
k=10

# warmup
n=2
g(np.random.poisson(lam, n))

n=10**7
t=np.random.poisson(lam,n)
print(t[:k])

start=perf_counter()

u=g(t)

end=perf_counter()
delta=end - start

print(*("%.2f" %z for z in u[:k]))
print(f"Durée : {delta :.2f}s")

et qui affiche

[1 1 0 0 1 1 1 0 1 0]
0.64 0.72 1.00 1.00 0.78 0.23 0.39 1.00 0.61 1.00
Durée : 0.19s

Par rapport au code utilisant la vectorisation Numpy définie par la méthode f.vectorize, on voit que le temps d’exécution a été divisé par 100 et sans rajouter aucune difficulté de conception.

Et naturellement c’est beaucoup plus simple que de créer une extension C de Numpy en utilisant PyUFuncType.

Il est possible de donner une instruction de parallélisation :

@vectorize([float64(int64)], target='parallel')
def f(k):
    if k:
        return np.prod(np.random.random(k))
    return 1.0

mais à l’exécution, ce code s’est avéré plus lent.

Parallélisme sur CPU¶

Numba permet la parallélisation automatique de l’exécution de certaines fonctions sur le CPU. Mais comme cette possibilité semble délicate à paramétrer, je vais me limiter à l’utilisation du parallélisme dans des boucles for avec prange et je ne vais envisager que des cas simples de parallélisme de données, ce qu’on qualifie parfois d”embarrassingly parallell.

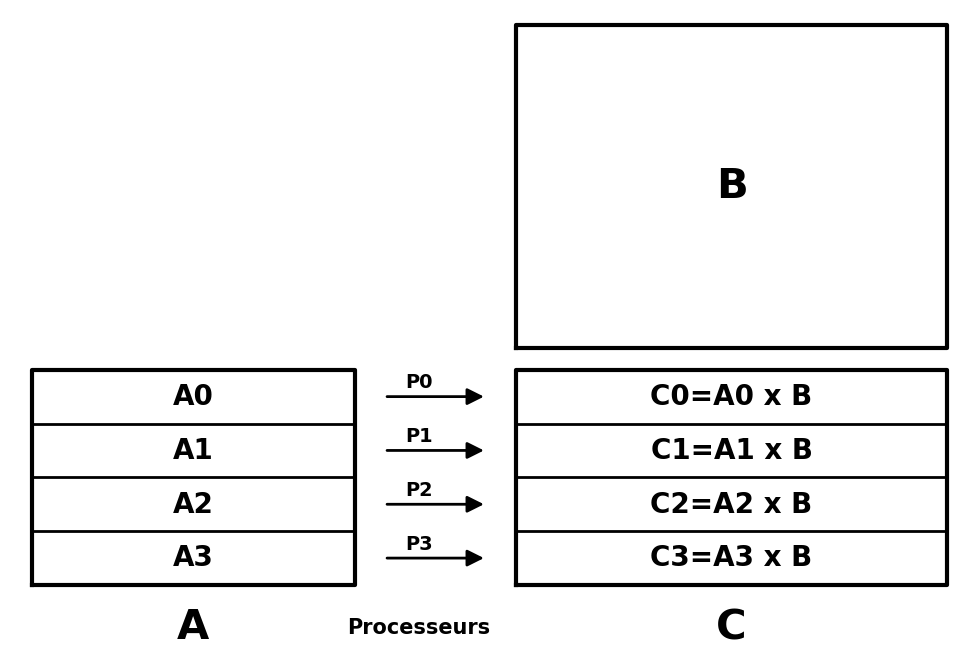
Le cas typique est celui du produit matriciel. Supposons que l’on veuille effectuer le produit \(\mathtt{A\times B=:C}\) de deux matrices de tailles respectives \(\mathtt{(n, p)}\) et \(\mathtt{(p, q)}\). Supposons que l’on dispose par exemple d’un processeur ayant 4 cœurs, qu’on assimilera à des processeurs nommés P0, P1, P2 et P3 :

Il est clair qu’on peut effectuer le calcul de \(\mathtt{C}\) en parallèle :

• on découpe la matrice \(\mathtt{A}\) en 4 sous-matrices ayant \(\mathtt{p}\) colonnes et approximativement \(\mathtt{n//4}\) lignes ;
• chaque processeur \(\mathtt{Pi}\) s’occupe de faire le produit matriciel \(\mathtt{Ai\times B=:Ci}\) ;
• la matrice \(\mathtt{C}\) est formée de l’empilement des blocs \(\mathtt{Ci}\).

Rappelons un code possible du produit matriciel de deux matrices à coefficients de type int64 :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def product(A, B):
    n, p=A.shape
    p, q=B.shape

    C=np.zeros((n,q), dtype=np.int64)
    for i in range(n):
        for j in range(q):
            for k in range(p):
                C[i,j]+=A[i,k]*B[k,j]
    return C

Sur un multi-cœur, et d’après la méthode expliquée si dessus, le parallélisme se fera ligne 6 sur la boucle portant sur les lignes d’indices i de la matrice A. En Numba, le parallélisme se traduira par la fonction décorée ci-dessous :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

import numpy as np
from numba import njit, prange

@njit(parallel=True)
def product(A, B):
    n, p=A.shape
    p, q=B.shape

    C=np.zeros((n,q), dtype=np.int64)
    for i in prange(n):
        for j in range(q):
            for k in range(p):
                C[i,j]+=A[i,k]*B[k,j]
    return C

Il y a deux modifications :

• ligne 4 : le décorateur njit qui assure la compilation en mode nopython prend un argument parallel=True ce qui signifie que la fonction va être exécutée (au moins en partie) en parallèle ;
• ligne 10 : on indique que la boucle sur i doit être exécutée en parallèle, d’où le prange(n) au lieu de range(n).

Dans le code ci-dessous, on compare les temps d’exécution par Numba, sur processeur Intel i5 ayant 4 cœurs, d’un produit matriciel en série et d’un produit matriciel en parallèle :

from time import perf_counter
import numpy as np
from numba import njit, prange
from timeit import timeit

@njit(parallel=True)
def product(A, B):
    n, p=A.shape
    p, q=B.shape

    C=np.zeros((n,q), dtype=np.int64)
    for i in prange(n):
        for j in range(q):
            for k in range(p):
                C[i,j]+=A[i,k]*B[k,j]
    return C

@njit
def product_serial(A, B):
    n, p=A.shape
    p, q=B.shape

    C=np.zeros((n,q), dtype=np.int64)
    for i in range(n):
        for j in range(q):
            for k in range(p):
                C[i,j]+=A[i,k]*B[k,j]
    return C

n=1000
A = np.random.randint(low=-1, high=2, size=(n, n), dtype=np.int64)
B = np.random.randint(low=-1, high=2, size=(n, n), dtype=np.int64)

# -------------- Numba parallel -------------------------
# warmup
I2=np.matrix([[1, 0], [0, 1]], dtype=np.int64)
product(I2, I2)

begin_perf = perf_counter()

C=product(A, B)

print("Numba parallel : %.2fs\n" %(perf_counter()-begin_perf))

# -------------- Numba serial -------------------------
# warmup
I2=np.matrix([[1, 0], [0, 1]], dtype=np.int64)
product_serial(I2, I2)

number=12
print("Numba serial : %.2fs\n" %(timeit("product_serial(A, B)",
      globals=globals(), number=number)/number))

D=product_serial(A, B)

# ---------------------------------------

# check
print(np.array_equal(C, A @ B) and np.array_equal(C, D))

qui affiche

Numba parallel : 0.34s

Numba serial : 1.33s

True

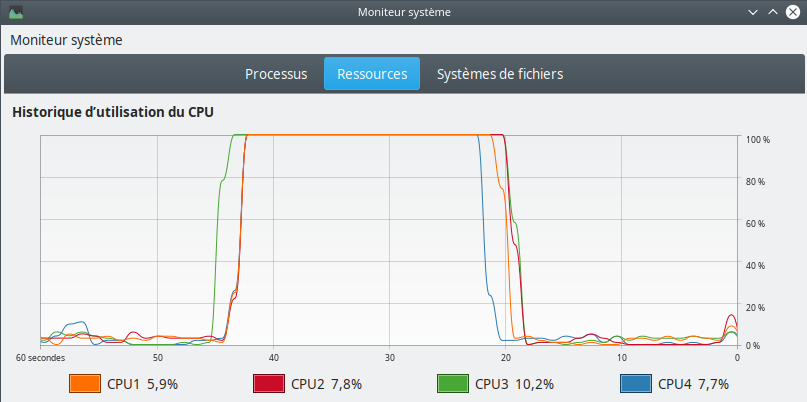
Comme les temps d’exécution du produit non parallèle étaient assez fluctuants, j’ai utilisé le module timeit pour avoir une moyenne. Par ailleurs, on observe que la version parallèle à une durée d’exécution environ 4 fois plus courte que la version normale.

Le moniteur-système sous Linux permet de visualiser l’activité des cœurs. Voici ce qu’on observe pour une exécution en parallèle pour n=3200 :