Vidéo 9 : télescopages¶
Notion de télescopage¶
Un télescopage dans une somme est une situation où une somme, une fois déployée, fait apparaître des termes qui se détruisent deux à deux (ils se télescopent).
Par exemple, calculons la somme des \(n\) premiers entiers impairs :
\(S_n=\sum_{k=1}^{n}(2k-1)\)
On remarque que
\(k^2-(k-1)^2=k^2-(k^2-2k+1)=2k-1\)
et cette remarque est à la base du télescopage. Nous allons écrire les uns en-dessous des autres les termes de la somme
\(S_n=1+3+5+\dots+(2n-3)+(2n-1)\)
en utilisant \(2k-1=k^2-(k-1)^2\). On remplace donc \(k\) par successivement \(1\), \(2\), …, \(n-1\) et \(n\) pour obtenir :
\(\begin{align}2\times 1-1 & =1^2-0^2\\2\times 2-1 & =2^2-1^2\\2\times 3-1 & =3^2-2^2\\\dots & \dots\\2\times (n-1)-1 & =(n-1)^2-(n-2)^2\\2\times n-1 & =n^2-(n-1)^2\end{align}\)
En additionnant ces égalités, on observe que :
- le membre de gauche est précisément la somme \(S_n\) ;
- dans le membre de droite, presque tous les termes entrent en collision deux à deux, puisque \(1^2\) et \(-1^2\) s’éliminent, de même que \(2^2\) et \(-2^2\), etc.
On obtient donc
\(S_n = 1^2-0^2 + 2^2-1^2 + \cdots + (n-1)^2-(n-2)^2+ n^2-(n-1)^2=n^2-0^2=n^2\)
Ainsi \(\ds\sum\limits_{i=1}^{n}(2k-1)=n^2.\) Au passage, on vérifie la justesse du résultat, par exemple, pour \(n=3\) :
\(S_3=1+3+5=9=3^2\)
Le principe du télescopage¶
Pour produire un télescopage dans le calcul d’une somme \(S_n=\ds\sum_{k=0}^{n}u_k\), il suffit de pouvoir décomposer le terme à sommer de la manière suivante
\(u_k=v_{k}-v_{k-1}\)
où \((v_k)\) est une suite inconnue. Dans l’exemple ci-dessus, on avait :
\(u_k=2k-1\quad\quad v_k=k^2\)
Si on déploie la somme \(S_n\), on se rend compte que presque tous les termes se détruisent deux à deux :
\(\begin{array}{rcl}S_n&=& u_0+u_1+u_2+\cdots+u_{n-1}+u_n\\ &=& u_0+(v_1-v_0)+(v_2-v_1)+\cdots+(v_{n-1}-v_{n-2})+(v_{n}-v_{n-1})\\ &=& u_0-v_0+v_{n}\end{array}\)
Naturellement, une somme donnée n’a, a priori, aucune raison de pouvoir se simplifier par télescopage.
1. Télescopage avec factorielles¶
On rappelle que factorielle de l’entier \(n>0\) est le nombre \(n!=1\times 2\times\cdots\times n\).
On se propose de démontrer que
\(\ds\sum_{k=1}^{n}k!\times k=(n+1)!-1\)
On posera \(S_n=\ds\sum_{k=1}^{n}k!\times k\).
- Vérifier cette formule pour \(n=4\).
- En écrivant \(k=(k+1)-1\), montrer que \(S_n=\ds\sum_{k=1}^{n}(k+1)!-\sum_{k=1}^{n}k!\).
- En déduire, en effectuant de préférence un changement d’indice, le résultat annoncé.
2. Télescopage dans le tableau de Pascal¶
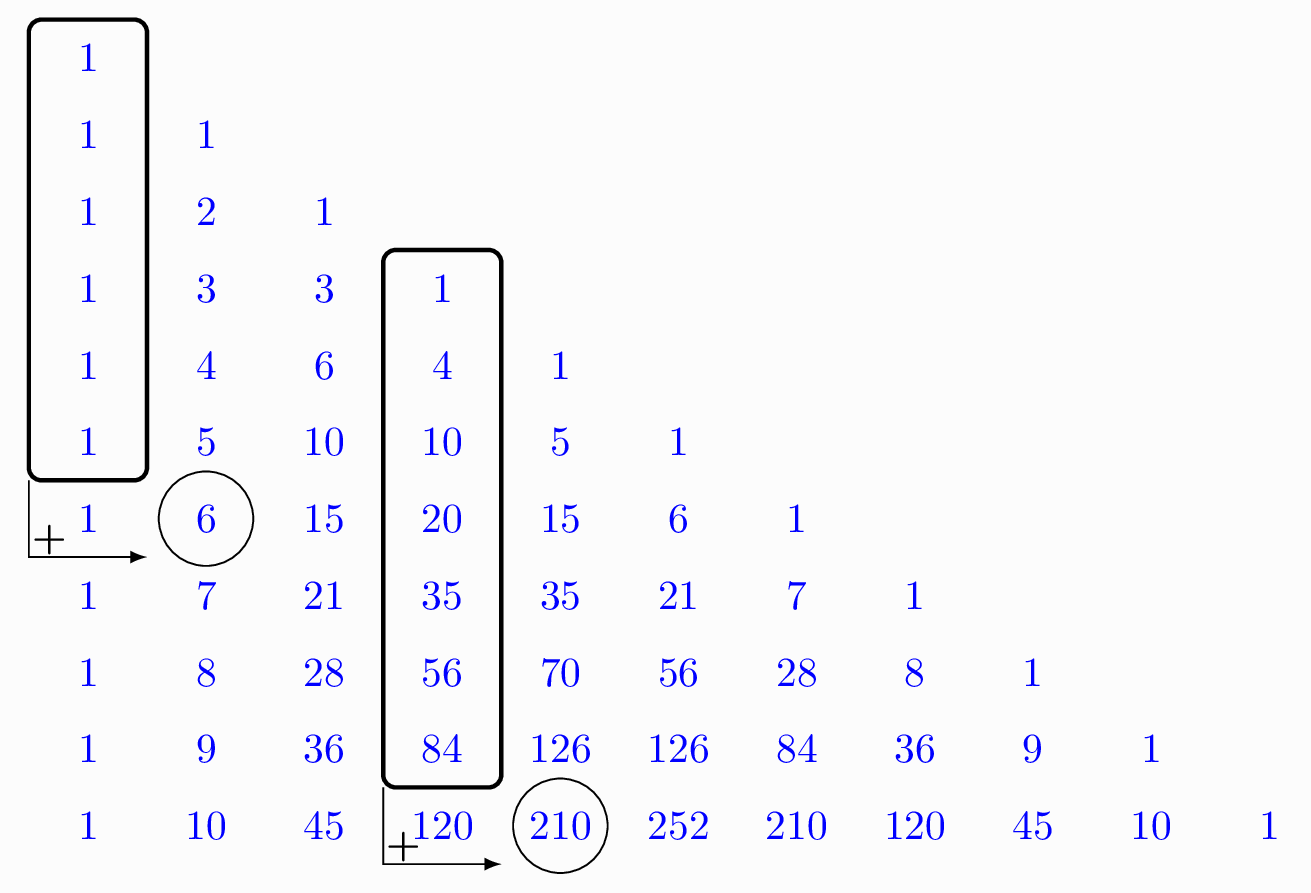
Le triangle de Pascal possède la propriété suivante : si on additionne les \(i\) premiers éléments situés dans la \(j^\text e\) colonne du triangle, on obtient le terme en \((i+1)^\text e\) position dans la \((j+1)^\text e\) colonne. Ainsi, dans la figure ci-dessous :
la somme des nombres dans chaque rectangle vaut le nombre cerclé situé en contrebas de la colonne. Ainsi,
\(1+4+10+20+35+56+84=210\)
- Traduire la propriété générale ci-dessus en utilisant le symbole sigma, l’entier \(n\), l’entier \(p\) (supposés fixés) et des coefficients binomiaux.
- Démontrer l’égalité obtenue (aide : on utilisera la formule \(\dbinom{n+1}{k+1}=\dbinom{n}{k}+\dbinom{n}{k+1}\)).