\(\newcommand{\ds}{\displaystyle}\) \(\newcommand{\Frac}{\ds\frac}\) \(\renewcommand{\r}{\mathbb{ R}}\) \(\newcommand{\C}{\mathbb{ C}}\) \(\newcommand{\n}{\mathbb{ N}}\) \(\newcommand{\z}{\mathbb{ Z}}\) \(\newcommand{\Q}{\mathbb{ Q}}\) \(\newcommand{\N}{\mathbb{ N}}\) \(\newcommand{\n}{\mathbb{ N}}\) \(\newcommand{\ol}{\overline}\) \(\newcommand{\abs}[1]{\left| \,{#1} \right|}\) \(\newcommand{\pv}{\;;\;}\) \(\newcommand{\ens}[1]{\left\{ {#1} \right\}}\) \(\newcommand{\mens}[1]{\setminus\left\{ {#1} \right\}}\) \(\newcommand{\Par}[1]{\left({#1}\right)}\)

Vidéo 42 : Triangles emboîtés¶

Triangles emboîtés¶

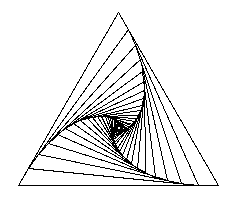
Construire un emboîtements de triangles comme dans la figure ci-dessous.

Le principe est simple : étant donné un triangle \(ABC\), on construit un autre triangle \(UVW\) tel que \(U\) soit sur le segment AB et tel que \(AU=AB/10\) et de même pour les autres côtés :

Il suffit ensuite de répéter cette construction avec le triangle \(UVW\).

On aura besoin de la transformation \(\mathtt{T(P, Q)}\) qui renvoie les coordonnées du point placé à 1/10 de PQ à partir de P :

def T(P, Q):
    return (P[0]+(Q[0]-P[0])/10, P[1]+(Q[1]-P[1])/10)

On écrira une fonction emboiter(A, B, C) qui étant donné un triangle \(\mathtt{ABC}\) comme ci-dessus dessine sous Turtle le triangle \(\mathtt{UVW}\) et renvoie la liste des coordonnées de \(\mathtt{U}\), \(\mathtt{V}\) et \(\mathtt{W}\).

Dans le dessin ci-dessus, la fonction emboiter a été appelée 25 fois. Pour des raisons esthétiques, on préférera un triangle équilatéral pour triangle initial.