Parcours indice -> élément¶

Etant donné une liste, afficher ligne par ligne chaque indice de L, suivi d’une flèche -> suivie de la valeur de L correspondant à l’indice. Par exemple, si L = [31, 12, 81, 9, 31] alors l’affichage est

0 -> 31
1 -> 12
2 -> 81
3 -> 9
4 -> 31

Valeur et indice de même parité¶

On donne une liste L d’entiers et on demande de construire un booléen memeParite qui, à partir d’un indice valide de L renvoie True si l’indice et la valeur de l’élément de L ayant cet indice sont de même parité et False sinon. Par exemple, si L

Tester avec une boucle for¶

Dans chaque question, les tests sont à effectuer au sein d’une boucle for.

1. Le code suivant montre comment, à partir d’un entier n, générer la liste formée de n-1, n et n+1 :

   n=42
   L=[n-1, n, n+1]
   

   Tester le code précédent pour les entiers n valant 42, 100, 0 et 2020. On devra obtenir l’affichage suivant :

   42 -> [41, 42, 43]
   100 -> [99, 100, 101]
   0 -> [-1, 0, 1]
   2020 -> [2019, 2020, 2021]
   

2. Le code suivant montre (et on l’admettra) comment coder un booléen qui traduit que le minimum d’une liste L d’entiers est unique :

   L=[81, 42, 87, 63, 50, 42, 42]
   miniUnique = L.count(min(L))==1
   print(miniUnique)
   

   False
   

   Appliquer le code précédent aux 5 listes suivantes :

   [42], [42, 42, 42], [81, 42, 87, 63, 50, 42, 42], [80, 42, 53, 64]

   Le code devra afficher

   [42] -> True
   [42, 42, 42] -> False
   [81, 42, 87, 63, 50, 42, 42] -> False
   [80, 42, 53, 64] -> True
   

Tests aléatoires¶

Le code suivant montre comment coder un booléen qui traduit que le minimum d’une liste L d’entiers est unique :

L=[81, 42, 87, 63, 50, 42, 42]
miniUnique = L.count(min(L))==1
print(miniUnique)

False

Générer aléatoirement 10 listes d’entiers entre 0 et 9, de longueur variable et s’assurer que le code précédent fonctionne en testant les 10 listes avec une boucle for. La sortie pourra être de la forme suivante :

[7, 9, 3, 0, 6] -> True
[2, 4, 4, 7, 3, 6, 2] -> False
[1, 7, 0] -> True
[1, 1, 3, 2, 5, 1] -> False
[6, 9, 2] -> True
[1, 9, 8, 7, 9, 2] -> True
[4, 7, 0, 7, 8, 0] -> False
[4, 9, 6] -> True
[8, 8, 1, 7] -> True
[4, 9, 5, 0, 6, 4, 8, 2] -> True

Non multiples¶

Combien y-a-t-il d’entiers entre 1 et 20000 qui ne sont ni pairs ni multiples de 5 ? Par exemple, 421 ou 2023 font partie des entiers concernés mais pas 42 ni 2025. Le nombre à trouver est 8000.

Liste cardinale¶

On dit qu’une liste d’entiers est cardinale si elle contient :

• un entier pair
• un entier multiple de 5
• un entier entre 0 et 9
• un entier strictement négatif

Par exemple, la liste [7, -1, 15, 12] est cardinale. On donne une liste d’entiers et vous devez dire si elle est cardinale ou pas.

Compter les multiples de 10¶

Calculer le nombre de multiples \(m\) de 10 tels que \(\mathtt{a\leq m < b}\) où \(\mathtt{a}\) et \(\mathtt{b}\) sont des entiers donnés. Par exemple,

a = 24 et b =  42 → 2
a = 40 et b =  42 → 1
a = 42 et b =  55 → 1
a = 40 et b =  40 → 0
a = -5 et b =  15 → 2

Décompte pair/impair¶

On donne une liste L d’entiers et on demande de calculer

• le nombre n_pair d’indices i tel que l’élément L[i] est pair
• le nombre n_impair d’indices i tel que l’élément L[i] est impair

Par exemple, si L = [31, 12, 9, 65, 81, 42] alors n_pair = 2 et n_impair = 4.

De deux en deux dans la deuxième moitié¶

On donne une liste L d’entiers, de longueur n. Si n est pair, on comprend ce qu’est la « deuxième » moitié de la liste. Si n est impair, on comprendra que la « deuxième » moitié de la liste est la plus grande de deux moitiés. Par exemple, si L = [42, 81, 12, 31, 9], la deuxième moitié de L est la liste [12, 31, 9].

On demande d’afficher un élément sur deux de la deuxième moitié de L, en commençant par son premier élément. Ci-dessous, deux exemples :

[42, 81, 12, 31, 9] -> 12 9
[42, 81, 12, 31, 9, 65] -> 31 65
[42, 81, 12, 31, 9, 65, 32, 82, 46] -> 9 32 46

Cet exercice est inspiré de Half of the half.

Impairs puis pairs¶

On donne un entier \(\mathtt{n\geq 1}\) on demande d’écrire une liste \(\mathtt{L}\) formée d’abord de tous les entiers impairs entre 1 et \(\mathtt{n}\) puis de tous les entiers pairs. Par exemple, si \(\mathtt{n=6}\), on obtiendra la liste \(\mathtt{L=[1, 3, 5, 2, 4, 6]}\) et si \(\mathtt{n=5}\), on obtiendra la liste \(\mathtt{L=[1, 3, 5, 2, 4]}\). Il est envisageable de parcourir la liste L plus qu’une fois.

Echanger côte à côte¶

Soit une liste L. Modifier L pour que

• le 1er élément et le 2ème élément soient échangés de position
• le 3ème élément et le 4ème élément soient échangés de position
• …
• et ainsi de suite jusqu’à ce que plus aucun échange ne soit possible.

Par exemple,

• si L = [31, 12, 9, 65, 81, 42] alors, après échanges, L = [12, 31, 65, 9,42, 81]
• si L = [31, 12, 9, 65, 81] alors, après échanges, L = [12, 31, 65, 9, 81]
• si L = [31] alors, après échange, L = [31]

Modifier une liste en multipliant par 10¶

On donne une liste d’entiers. Modifier cette liste pour que chaque élément \(x\) de la liste soit remplacé par \(10x\). Par exemple, si L = [31, 12, 81, 9, 65] alors, après modification, on aura L = [310, 120, 810, 90, 650].

Inverser une liste¶

Soit une liste L. Modifier L pour que

• le 1er élément et le dernier élément soient échangés de position
• le 2ème élément et l’avant-dernier élément soient échangés de position
• …
• et ainsi de suite jusqu’à ce que tous les échanges possibles soient effectués.

Par exemple,

• si L = [31, 12, 9, 65] alors, après échanges, L = [65, 9, 12, 31]
• si L = [31, 12, 81, 9, 65] alors, après échanges, L = [65, 9, 81, 12, 31]
• si L = [31] alors, après échange, L = [31]

On ne demande pas de créer une nouvelle liste, c’est simplement le contenu de L qui doit changer.

Décalages de liste¶

Les questions sont indépendantes et de difficulté croissante.

Dans ce qui suit on se donne une liste L d’entiers de longueur n.

1. Décalage à gauche. Construire une nouvelle liste M qui soit obtenue à partir de L en décalant chaque élément de L à sa gauche, sauf le premier qui est placé à l’extrémité droite de M. La liste L, elle, doit rester préservée suite à cette opération. Par exemple, si L = [9, 0, 8, 3, 0] alors alors M = [0, 8, 3, 0, 9].
2. Décalage à droite. Construire une nouvelle liste M qui soit obtenue à partir de L en décalant chaque élément à sa droite, sauf le dernier, qui est placé tout à la gauche de M. La liste L, elle, doit rester préservée suite à cette opération. Par exemple, si L = [9, 0, 8, 3, 0] alors alors M = [0, 9, 0, 8, 3].
3. Décalage à gauche en place. Modifier la liste L en décalant chaque élément à sa gauche, sauf le premier élément de L qui est placé tout à la droite de L (il n’y a pas création de nouvelle liste). Par exemple, si L = [9, 0, 8, 3, 0] alors alors L devient L = [0, 8, 3, 0, 9].
4. Décalage à droite en place. Modifier la liste L en décalant chaque élément à sa droite, sauf le dernier élément de L qui sera placé tout au début (il n’y a pas création de nouvelle liste). Par exemple, si L = [9, 0, 8, 3, 0] alors alors L devient L = [0, 9, 0, 8, 3].

Rotation de liste¶

Voici, sur un exemple, ce que l’on veut coder dans le cas général. On se donne une liste, par exemple

L = [17, 39, 61, 48, 42, 27, 75, 81, 64, 10]

et un indice k de cette liste, ici ce sera k=4 qui pointe vers l’élément 42. On souhaite effectuer une rotation des éléments dans la liste en sorte que l’élément à l’indice k soit désormais en début de liste. Donc ici, le contenu de L devra avoir changé et valoir :

L = [42, 27, 75, 81, 64, 10, 17, 39, 61, 48]

Plus généralement, les éléments à partir de l’indice k se retrouvent en début de liste et le bloc des éléments d’indices initialement inférieurs à k se retrouve, dans le même ordre, en un bloc en fin de liste. Bien noter qu’on ne demande pas de créer une nouvelle liste mais de modifier la liste initiale.

Cette manipulation de liste est l’équivalent de la fonction template standard rotate du C++.

Liste : négatif -> opposé¶

On donne une liste L d’entiers et on demande d’écrire un code qui modifie L en sorte que chaque élément \(x\) négatif de L est changé en son opposé \(-x\). Par exemple, si L est la liste [42, -9, 81, -12, -65, 0, 46] alors L doit être modifiée en la liste [42, 9, 81, 12, 65, 0, 46]

Inverser indices et valeurs dans une liste¶

On donne un entier \(\mathtt{n\geq 0}\) et on donne une liste L de \(\mathtt{n}\) entiers qui contient une fois et une seule chaque entier entre 0 et n-1. Par exemple, pour \(\mathtt{n=5}\), on pourrait avoir :

L = [1, 4, 0, 3, 2]

On demande de construire une nouvelle liste M de \(\mathtt{n}\) entiers et dont l’élément à chaque indice \(\mathtt{i}\) est l’indice de l’entier \(\mathtt{i}\) dans la liste \(\mathtt{L}\). Avec l’exemple précédent :

M = [2, 0, 4, 3, 1]

Explication : par exemple,

• M[2] = 4 car L[4] = 2.
• M[1] = 0 car L[0] = 1.

La construction de M ne doit pas modifier la liste L. On commencera par créer, avec la méthode append une liste M de \(\mathtt{n}\) entiers valant tous \(\mathtt{-1}\) puis on remplira convenablement la liste M.

Cet exercice est directement inspiré de l’exercice Choix des emplacements sur le site france-ioi.

Un, deux ou cinq¶

On considère la suite d’entiers suivante :

1, 2, 5, 10, 20, 50, 100, 200, 500, ...

où les nombres se suivent par paquet de trois en rajoutant à chaque paquet un zéro terminal au paquet précédent.

On donne un entier \(\mathtt{n\geq 0}\) et on demande de construire la liste des \(\mathtt{n}\) premiers éléments de la suite. Par exemple, si \(\mathtt{n=7}\), le code doit produire la liste :

[1, 2, 5, 10, 20, 50, 100]

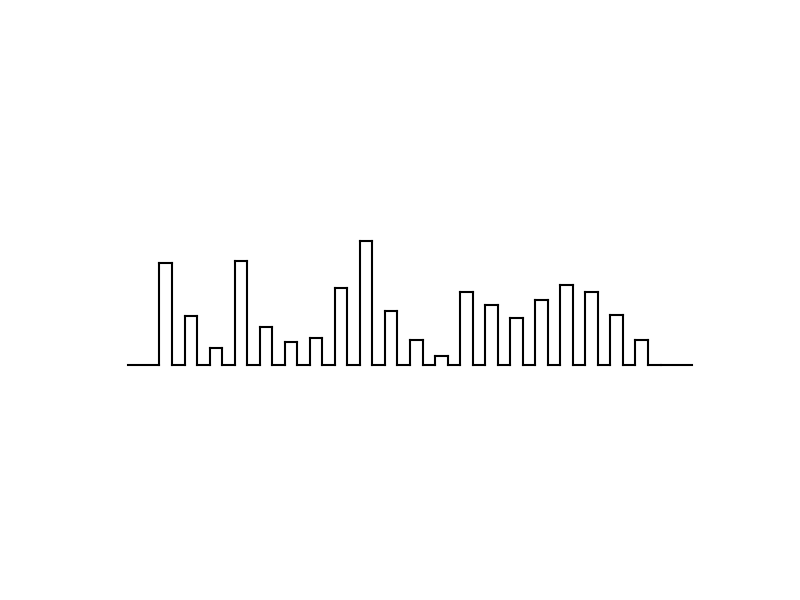
Créneaux¶

On donne une liste L de \(n\) entiers aléatoires entre 1 et 50 (vous n’avez pas à la créer). On demande de dessiner une suite de « créneaux » ayant pour hauteur les entiers de la liste L et une largeur fixe de votre choix. Les créneaux seront précédés et suivis d’une ligne horizontale. Exemple de sortie pour la liste

L = [162, 77, 26, 165, 60, 37, 43, 122, 197, 86,
     40, 14, 116, 96, 74, 103, 128, 116, 79, 40]

de longueur \(n=20\).

Disques tangents de couleurs alternées¶

On donne une liste D de \(n\) diamètres de disque et on demande de tracer ces disques, de centres alignés, chaque disque étant tangent au suivant et les couleurs de remplissage orange et bleu étant alternées. Par exemple, pour la liste

D=[47, 21, 23, 50, 37, 22, 50, 37, 55, 27,
23, 30, 41, 20, 56, 34, 5, 48, 51, 47, 27, 5, 53]

de \(n=23\) diamètres, on obtient la figure suivante :

Carrés bords à bords¶

On donne une liste L d’entiers positifs aléatoires et on demande de dessiner des carrés successifs tels que :

• les bords verticaux se touchent,
• L contient les valeurs des côtés des carrés à dessiner
• la figure dans son ensemble est symétrique par rapport à un axe horizontal.

Par exemple, si L=[19, 23, 5, 27, 99, 93, 99, 98, 89, 38, 29, 83] alors on obtient la figure suivante :

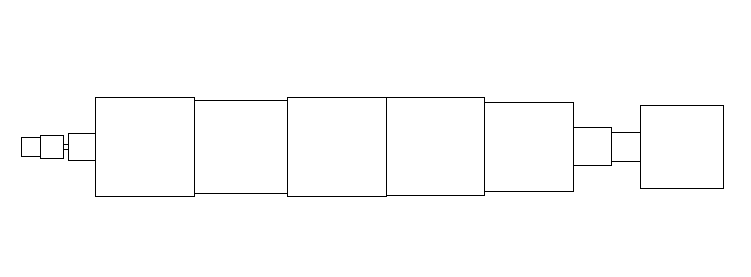
Si vous n’arrivez pas produire le motif avec ces trois contraintes, vous essayerez de produire un motif qui prend en compte seulement deux voire une seule contrainte.

Somme des multiples de 10¶

On donne une liste L d’entiers. Calculer la somme s des éléments de L qui sont des multiples de 10. Par exemple, si L = [310, 12, 8100, 90, 31] alors s = 8500.

Somme suivant les indices impairs¶

On donne une liste L d’entiers. Calculer la somme s des éléments de L dont l’indice est impair. Par exemple, si L = [31, 12, 81, 9, 31] alors s = 21.

Somme de \(n\) entiers consécutifs à partir de \(d\)¶

On vous donne deux entiers positifs d et n. On vous demande de calculer la somme des n entiers consécutifs à partir de d. Par exemple, si \(d=10\) et \(n=4\), vous devez calculer \(10+11+12+13=46\). Voici d’autres exemples :

(d, n) = (10, 1) -> 10
(d, n) = (10, 2) -> 21
(d, n) = (10, 100) -> 5950

Calcul depuis la base \(b\)¶

On donne la liste L des chiffres d’un nombre entier \(N\) écrit en base \(b\) (en commençant pas le chiffre des unités) et on demande d’afficher en base 10 la valeur de ce nombre. Par exemple, L = [4, 2, 7, 0, 5, 3] représente l’entier écrit en base 8 sous la forme 350724 et dont la valeur en base 10 est 119252.

Variations des éléments d’une liste de nombres¶

On donne une liste L d’entiers et on demande d’afficher les variations de chaque terme par rapport au précédent : si le terme augmente, le code affiche augmente sinon le code affiche diminue. Par exemple, si L=[42, 81, 12,  9, 6, 34, 30, 35, 48, 82, 32], le code affichera :

augmente
diminue
diminue
diminue
augmente
diminue
augmente
augmente
augmente
diminue

Calcul du minimum¶

On donne une liste L d’entiers. Calculer le plus petit élément mini de la liste. Par exemple, si L = [31, 9, 81, 9, 31] alors mini = 9.

Indice du minimum¶

On donne une liste d’entiers. Déterminer un indice i_mini correspondant au plus petit élément mini de la liste. Par exemple

• si L = [31, 12, 81, 9, 31] alors mini = 9 et i_mini = 3
• si L = [31, 9, 81, 9, 31] alors mini = 9 et i_mini = 1 (ou encore i_mini = 3)

En Numpy, cet indice est noté argmin.

Plus petit entier non nul (hypothèse simplificatrice)¶

On donne une liste d’entiers positifs ou nuls et telle que le premier de la liste soit non nul. On demande de déterminer le plus petit entier de la liste qui soit non nul. Exemples de fonctionnement du code :

[5, 8, 0, 9, 1, 0, 6, 4] -> 1
[5, 8, 1, 6, 4] -> 1
[5, 8, 1, -6, 4] -> -6
[-5, -8] -> -8
[-3, 0, -5, -8] -> -8
[42] -> 42
[-42] -> -42

Minimum des entiers d’indices pairs¶

On donne une liste L d’entiers. Créer et calculer une variable mini_pairs qui soit le plus petit des éléments d’indices pairs de la liste. Par exemple, si L = [81, 32, 12, 9, 10, 65, 46] alors mini_pairs = 10.

Élément de carré minimal¶

On donne une liste L d’entiers et on demande de déterminer un élément m de cette liste tel que \(\mathtt{m^2}\) soit minimal parmi les carrés de tous les éléments de L. Par exemple, si L est la liste suivante

L = [-4, 3, -4, 2, 5, -8, 6]

l’élément \(\mathtt{m=2}\) convient.

Ecart maximal de températures¶

On donne une liste L de \(n\) températures relevées au cours de \(n\geq 2\) jours consécutifs. Afficher deux températures représentant la température du jour et la température du lendemain en sorte que l’écart entre ces températures soit maximal. On pourra utiliser la fonction standard abs pour mesurer l’écart entre deux températures c’est-à-dire que abs(u-v) représente l’écart de température entre la température u et la température v. Par exemple, si L = [25, 25, 6, 14, -1, 10, 6, 10] alors le programme affichera :

25 6 -> écart maxi = 19

Alternativement début et fin¶

On donne une liste d’entiers L et on demande de réarranger les éléments de L dans une liste M en sorte qu’ils soient rangés dans l’ordre suivant :

• le premier de L
• le dernier de L
• le second de L
• l’avant dernier de L
• etc

Par exemple, la liste [5,7,9,0,2,1,3] est réarrangée en la liste [5, 3, 7, 1, 9, 2, 0].

Affichage en tas binaire (une seule boucle for)¶

Observez l’exemple suivant que l’on demande de coder dans toute sa généralité : on donne une liste L d’entiers telle que

[99, 28, 51, 76, 85, 52, 97, 97, 20, 78, 74, 34, 72, 75]

et on demande de l’afficher comme suit :

99
28 51
76 85 52 97
97 20 78 74 34 72 75

La première ligne contient le premier élément, la 2e les deux éléments suivants, la 3e contient les 4 éléments suivants et ainsi de suite, chaque ligne (sauf éventuellement la dernière) contenant deux fois plus d’éléments que la précédente.

Il est attendu de n’utiliser qu’une seule boucle for parcourant les éléments de la liste L.

Indications :

• Maintenir un compteur pour chaque ligne mémorisant le nombre d’éléments de la ligne courante qui ont été affichés.
• Maintenir une variable indiquant la longueur finale de la ligne que l’on est en train d’afficher
• Lorsqu’on arrive en fin de ligne, afficher un saut de ligne et réinitialiser le compteur

Somme des valeurs ayant même parité que l’indice¶

On donne une liste d’entiers, par exemple

L = [81, 32, 42, 82, 41, 31, 16]

On demande de calculer la somme des éléments de L qui ont même parité que l’indice où se trouve l’élément. Par exemple, ci-dessus, 81 n’intervient pas dans la somme puisque 81 qui est impair est à un indice pair, à savoir 0. De même pour 32. Mais 42 est à ajouter puisque 42 est à l’indice 2 qui est un indice pair et 42 est lui-même pair. De même pour 31 et 16. Ainsi, dans l’exemple, la somme attendue est \(\mathtt{s=42+31+16=89}\).

Le double du précédent¶

On donne une liste L d’entiers. Définir un booléen ok qui vaut True si chaque élément de la liste est le double du précédent et qui vaut False sinon. Exemple de comportements :

[10, 20, 40, 80] -> True
[12, 24, 48] -> True
[42] -> True
[0, 0, 0, 0, 0] -> True
[10, 40, 80] -> False

Nombre de carrés dans une figure (boucle)¶

On considère une figure carrée composée de disques alignés, comme ci-dessous :

Le côté du carré est formé de \(n\) disques. La figure est formée d’une succession de \(p\) carrés concentriques, tracés ici avec des couleurs différentes pour qu’ils soient bien identifiables. Dans le modèle ci-dessus, on a \(n=13\) et \(p=7\).

Notons \(p_n\) le nombre de carrés concentriques en fonction du nombre \(n\) de disques formant le côté du carré. Le dessin ci-dessus montre ainsi que \(p_{13}=7\). Vérifier que \(p_{n+2}=p_n+1\).

A partir de ce résultat, le côté \(n\) étant donné, écrire une boucle for permettant de calculer la valeur \(p_n\). Par exemple, si \(n=49\) alors on trouvera \(p_n=25\).

Entiers consécutifs en décroissant¶

On donne deux entiers \(a\) et \(b\) avec \(a\geq b\), par exemple \(a=2020\) et \(b=2000\). Afficher les entiers consécutifs depuis \(a\) jusqu’à \(b\) en ordre décroissant.

On observera qu’il y a \(a-b+1\) nombres à afficher et on pourra, par exemple, introduire dans une boucle for une variable auxiliaire \(j\) initialisée à \(a\). Mais d’autres codes sont envisageables.

Dix de plus ou de moins¶

On donne une liste L d’entiers et on demande de construire une variable booléenne OK valant True si chaque nombre de la liste vaut 10 de plus ou 10 de moins que l’élément suivant dans la liste. Sinon la variable OK vaudra False. Voici quelques exemples d’exécution attendue :

[42, 32, 22, 32, 42, 52, 62] -> True
[42, 52] -> True
[42] -> True
[42, 52, 32, 22, 32, 42, 52, 72] -> False

Liste constante¶

On donne une liste L et on demande de créer un booléen tousEgaux valant True si tous les éléments de la liste L sont égaux et False sinon. Par exemple si L = [42, 42, 42] alors tousEgaux vaudra True et si L = [42, 421, 42, 42] alors tousEgaux vaudra False.

Listes « opposées »¶

Ecrire un code qui partant deux listes d’entiers L et M crée un booléen sontOpposees valant True si les deux listes sont « opposées » et False sinon. Deux listes sont considérées comme « opposées » si elles ont le même nombre d’éléments et si, à des indices identiques, elles possèdent des éléments opposés (comme -81 et 81). Voici quelques exemples de comportements attendus :

[81, -12, 0, -81, -31] [-81, 12, 0, 81, 31] -> True
                                 [-81] [81] -> True
                              [0, 0] [0, 0] -> True
                                    [ ] [ ] -> True
                       [81, -12] [-81, -12] -> False
                     [-81, 12, 0] [81, -12] -> False

Suite croissante d’entiers consécutifs¶

Écrire un code qui à partir d’une liste \(L\) d’entiers définit une variable booléenne nommée consecutifs qui vaut True si la liste est constituée d’entiers CONSÉCUTIFS croissants et False sinon. Ci-dessous, voici quelques exemples de comportements attendus :

[81, 82, 83] -> True
[82, 81, 83, 84] -> False
[2030, 2038, 3000] -> False
[81] -> True

Suite en zig-zag¶

Une liste d’entiers, par exemple

42 81 12 98 39 48

est dite « en zig-zag » si pour chaque élément z de la liste qui n’est pas aux extrémités, son prédécesseur \(\mathtt{p}\) dans la liste et son successeur \(\mathtt{s}\) dans la liste vérifient

• ou bien \(\mathtt{z\leq p}\) et \(\mathtt{z\leq s}\)
• ou bien \(\mathtt{z\geq p}\) et \(\mathtt{z\geq s}\)

Étant donné une liste L d’entiers, écrire un booléen \(\mathtt{zigzag}\) qui vaut True si la liste L est en zigzag et False sinon. Ci-dessous, quelques exemples de comportements

[42, 81, 12, 98, 39, 48] → True
[81, 12, 98, 39, 48, 11] → True
[42] → True
[42, 81] → True
[42, 81, 82, 12] → False

Une liste de un ou deux éléments est considérée comme en zigzag.

Liste creuse¶

On dit qu’une liste formée de chiffres entre 0 et 9 est creuse s’il n’existe jamais deux chiffres voisins non nuls. Par exemple, les listes suivantes sont creuses

[4, 0, 2, 0, 5, 0, 0, 0, 6, 0, 4]
[0, 0]
[0]
[5]
[]

tandis que la liste

[4, 0, 2, 5, 0, 0, 0, 6, 0, 4]

n’est pas creuse puisque les chiffres non nuls 2 et 5 sont voisins.

Ecrire un code qui partant d’une liste de chiffres entre 0 et 9 définit une variable booléenne estCreuse indiquant si la liste L est creuse ou pas.

Liste qui patine¶

On dit qu’une liste d’entiers L patine s’il existe une position dans la liste telle que l’élément qui suit cette position et l’élément qui précède cette position ont même valeur. Par exemple, [5, 3, 6, 3, 8] est une liste qui patine puisque, autour de l’élément 6, il y a deux valeurs identiques ; en revanche, la liste [5, 3, 6, 4, 8] n’est pas une liste qui patine.

On demande d’écrire un booléen patine qui dit si oui ou non, une liste L patine.

Voici quelques exemples de comportements :

[5, 3, 6, 3, 8] → True
[5, 3, 6, 5, 8] → False
[5, 3, 5] → True
[5, 5] → False
[5] → False

Regroupement par signe¶

On donne une liste L d’entiers et on demande de construire un booléen signe qui vaut True si les deux conditions suivantes sont satisfaites :

• tous les éléments positifs ou nuls sont côte à côte
• tous les éléments négatifs ou nuls sont côte à côte

et qui vaut False sinon.

Voici quelques exemples de comportements :

[-42, -81, 31, 12, 32] → True
[-42, -81, 31, -12, 32] → False
[31, 12, 32] → True
[-42, -81] → True
[-42, -81, 31, -12, -32] → False

On pourra introduire un booléen change, initalisé à False et qui surveillera le premier moment dans le parcours de L où deux termes successifs ont des signes différents.

Égaux et côte-à-côte¶

Étant donné une liste d’entiers, par exemple

L=[81, 50, 32, 50, 42, 42, 24, 10, 10, 10, 25]

on demande de construire un entier j valant le premier indice i tel que les élements de L aux indices i et i + 1 soient égaux et si cet indice n’existe pas, j vaudra la longueur de la liste L.

Pour la liste L ci-dessus, la réponse est j=4. Pour la liste L=[31, 42, 31], la réponse est j=3 et pour la liste L=[42], la réponse est j=1.

Pour information, signalons qu’une fonction adjacent_find de la bibliothèque standard du C++ résout ce problème.

Cumul de dénivelé¶

Un randonneur effectue un parcours en montagne. On relève différentes altitudes auxquelles il passe. On demande de calculer le dénivelé total qu’il aura effectué. Par exemple, si la liste des altitudes auxquelles il est passé est

L=[1000, 1200, 1300, 800, 1000, 900]

alors le cumul de dénivelé est de

d= 200+100+500+200+100=1100.

Home Sweet Home¶

Lorsque les parents du Petit Poucet vont faire disparaître leurs enfants dans la forêt, le Petit Poucet marque comme indiqué ci-dessous tous les déplacements :

• 1 pour aller à droite
• 2 pour aller à gauche
• 3 pour aller tout droit
• 4 pour monter
• 5 pour descendre.

On vous donne la liste de ces déplacements, par exemple

[3, 2, 3, 4, 5, 1]

et on demande d’afficher la suite des déplacements que le Petit Poucet doit effectuer pour ramener sa fratrie à la maison. Avec l’exemple ci-dessus, votre code doit afficher :

2
4
5
3
1
3

Explication de la réponse : pour revenir à la maison, le Petit Poucet doit inverser tous les déplacements effectués en commençant par les derniers déplacements. Ainsi :

• le premier déplacement du Petit Poucet pour rentrer sera d’aller à gauche (code 2) car le dernier déplacement dans la forêt était d’aller à droite (code 1) ;
• le déplacement suivant du Petit Poucet pour rentrer sera de monter (code 4) car l’avant-dernier déplacement dans la forêt était de descendre (code 5) ;
• et ainsi de suite pour les 4 autres déplacements du retour.

Cet exercice est une adaptation du problème de france-ioi intitulé Visite de la mine.

Concaténer des entiers consécutifs¶

Si on écrit côte-à-côte tous les entiers entre 1 et n = 42, on obtient le très grand entier N suivant :

123456789101112131415161718192021222324252627282930313233343536373839404142

On peut vérifier que N est un entier composé de \(\mathtt{p=75}\) chiffres. Ce qui peut se calculer de la manière suivante :

• pour les entiers entre 1 et 9 : 9 chiffres
• pour les entiers entre 10 et 42 : \(\mathtt{(42-10+1)\times 2=66}\) chiffres

d’où le total de \(\mathtt{9+66=75}\) chiffres.

Plus généralement, étant donné un entier \(\mathtt{n\geq 1}\), on place côte-à-côte tous les entiers entre 1 et \(\mathtt{n}\) ce qui construit un très grand entier \(\mathtt{N}\). On demande de calculer le nombre \(\mathtt{p}\) de chiffres de \(\mathtt{N}\).

On n’utilisera pas de chaînes pour résoudre ce problème. On procédera plutôt de la manière suivante :

• on parcourt dans une boucle tous les entiers \(\mathtt{i}\) entre 1 et \(\mathtt{n}\) ;
• dans une variable k on conserve le nombre de chiffres de l’entier courant \(\mathtt{i}\) ;
• lorsque \(\mathtt{i}\) franchit une puissance de 10, on met à jour \(\mathtt{k}\) en l’augmentant de 1 puisque quand on passe une puissance de 10, les nombres ont un chiffre de plus : par exemple avant \(\mathtt{10^3}\) les nombres ont trois chiffres et à partir de \(\mathtt{10^3}\), ils en ont quatre.

Le code devra pouvoir répondre en quelques secondes pour des entiers très grands, de l’ordre de plusieurs dizaines de millions. Pour \(\mathtt{n=2020}\), on trouvera \(\mathtt{p=6973}\).

Cette famille de nombres est enregistrée dans la base de suites d’entiers OEIS.

Médiane d’une liste de nombres¶

Etant donné une liste L de nombres, on dira qu’un nombre \(\mathtt{m}\) est une médiane de L si le nombre d’éléments \(\mathtt{x}\) de la liste L qui vérifient \(\mathtt{x\leq m}\) est égal au nombre d’éléments \(\mathtt{y}\) de la liste L qui vérifient \(\mathtt{y\geq m}\). Par exemple, si L est la liste de 8 éléments suivante

L = [17, 24, 17, 22, 22, 24, 22]

alors

• le nombre \(\mathtt{m=22}\) est une médiane de L car il existe 5 éléments \(\mathtt{x}\) dans la liste qui vérifient \(\mathtt{x\leq 22}\) et il y en a autant qui vérifient \(\mathtt{x\geq 22}\) ; dans le premier cas, on trouve 17, 17, 22, 22 et 22 et dans le second, on trouve 24, 22, 22, 24 et 22, ce qui fait 5 éléments dans les deux cas ;
• le nombre \(\mathtt{m=20}\) n’est pas une médiane de la liste puisqu’il existe 2 éléments \(\mathtt{x}\) dans la liste qui vérifient \(\mathtt{x\leq 20}\) mais il en existe 5 qui vérifient \(\mathtt{x\geq 20}\).

On donne une liste de nombres L et un nombre m est on demande de calculer un booléen estMediane qui vaut True si m est une médiane de L et False sinon.

Compter les hausses et les baisses¶

On donne une liste L d’entiers, par exemple

L = [12, 15, 14, 14, 14, 10, 16, 15]

Soit i un indice de cette liste, autre que le dernier. On dit que L présente :

• une hausse à l’indice i si \(\mathtt{h=L[i+1]-L[i] \geq 0}\) et dans ce cas on dit que la valeur de la hausse est \(\mathtt{h}\)
• une baisse à l’indice i si \(\mathtt{b=L[i+1]-L[i] \leq 0}\) et dans ce cas on dit que la valeur de la baisse est \(\mathtt{-b}\).

On demande d’écrire un programme qui détermine la liste [H, B] où \(\mathtt{H}\) est la somme des hausses et \(\mathtt{B}\) est la somme des baisses de la liste L. Dans le cas de l’exemple ci-dessus, la réponse attendue est [9, 6].

Cet exercice est inspiré de l’exercice Alpiniste de la demi-finale du concours Algoréa 2018

Valeurs paires d’une liste¶

Soit une liste L d’entiers. Séparer cette liste en deux listes :

• la liste P des entiers pairs de L
• la liste I des entiers impairs de L

Par exemple, si L = [31, 12, 9, 65, 81, 42] alors P = [12, 42] et I = [31, 9, 65, 81]

Sous-liste strictement croissante¶

On donne une liste non vide d’entiers. On veut en extraire la sous-liste obtenue de la manière suivante : on part du premier élément de la liste, on la parcourt du début à la fin et on ne garde un élément que s’il est strictement supérieur au dernier choisi.

Par exemple, si la liste est

[2, 1, 2, 5, 5, 4, 6, 8, 4, 9]

la liste à construire est

[2, 5, 6, 8, 9]

Cet exercice est inspiré de l’exercice Lire ou ne pas lire, telle est la question sur France-ioi.

Trier une liste par signe¶

On donne une liste d’entiers, par exemple L=[42, -31, -42, 0, 33, 75, -12, -13, 0] et on demande de construire une liste M dont les éléments soient ceux de L mais triés suivant leurs signes : les négatifs d’abord, les éléments nuls puis les positifs. Avec la liste précédente, M sera la liste suivante :

[-31, -42, -12, -13, 0, 0, 42, 33, 75]

Il est envisageable de parcourir la liste L plusieurs fois.

Indices pairs et indices impairs¶

Soit une liste L. Séparer cette liste en deux listes :

• la liste IP des éléments de L d’indices pairs
• la liste II des éléments de L d’indices impairs

Par exemple, si L = [31, 12, 9, 65, 81, 42] alors IP = [31, 9, 81] et II = [12, 65, 42].

Subdivision régulière¶

On donne deux nombres \(\mathtt{a}\) et \(\mathtt{b}\) avec \(\mathtt{a\leq b}\) et un entier \(\mathtt{n\geq 1}\). On demande de construire la subdivision régulière \(\mathtt{S}\) d’origine \(\mathtt{a}\) et d’extrémité \(\mathtt{b}\) et de pas \(\mathtt{\ds\frac{b-a}{n}}\) c’est à dire la liste des \(\mathtt{n+1}\) éléments commençant à \(\mathtt{a}\), se terminant à \(\mathtt{b}\) et régulièrement espacés de \(\mathtt{\ds\frac{b-a}{n}}\). Par exemple, la subdivision d’origine \(\mathtt{a=4.2}\), d’extrémité \(\mathtt{b=6}\) et pour \(\mathtt{n=20}\) est la liste suivante :

[4.2, 4.29, 4.38, 4.47, 4.56, 4.65,  4.74,
4.83, 4.92, 5.01, 5.1, 5.19, 5.28, 5.37,
5.46, 5.55, 5.64, 5.73, 5.82, 5.91, 6.0]

On demande en fait de réimplémenter un comportement très proche de la fonction Numpy arange.

Pour limiter l’amplitude d’affichage de la partie décimale, on pourra utiliser la fonction round suivant l’exemple ci-dessous :

x=4.2+(6-4.2)/20*3
print(x)
print(round(x, 2))

4.470000000000001
4.47

Fonction linspace¶

On donne trois entiers a, b et n où \(\mathtt{n\geq 0}\) et on demande de créer une liste L de n nombres, tels que

• le premier élément soit a,
• le dernier soit b,
• les éléments de L soient régulièrement espacés.

Par exemple, si a=42, b=72 et n=4 alors le programme doit créer la liste

L = [42.0, 52.0, 62.0, 72.0]

(il y a un écart de 10 entre chaque nombre).

On pourra remarquer que si \(\mathtt{n\neq 1}\) alors l’écart entre deux éléments consécutifs de L est \(\mathtt{\frac{b-a}{n-1}}\) (cet écart peut être négatif). Si n=1, on conviendra que L=[a].

Voici quelques exemples du comportement du programme :

a=42, b=72, n=4
→ L = [42.0, 52.0, 62.0, 72.0]

a=2020, b=2042, n=6
→ L = [2020.0, 2024.4, 2028.8, 2033.2, 2037.6, 2042.0]

a=2042, b=2020, n=6
→ L = [2042.0, 2037.6, 2033.2, 2028.8, 2024.4, 2020.0]

a=2020, b=2042, n=0
→ L = []

a=2020, b=2042, n=1
→ L = [2020]

a=2042, b=2042, n=4
→ L = [2042.0, 2042.0, 2042.0, 2042.0]

Le comportement du programme est inspiré d’une fonction du nom de linspace disponible dans le module Numpy.

Concaténer deux listes¶

On donne deux listes L et M. Créer en utilisant la méthode append une nouvelle liste C formée des éléments de L suivis des éléments de M. Les listes L et M doivent être préservées. Par exemple, si L = [31, 12, 9] et si M = [65, 81] alors C = [31, 12, 9, 65, 81].

Somme de deux listes¶

Soient les deux listes L et M suivantes :

L = [16, 19, 11, 18]
M = [13, 16, 16, 15, 11, 10, 10]

On définit la somme S de ces deux listes comme étant la liste suivante :

S = [29, 35, 27, 33, 11, 10, 10]

Plus généralement, on donne deux listes L et M d’entiers, pas forcément de même taille, et on demande de construire une nouvelle liste S dont les termes aux indices communs soient la somme des termes de L et M ou, s’il n’y a pas d’indice commun, en gardant le terme. Suite à la construction de S, les listes L et M ne doivent pas êtres modifiées.

Intersection de deux segments¶

On donne 4 entiers \(\mathtt{a}\), \(\mathtt{b}\), \(\mathtt{c}\) et \(\mathtt{d}\) avec \(\mathtt{a< b}\) et \(\mathtt{c< d}\). Déterminer la liste L des entiers communs à range(a, b) et range(c,d). Cette liste sera écrite dans l’ordre croissant et la liste pourra, bien sûr, être vide.

Voici quelques exemples :

a = 16 b = 28
c = 11 d = 20
L = [16, 17, 18, 19]
------------------------
a = 26 b = 27
c = 21 d = 27
L = [26]
------------------------
a = 22 b = 27
c = 10 d = 18
L = []
------------------------
a = 16 b = 22
c = 17 d = 27
L = [17, 18, 19, 20, 21]
------------------------
a = 14 b = 18
c = 13 d = 21
L = [14, 15, 16, 17]

Répartition dans l’ordre¶

On veut répartir \(\mathtt{N}\) pièces de monnaie parmi \(\mathtt{p}\) individus i1, i2, …, ip. Pour cela, on procède de la manière suivante : on donne 1 pièce à i1, puis une pièce à i2, et ainsi de suite jusqu’à ip et on recommence avec i1, puis i2, etc jusqu’à épuisement des pièces.

On demande de produire une liste de p entiers contenant le nombre de pièces que va recevoir i1, i2, etc.

Par exemple, si \(\mathtt{N=42}\) et \(\mathtt{p=5}\), la distribution sera la liste suivante :

[9, 9, 8, 8, 8]

Si \(\mathtt{N=40}\) et \(\mathtt{p=5}\), la distribution sera la liste suivante :

[8, 8, 8, 8, 8]

Si \(\mathtt{N=4}\) et \(\mathtt{p=5}\), la distribution sera la liste suivante :

[1, 1, 1, 1, 0]

Minimum des entiers pairs (boucle for)¶

On donne une liste L d’entiers contenant au moins un entier pair. Ecrire un code qui calcule le plus petit des éléments pairs de la liste. Exemples de comportements :

[81, 32, 12, 9, 12, 65, 46] -> 12
[81, 65, 46] -> 46

On parcourra la liste et on pourra utiliser un drapeau qui indique si un entier pair a été rencontré ou pas.

Minimum présent une seule fois¶

On donne une liste L d’entiers. Soit mini le plus petit élément de la liste. Construire une variable miniUnique qui vaut True ou False selon que mini apparaît une seule fois dans la liste ou au contraire, plusieurs fois. Par exemple

• si L = [31, 12, 81, 9, 31] alors mini = 9 et miniUnique=True ;
• si L = [31, 9, 81, 9, 31] alors mini = 9 et miniUnique=False.

Entiers consécutifs mélangés¶

On vous donne une liste L de \(\mathtt{n}\) entiers et vous devez construire un booléen ok valant True si les éléments de L forment tous les différents entiers entre 1 et n mais placés dans le désordre. Par exemple, si L=[5, 2, 1, 4, 3] alors ok vaudra True. En revanche si L=[12, 1, 3] ou encore L=[1, 1, 3] alors ok vaudra False. Votre code doit fonctionner pour \(\mathtt{n}\) valant plusieurs millions. On pourra construire une liste auxiliaire formée de n+1 éléments et telle qu’à l’indice \(\mathtt{i>0}\) on lise le nombre d’occurrences de \(\mathtt{i}\) dans la liste \(\mathtt{L}\).

Sommer des éléments successifs d’une liste¶

Illustrons sur un exemple le problème à résoudre. On se donne un entier \(m=20\) et une liste d’entiers, par exemple

L=[5, 10, 2, 9, 3, 8, 7, 2, 4, 5, 9]

On parcourt la liste L et on fait la somme des éléments parcourus tant que la somme \(s\) vérifie \(s\leq m\). Ici, on obtient les éléments 5, 10, 2 et une somme \(s=17\). On place alors la somme \(s\) dans une liste M. Et on recommence avec la suite des éléments de L : on fait la somme des éléments parcourus tant que la somme \(s\) vérifie \(s\leq m\). Ici, on obtient les éléments 9, 3, 8, de somme 20, et on rajoute le résultat à la liste M déjà obtenue, ce qui donne M = [17, 20]. Et on poursuit jusqu’à épuisement de la liste L. Ici, on obtient M = [17, 20, 18, 9].

Plus généralement, on se donne un entier \(m\), par exemple \(m=20\) et on se donne une liste L d’entiers compris entre \(1\) et \(m\). On demande de créer une nouvelle liste M formée des sommes des éléments successifs de L et de valeur au plus \(m\).

Voici quelques de comportements pour \(m=20\) :

[7, 4, 4, 9, 8] -> [15, 17]
[7, 4, 4] -> [15]
[7, 4, 9] -> [20]
[7, 4, 10] -> [11, 10]
[7, 4, 4, 10, 10] -> [15, 20]
[17] -> [17]
[20] -> [20]

[1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1] -> [20]

[1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] -> [20, 1]

[10, 20] -> [10, 20]

[7, 4, 4, 9, 8, 9, 4, 6, 9, 9,
4, 8, 4, 7, 8, 5, 4, 4, 6, 6] -> [15, 17, 19, 18, 16, 20, 20]

Élément de rang n de la suite des entiers k répétés k fois¶

On considère la suite infinie des entiers écrits dans l’ordre croissant telle chaque entier \(k\geq 1\) est répété \(k\) fois :

1 2 2 3 3 3 4 4 4 4 5 5 5 5 5 6 6 6 6 6 6 7 7 7 7 7 7 7 etc

En examinant la suite ci-dessus, on voit, par exemple, que

• le 10e élément vaut 4
• le 16e élément vaut 6.

À partir d’un entier \(n\geq 1\), on demande de déterminer l’entier \(N\) qui se trouve en \(n\)-ème position de la suite. Ainsi, si \(n=10\) alors N=4 et si \(n=16\) alors N=6.

Formule pour la suite des entiers k répétés k fois¶

On considère la suite infinie des entiers écrits dans l’ordre croissant telle chaque entier \(k\geq 1\) est répété \(k\) fois :

1 2 2 3 3 3 4 4 4 4 5 5 5 5 5 6 6 6 6 6 6 7 7 7 7 7 7 7 etc

Vérifier pour la suite ci-dessus formée des entiers concécutifs jusqu’à 10000 que l’élément de cette suite qui arrive en \(\mathtt{n^{\text{e}}}\) position est le plus proche entier de \(\mathtt{\sqrt {2n}}\). Le proche entier d’un nombre flottant \(\mathtt{z}\) s’obtient par \(\mathtt{round(z)}\). Ce résultat est annoncé sur math-stackexchange.

Plateau le plus long¶

On donne une liste d’entiers et on recherche un entier qui est répété consécutivement dans la liste le plus grand nombre de fois (ce qui forme un « plateau »). Par exemple, la liste

[4, 8, 8, 8, 8, 7, 7, 7, 7, 7, 9, 4, 4, 4, 4, 4, 5, 5, 5]

montre un plateau de quatre 8, de cinq 7, de cinq 4 et trois 5. Donc, une réponse au problème est 7 ou 4. Attention, bien que 4 apparaisse 6 fois, il n’apparait consécutivement que suivant un plateau de longueur 5.

Si tous les nombres sont différents, il n’y a que des plateaux de longueur 1 et le programme peut renvoyer n’importe quel élément de la liste.

On pourra procéder comme suit :

• parcourir la liste avec une boucle for
• chaque fois qu’on entre dans un « plateau », on définit un compteur pour ce plateau que l’on incrémente tant qu’on reste sur le plateau
• on surveille si le compteur dépasse la taille maximale déjà atteinte, et si nécessaire, on met à jour et on mémorise le nombre dont la répétition forme le plateau.

Cet exercice provient des demi-finales 2017 du concours Algoréa.

Dupliquer une liste sur une certaine longueur¶

On donne une liste t d’entiers, par exemple

t = [12, 81, 31]

et un entier \(\mathtt{n\geq 0}\), par exemple \(\mathtt{n=8}\) et on demande de créer une liste \(\mathtt{L}\), de longueur n et de contenu celui de t répété jusqu’à ce que la liste L soit complètement remplie. Avec l’exemple ci-dessus, \(\mathtt{L}\) vaudra :

L = [12, 81, 31, 12, 81, 31, 12, 81]

Cet exercice trouve son origine dans une discussion sur le forum Python d’OpenClassrooms.

Pics d’une liste¶

On donne une liste L d’entiers, par exemple

L = [12, 15, 11, 11, 11, 10, 12, 9, 16, 15]

Soit i un indice de cette liste, autre que le premier ou le dernier. On dit que L présente un pic en l’indice i si la valeur de L en l’indice i est strictement supérieure aux valeurs de L en les deux indices voisins. Dans le cas de l’exemple ci-dessus, L présente un pic à l’indice 6.

On demande d’écrire un programme qui calcule le nombre total de pics d’une liste L. Dans le cas de l’exemple ci-dessus,

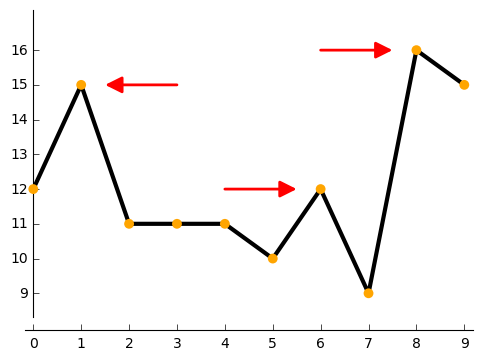
la réponse attendue est 3.

Cet exercice est inspiré de l’exercice intitulé Sommets de la demi-finale du concours Algoréa 2018

Compression de liste¶

On donne une liste \(\mathtt{L}\) d’entiers à partir de laquelle on devra générer une nouvelle liste \(\mathtt{M}\). Ainsi, si

\(\mathtt{L=[81, 81, 81, 33, 42, 42, 42, 42]}\)

alors la liste \(\mathtt{M}\) sera

\(\mathtt{M=[3, 81, 1, 33, 4, 42]}\)

Pour cela, on parcourt la liste \(\mathtt{L}\) et à chaque étape, on compte les éléments successifs identiques de \(\mathtt{L}\). Par exemple, avec la liste \(\mathtt{L}\) ci-dessus, on compte

• 3 fois de suite la valeur 81
• 1 fois la valeur 33
• 4 fois de suite la valeur 42.

La liste \(\mathtt{M}\) est alors constituée de la suite formée

• du nombre de valeurs répétées consécutives
• de la valeur répétée.

On demande d’écrire un code Python qui à partir d’une liste L construit la liste M.

Nombre de McNugget¶

On dit qu’un entier positif est un nombre de McNugget si on peut l’écrire comme une somme de multiples positifs ou nuls de 6, 9 ou 20 (cela vient du fait que les boîtes de Chicken McNuggets sont composées de 6, 9 ou 20 pièces). Par exemple, 2077 est un nombre de McNugget car \(2077 = 2\times 6+ 5\times 9+ 101\times 20\). D’un autre côté, il est clair que 25 n’est pas un nombre de NcNugget car \(25-20=5\) est trop petit et 25 n’est pas une somme de multiples de 6 ou 9.

Vérifier qu’entre 0 et 1 million, le plus grand nombre qui n’est pas un nombre de McNugget est 43. Pour cela, on créera une liste L de booléens indexée jusqu’à 1 million et telle que L[k] vaille True exactement si k est déjà identifié comme un nombre de McNugget. Pour cela, la liste sera remplie initialement que de valeurs False ; on posera L[0]=True et on parcourra la liste L et à l’indice k, on placera la valeur True si à un des indices précédents et supposés valides k-6, k-9 ou k-20, la valeur dans la liste est True (cette technique algorithmique s’appelle de la programmation dynamique).

Dessiner une spirale¶

Dessiner une ligne en forme de spirale et effectuant \(n\) tours. Le départ se fera à l’origine \((0,0)\). Pour chaque tour, on se déplacera de la même distance deux fois de suite (suivant un demi-carré) puis les deux fois suivantes la distance sera plus grande d’une distance constante esp connue au départ (et la trajectoire sera encore un demi carré). Chaque cycle consiste à se déplacer suivant le schéma droite - haut - gauche - bas. Au départ, on choisira la première longueur valant esp défini plus haut.

Le dessin ci-dessous a été construit pour n=5 et esp=10 (et le centre de la spirale est le point (0,0)) :

Tables de Plouffe¶

On va représenter une table de multiplication par des cordes sur un cercle ce qui va produire un motif surprenant, par exemple :

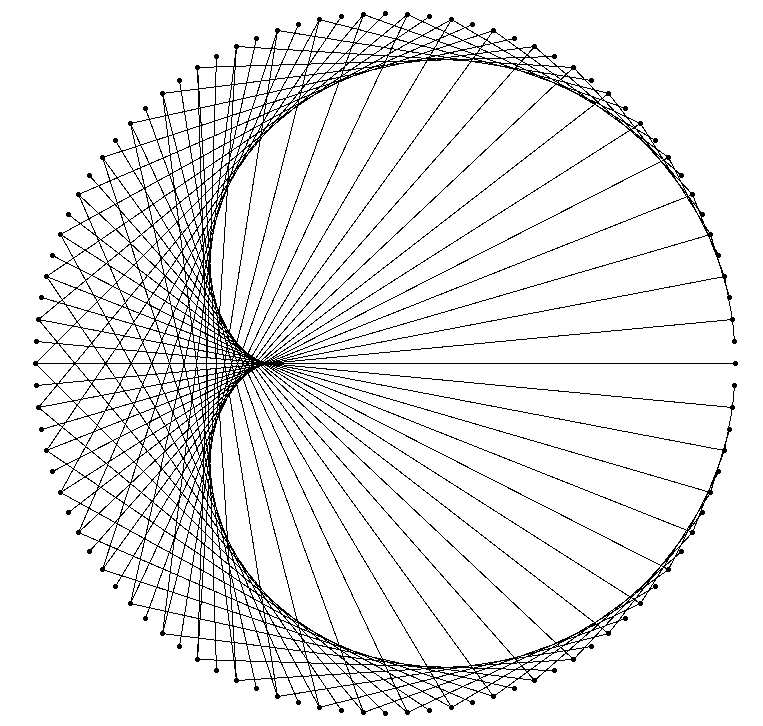
Plus précisément, on veut repésenter la table de multiplication de \(n\) avec \(p\) points placés sur un cercle. Pour fixer les idées, imaginons la table de \(n=2\) avec \(p=100\) points. Cela veut dire qu’on va représenter les 100 produits suivants :

\(1\times n2\), \(2\times 2\), \(3\times 2\), …, \(100\times 2\)

On commence par placer \(p\) points régulièrement espacés sur un cercle. Le premier point placé représente l’entier 1, le 2e point représente l’entier 2 et ainsi de suite jusqu’au \(p\)-ème point :

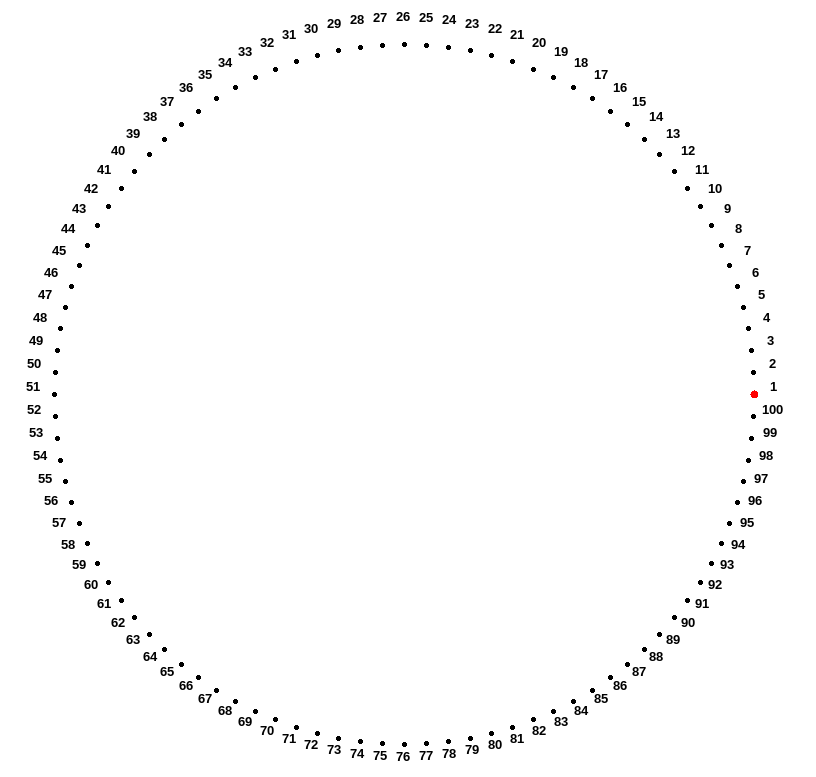
Pour représenter des entiers plus grands que \(p\), on continue à compter à partir du premier point, par exemple pour représenter \(242\), on utilise le point \(42\) puisque \(242=100+42\) ; de même, \(600\) est représenté par \(100\) ; plus généralement, un entier multiple de \(p\) est représenté par \(p\) et un entier non multiple de \(p\) est repésenté par son reste modulo \(p\).

Ensuite, chacun des \(p\) produits de la table de multiplication de \(n\) :

\(1\times n\), \(2\times n\), …, \(p\times n\)

sera représenté par un segment. Plus précisément, le produit \(k\times n\) est représenté par la corde AB où

• le point \(A\) représentant \(k\) sur le cercle,
• le point \(B\) représentant sur le cercle le résultat du produit \(k\times n\).

Voici un exemple, dans le cas \(n=2\) et \(p=100\), du produit \(73\times n\) :

Comme on a \(73\times 2=146\) qui est représenté par 46, on relie le point \(A\) représentant \(73\) et le point \(B\) représentant \(46\).

Lorsque les \(p\) « produits » sont dessinés, on obtient un motif, par exemple, la figure en début d’énoncé correspond à \(n=2\) et \(p=100\).

On demande d’écrire un programme de dessin d’une trentaine de lignes qui représente la figure pour \(n\) et \(p\) donnés.

On utilisera un cercle de centre \((0,0)\) et de rayon \(R=400\) mais qu’il sera inutile de tracer, cf. la figure en début d’énoncé. On rappelle que le point du cercle d’angle polaire \(t\) a pour coordonnées \((R\cos(t), R\sin(t))\). Pour faciliter le codage, les entiers représentés sur le cercle seront numérotés à partir de 0 (au lieu de 1 ci-dessus). On construira une liste sommets contenant les coordonnées des différents sommets du cercle en sorte que l’entier \(k=0,\dots, p-1\) soit représenté par sommets[k].

Une vidéo de Micmaths a popularisé cette représentation des tables de multiplication. Burkard Polster, dans la présentation d”une de ses vidéos, attribue la découverte de cette représentation à Simon Plouffe, cf. son article curves obtained with bn mod p.