\(\newcommand{\ds}{\displaystyle}\) \(\newcommand{\Frac}{\ds\frac}\) \(\renewcommand{\r}{\mathbb{ R}}\) \(\newcommand{\C}{\mathbb{ C}}\) \(\newcommand{\n}{\mathbb{ N}}\) \(\newcommand{\z}{\mathbb{ Z}}\) \(\newcommand{\Q}{\mathbb{ Q}}\) \(\newcommand{\N}{\mathbb{ N}}\) \(\newcommand{\n}{\mathbb{ N}}\) \(\newcommand{\ol}{\overline}\) \(\newcommand{\abs}[1]{\left| \,{#1} \right|}\) \(\newcommand{\pv}{\;;\;}\) \(\newcommand{\ens}[1]{\left\{ {#1} \right\}}\) \(\newcommand{\mens}[1]{\setminus\left\{ {#1} \right\}}\) \(\newcommand{\Par}[1]{\left({#1}\right)}\) \(\newcommand{\pe}[1]{\left\lfloor {#1} \right\rfloor}\) \(\newcommand{\trans}[1]{\,^t\!{#1}}\)

Construire, utiliser des fonctions : cours

Cours

Des instructions à la construction d’une fonction

Soit à écrire le code d’une fonction qui calcule le plus grand de deux nombres \(a\) et \(b\) donnés.

On va exposer le processus de transformation permettant de passer d’un code qui répond au problème mais qui n’utilise pas de fonction à un code équivalent mais placé dans une fonction.

On commence par écrire un code n’utilisant pas de fonction mais qui réponde à la question, quel que soit le choix pour a et b :

1a = 81
2b = 31
3
4if a >= b:
5    print(a)
6else:
7    print(b)

881

Il est ESSENTIEL d’utiliser des variables car ce sont elles qui vont devenir les paramètres de la fonction à construire.

On remarque que, en l’état :

  • le code ne peut être exécuté que pour deux choix particuliers de a et de b, cf. lignes 1-2 ;

  • le code ne place pas le maximum dans un variable mais se contente de l’afficher.

Il est essentiel que le code calcule correctement le maximum quelles que soient les valeurs choisies pour a et b. Par exemple, si dans le code ci-dessus, on change 81 en 2020 et 31 en 3000, le code doit encore afficher la bonne valeur (ici 3000).

Pour faciliter la conversion du code vers celui d’une fonction qui renvoie le maximum entre a et b, on peut placer le maximum dans une variable, par exemple m :

maximum_sans_fonction.py

1a = 81
2b = 31
3
4if a >= b:
5    m = a
6else:
7    m = b
8
9print(m)

1081

On va maintenant « convertir » ce code en celui d’une fonction. La fonction admet pour paramètres a et b et elle doit renvoyer le maximum m, donc le schéma de la fonction, que l’on va appeler f, est le suivant :

1def f(a, b):
2    # code inconnu ...
3    # ...
4    return m

Le code inconnu est obtenu en observant le code maximum_sans_fonction.py calculant le maximum m. Voici les deux codes comparés :

maximum_sans_fonction.py

1a = 81
2b = 31
3
4if a >= b:
5    m = a
6else:
7    m = b
8
9print(m)

maximum_fonction.py

 9def f(a, b):
10    if a >= b:
11        m = a
12    else:
13        m = b
14    return m
15
16a = 81
17b = 31
18print(f(a, b))

  • Lignes 1-2 : ces deux instructions ne servent pas dans le corps de f. Ces instructions qui définissaient a et b sont remplacées par l’en-tête de f ligne 10.

  • Lignes 4-7 : ces lignes sont préservées à l’identique dans le code de f.

  • Ligne 9 : comme f doit renvoyer le maximum m, on a remplacé l’affichage par une instruction return (ligne 15).

  • Lignes 17-19 : on teste f de la même façon que le code initial avait été exécuté pour deux valeurs de a et b, cf. lignes 1-2.

Enchaîner des fonctions

Il est assez fréquent que, dans un programme Python, une fonction fasse appel à une autre fonction qui elle-même fait appel à d’autres fonctions et ainsi de suite. On dit qu’on enchaîne les fonctions.

Par exemple, soit le code suivant :

enchainer_fonctions.py

 1def f(x):
 2    return g(x)*10
 3
 4def g(x):
 5    z=h(x) + k(x)
 6    print("g : ", z)
 7    return z
 8
 9def h(x):
10    z=x+2
11    print("h : ", z)
12    return z
13
14def k(x):
15    z=x+3
16    print("k : ", z)
17    return z
18
19a = 42
20print(a, f(a))

21h :  44
22k :  45
23g :  89
2442 890

  • Ligne 1 : une fonction f est définie et fait appel (au sens d’un appel de fonction) à une autre fonction g.

  • Ligne 4 : la fonction g est définie et fait elle-même appel à deux autres fonctions, définies plus bas, lignes 9 et 14.

  • Lignes 6, 11 et 16 : on a placé des instructions d’affichage pour mieux suivre l’enchaînement des appels des différentes fonctions.

  • Ligne 20 : l’appel f(42) est lancé.

    • Le code lignes 1-2 est exécuté mais la ligne 2 appelle la fonction g. Tant que la fonction g appelée ligne 2 n’aura pas renvoyé son résultat (la valeur de g(x)), la fonction f ne pourra rien renvoyer à l’expression appelante ligne 20 : on dit que la fonction f est en attente.

    • La fonction g appelle elle-même la fonction h et la fonction k.

    • Lorsque ces fonctions ont renvoyé leur résultat, la somme de ces résultats est placé dans la variable z de la définition de g. Puis g peut renvoyer son résultat à la fonction appelante, ici, la fonction f, à la ligne 2, qui elle-même peut renvoyer son résultat à l’appelant, ici la fonction print ligne 20.

Il peut être intéressant de visualiser la succession des appels de fonctions grâce au remarquable outil en ligne proposé par le site pythontutor. Ci-dessous une copie d’écran de l’outil appliqué au code ci-dessus :

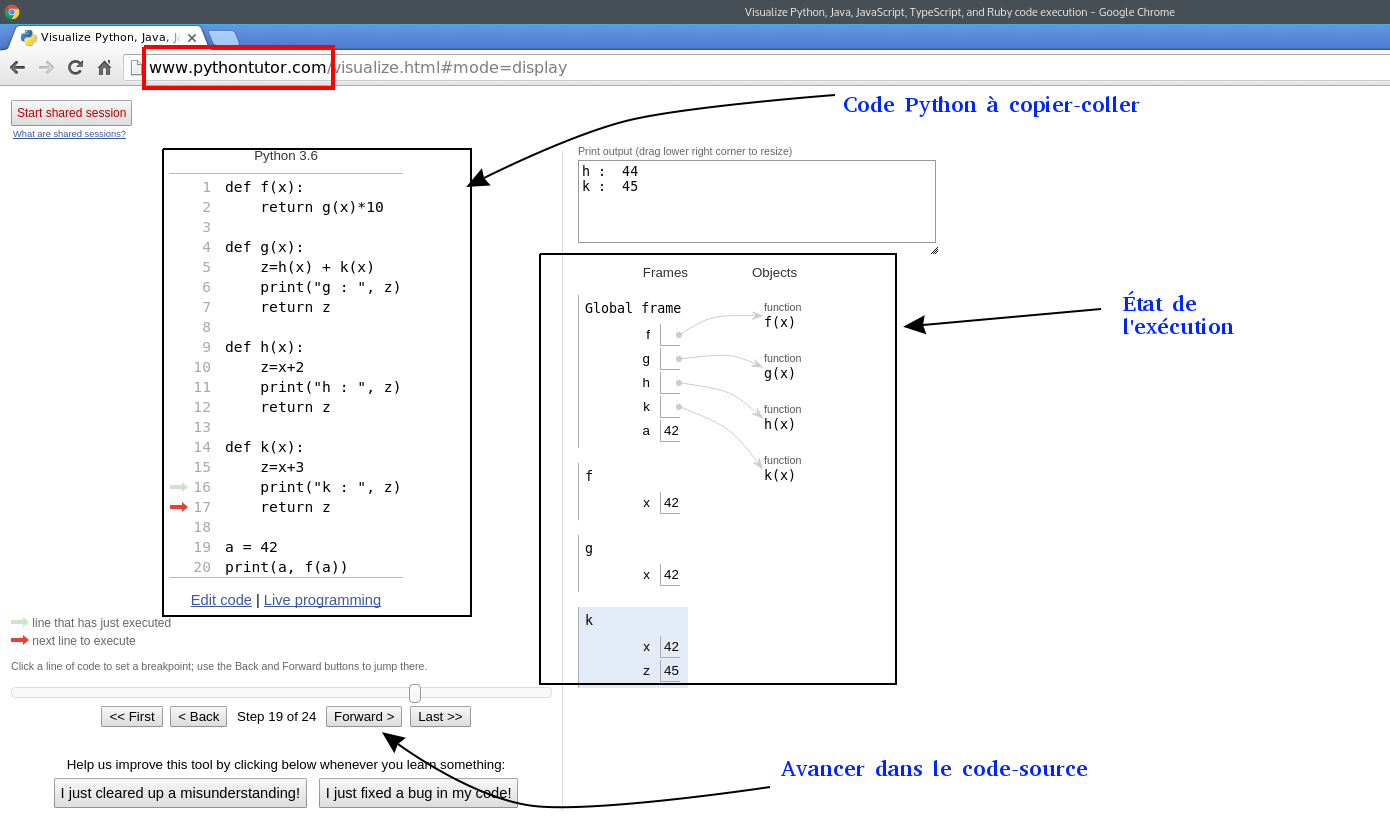
../../../_images/python_tutor_exemple_commentaires.png

Visualiser l’empilement des appels

Pile d’appels

On reprend le code enchainer_fonctions.py :

enchainer_fonctions.py

 1def f(x):
 2    return g(x)*10
 3
 4def g(x):
 5    z=h(x) + k(x)
 6    print("g : ", z)
 7    return z
 8
 9def h(x):
10    z=x+2
11    print("h : ", z)
12    return z
13
14def k(x):
15    z=x+3
16    print("k : ", z)
17    return z
18
19print(f(42))

Les appels de fonctions s’empilent pour former ce qu’on appelle la pile d’appels qu’on imagine comme des appels qui s’empilent de bas en haut.

  • Lignes 1-18 : la pile d’appels demeure vide lors de la première exécution de toutes ces lignes.

  • Ligne 19 : la fonction print est appelée, et donc la pile contient l’appel de print

  • Ligne 19 : la fonction f est appelée, et donc la pile contient, de bas en haut, l’appel de print puis l’appel de f

  • Ligne 2 : g est appelée, donc la pile contient de bas en haut, l’appel de print, l’appel de f et au-dessus l’appel de g

  • Ligne 5 : la fonction h est appelée, la pile contient de bas en haut : les appels de print, de f puis de g puis de h.

  • Ligne 5 : quand h renvoie sa valeur (lignes 12) à la fonction g qui l’a appelée, la fonction h quitte la pile d’appels. On dit alors que h dépile. La pile contient alors l’appel de print, de f puis l’appel de g qui sont en attente.

  • Ligne 5 : la fonction k est appelée donc la pile est constituée de bas en haut de : l’appel de print, l’appel de f, l’appel de g, l’appel de k.

  • k dépile (lignes 17) puis quand g renvoie z (lignes 7) à f (ligne 2) qui dépile aussi puis print (ligne 19) et la pile est à nouveau vide.

Ci-dessous, on peut observer l’évolution de la pile des appels.

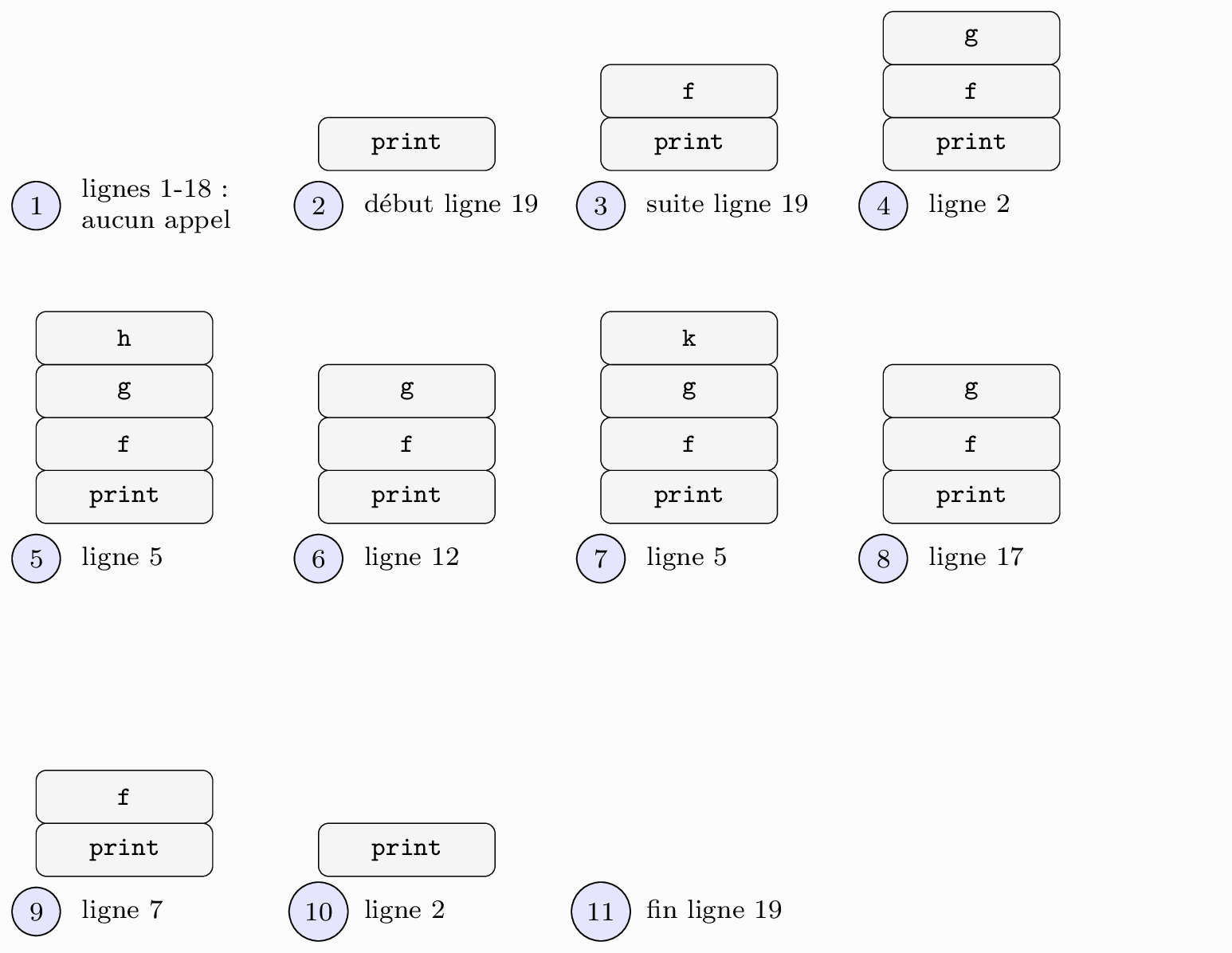
../../../_images/pile_appels.png

La pile des appels

La pile des appels est bien visible à l’aide d’un débogueur.

De l’usage des fonctions

Pour un débutant qui a déjà écrit du code Python mais sans utiliser encore la notion de fonction, écrire une fonction peut être une tâche difficile car il s’agit en général de transposer en code un raisonnement.

Intérêt d’écrire des fonctions

L’utilisation de fonctions présente les trois intérêts suivants :

  • le code est plus lisible que s’il n’est pas enveloppé dans une fonction car une fonction identifie clairement :

    • une tâche (virtuelle) à exécuter avec une interface constituée de paramètres que l’on donne à la fonction et d’un résultat (ce que renvoie l’instruction return),

    • d’un (ou plusieurs) appel(s) à la fonction ;

  • le code est réutilisable. Si on n’écrit pas le code dans une fonction, il faudrait récrire tout le code correspondant chaque fois que l’on souhaiterait effectuer la même tâche ;

  • le code est plus économique. Appeler une fonction, c’est une ligne de code qui en fait en appelle souvent plusieurs dizaines puisque l’appel équivaut à l’exécution de toutes les lignes de code de la fonction et des autres fonctions que la fonction appelle elle-même.

Découpage en tâches

Pour mieux organiser son code, le programmeur cherche souvent à découper la tâche à effectuer en plusieurs fonctions, chacune réalisant une certaine sous-tâche (on dit parfois « service » au lieu de « tâche » ou « sous-tâche »).

Lorsqu’on est débutant avec les fonctions, il n’est pas toujours facile d’arriver à découper son programme en fonctions pertinentes.

Lors de l’écriture d’une fonction f, le programmeur doit d’abord s’interroger sur l”interface de la fonction f :

  • quels seront les paramètres de f ? autrement dit, de quelles données la fonction f a-t-elle besoin ?

  • qu’est ce que la fonction f doit renvoyer ?

  • la fonction a-t-elle des effets de bords ?

Ensuite, il doit écrire le code de définition de la fonction f qui va être capable de réaliser la tâche : c’est ce qu’on appelle l”implémentation de la fonction.

Exemple

Par exemple, soit le tableau de Pascal :

../../../_images/triangle_pascal.png

Le triangle de Pascal

Comment ça marche ? Chaque élément z d’une ligne s’obtient comme somme des deux termes au-dessus et à gauche de l’élément z. Par exemple, à la ligne 7, on a : 35 = 20 + 15. On veut écrire un programme qui affiche le tableau de Pascal jusqu’à sa \(n^\text{e}\) ligne .

Plus précisément, voici les règles de construction du Tableau de Pascal. Le Tableau de Pascal est une suite de lignes telles que :

  • la 1ère ligne est 1 1 ;

  • chaque ligne commence et se termine par le nombre 1 ;

  • pour chaque élément \(z\) qui ne figure pas aux extrémités d’une ligne \(L\) du tableau, on a \(z=x+y\) où \(x\) est le terme sur la ligne précédente de \(L\) et situé au-dessus de \(z\) et \(y\) est le voisin de gauche de \(x\).

Objectif : écrire une fonction pascal(n) qui prend en paramètre un numéro \(\mathtt{n}\) de ligne et qui affiche les \(n\) premières lignes du tableau de Pascal.

Pour afficher une ligne, il suffit de connaître la précédente (disons L) et d’appliquer les règles de construction du Tableau de Pascal. Cette tâche sera accomplie par une fonction ligne_suivante(L). Pour bien comprendre ce qui suit, il faut savoir qu’une ligne du tableau de Pascal sera représentée dans le programme par une liste d’entiers et donc construire le tableau de Pascal revient à construire une liste de listes.

Voici un code possible de la fonction ligne_suivante(L), accompagné d’un test :

 1def ligne_suivante(L):
 2    LL=[1]
 3    n=len(L)
 4    for k in range(1, n):
 5        LL.append(L[k-1]+L[k])
 6    LL.append(1)
 7    return LL
 8
 9L=[1, 3, 3, 1]
10print(ligne_suivante(L))

11[1, 4, 6, 4, 1]

  • Ligne 2: LL est la future ligne suivante et au départ une liste contenant juste le 1 initial de chaque ligne et qui va être remplie au fur et à mesure.

  • Lignes 6 : l’autre extrémité de chaque ligne du tableau vaut 1.

  • Lignes 4-5 : la règle de construction du terme LL[k] de la ligne suivante de L dans le Tableau de Pascal. On sait que LL[k] est la somme des deux termes de L situés en haut et à gauche de LL[k].

  • Ligne 7 : la fonction doit renvoyer la nouvelle ligne.

  • Lignes 9-11 : un test, positif puisque la ligne suivante de la ligne 1 3 3 1 est bien 1 4 6 4 1.

La fonction pascal(n) va utiliser la fonction ligne_suivante(L) dans une boucle pour donner une première version du tableau de Pascal que l’on va affiner ensuite :

 1def ligne_suivante(L):
 2    LL=[]
 3    LL.append(1)
 4    n=len(L)
 5    for k in range(1, n):
 6        LL.append(L[k-1]+L[k])
 7    LL.append(1)
 8    return LL
 9
10def pascal(n):
11    L=[1, 1]
12    print(L)
13    for i in range(0, n-1):
14        LL=ligne_suivante(L)
15        L=LL
16        print(L)
17
18pascal(10)

19[1, 1]
20[1, 2, 1]
21[1, 3, 3, 1]
22[1, 4, 6, 4, 1]
23[1, 5, 10, 10, 5, 1]
24[1, 6, 15, 20, 15, 6, 1]
25[1, 7, 21, 35, 35, 21, 7, 1]
26[1, 8, 28, 56, 70, 56, 28, 8, 1]
27[1, 9, 36, 84, 126, 126, 84, 36, 9, 1]
28[1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1]

  • Ligne 10 : il y a n lignes à afficher

  • Lignes 11-12 et 19 : on affiche la 1ère ligne du Tableau de Pascal

  • Ligne 13 : il reste n-1 lignes à afficher d’où le range(n-1).

  • Ligne 14 : L est la ligne courante, LL la ligne suivante, renvoyée par la fonction ligne_suivante

  • Ligne 15 : le point-clé du programme : on prépare le tour suivant dans la boucle en mettant à jour la ligne courante. Il aurait été possible de remplacer le code des lignes 14-15 par l’unique ligne L=ligne_suivante(L).

  • Ligne 16 : affichage de la ligne courante.

  • Lignes 18 et 19-28 : on reconnaît bien les 10 premières lignes du Tableau de Pascal.

On se rend compte en regardant l’affichage obtenu qu’il peut être amélioré pour faire afficher juste des nombres, sans virgules ni crochets. Pour cela, il suffit d’écrire une fonction afficher_ligne dont la tâche est d’afficher le contenu d’une liste sur un seule ligne en séparant les éléments par une seul espace :

1def afficher_ligne(L):
2    for i in range(len(L)):
3        print(L[i], end = " ")
4    print()
5
6afficher_ligne([1, 4, 6, 4, 1])
7afficher_ligne([1, 8, 28, 56, 70, 56, 28, 8, 1])

81 4 6 4 1
91 8 28 56 70 56 28 8 1

Il ne reste plus qu’à remplacer l’affichage print(L) de la fonction pascal(n) à la ligne 16 par afficher_ligne(L) pour obtenir le programme attendu :

 1def ligne_suivante(L):
 2    LL=[1]
 3    n=len(L)
 4    for k in range(1, n):
 5        LL.append(L[k-1]+L[k])
 6    LL.append(1)
 7    return LL
 8
 9def pascal(n):
10    L=[1, 1]
11    afficher_ligne(L)
12    for i in range(0, n-1):
13        L=ligne_suivante(L)
14        afficher_ligne(L)
15
16def afficher_ligne(L):
17    for i in range(0, len(L)):
18        print(L[i], end = " ")
19    print()
20
21pascal(10)

221 1
231 2 1
241 3 3 1
251 4 6 4 1
261 5 10 10 5 1
271 6 15 20 15 6 1
281 7 21 35 35 21 7 1
291 8 28 56 70 56 28 8 1
301 9 36 84 126 126 84 36 9 1
311 10 45 120 210 252 210 120 45 10 1

L’affichage pourrait être encore amélioré pour faire apparaître des colonnes bien alignées.

Exercice type : Périodes de l’année

Dans cet exercice, on va considérer des périodes sous la forme

\(\mathtt{a}\) années, \(\mathtt{m}\) mois et \(\mathtt{j}\) jours

où \(\mathtt{1\leq m \leq 12}\) et \(\mathtt{1\leq j \leq 30}\) où \(\mathtt{a, m}\) et \(\mathtt{j}\) sont des entiers. Pour simplifier, on considérera qu’une année comportera 12 mois et qu’un mois dure toujours 30 jours (et donc qu’une année comporte 360 jours et non 365).

  1. Écrire une fonction amj_to_j(a, m, j) qui retourne le nombre de jours d’une période exprimée en années, mois et jours. Vérifier que 27 ans, 9 mois et 10 jours correspondent à 10000 jours.

  2. Cette question est indépendante de ce qui précède. Dans cette question, l’usage de la méthode append est inapproprié.

    Écrire une fonction j_to_amj(jours) qui prend en paramètre une période exprimée en jours et la retourne exprimée en années, mois et jours sous forme de liste [a, m, j]. Bien sûr, on aura \(\mathtt{1\leq m \leq 12}\) et \(\mathtt{1\leq j \leq 30}\). Vérifier que 10000 jours correspondent à 27 ans, 9 mois et 10 jours.

  3. Cette question est indépendante de ce qui précède. Écrire une procédure afficher_periode qui prend en paramètre une liste de 3 entiers correspondant à une période de \(\mathtt{a}\) années, \(\mathtt{m}\) mois et \(\mathtt{j}\) jours et qui affiche

    a années m mois et j jours

    Par exemple, afficher_periode([27, 9, 1]) affiche exactement :

    27 années 9 mois et 1 jours

  4. Votre réponse à cette question doit utiliser les fonctions définies dans les questions précédentes. Cette question ne demande pas de définir de nouvelle fonction.

    Un père a un âge de 42 ans, 4 mois et 2 jours et sa fille a un âge de 14 ans 6 mois et 22 jours. Écrire un programme qui affiche la différence d’âge, exprimée en années, mois et jours, entre le père et sa fille.

    Il est attendu que votre code tienne sur une seule ligne.

    Solution

  1. D’après les hypothèses simplificatrices de l’énoncé, le nombre de jours dans une période de a années, m mois et j jours est donné par la formule :

    360*a+30*m+j

    d’où le code :

    def amj_to_j(a, m, j):
    return 360*a+30*m+j

print(amj_to_j(10, 4, 22))

    3742

    • Ligne 5 : on retrouve bien le nombre de jours annoncés.

  2. Une périodes jours contient jours // 360 années entières avec un reliquat de jours % 360 jours. De la même façon, on convertit ce reliquat de jours en mois et jours. D’où le code :

    def j_to_amj(jours):
    a=jours//360
    r=jours%360
    m=r//30
    j=r%30
    return [a, m, j]

print(j_to_amj(10000))

    [27, 9, 10]

    • Ligne 9 : on retrouve bien 27 ans, 49 mois et 10 jours.

  3. Il s’agit d’écrire une procédure d’affichage. La fonction reçoit un argument sous forme de liste [j, m, a]. Mais le paramètre ne peut avoir cette forme, un paramètre étant toujours un nom de variable, disons ici periode. Dans le code de définition de la fonction, on accède aux années, mois et jours en utilisant un indice puisque periode représente une liste de 3 entiers. D’où le code :

    def afficher_periode(periode):
    print(periode[0], "années",  periode[1],
          "mois", "et", periode[2], "jours")

afficher_periode([27, 9, 1])

    27 années 9 mois et 1 jours

  4. Pour calculer un écart entre deux durées, il suffit de

    • convertir chaque durée en jours avec la fonction amj_to_j

    • de faire la différence des durées en jours

    • de reconvertir cette durée en jours en une période en années, mois et jours avedc la fonction j_to_amj.

    Enfin, il restera à afficher la durée avec la fonction afficher_periode.

    D’où le code :

    afficher_periode(j_to_amj(amj_to_j(42, 4, 2)-amj_to_j(9, 9, 28)))

    32 années 6 mois et 9 jours

Modification par une fonction d’un de ses arguments

Une fonction peut-elle modifier un objet qu’elle reçoit en argument ? La réponse doit être nuancée en fonction du sens que l’on donne au verbe modifier.

En aucun cas, une fonction ne peut substituer un autre objet à un objet qu’elle reçoit en argument.

Examinons une tentative de modification par une fonction d’un objet que la fonction reçoit en argument. Soit par exemple le code ci-dessous

1def f(x):
2    x = 42
3
4a=10
5print(a)
6f(a)
7print(a)

810
910

  • Lignes 4 et 8 : la valeur de a avant l’appel

  • Lignes 2 et 6 : l’action de f qui tente de modifier l’objet reçu en argument

  • Ligne 7 : la valeur de a est inchangée et c’est le même objet 10 que celui vers lequel a se référait avant l’appel.

La fonction f « affecte » 42 au paramètre x. Si on passe en argument à f une autre valeur comme 10, cette valeur va-t-elle être remplacée par 42 ? Non, comme le montre l’affichage ci-dessus.

Le schéma ci-dessous montre les affectation effectuées tout du long du programme ci-dessus :

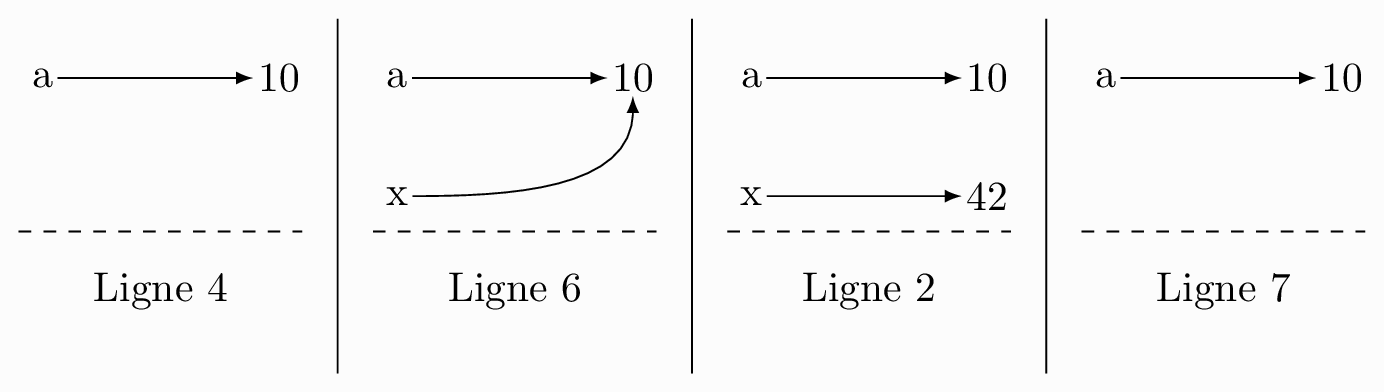
../../../_images/parametres_affectation.png

Passage des paramètres par affectation

Pour comprendre le comportement de f et pourquoi a n’est pas modifié, il suffit de se rappeler que l’action d’un passage des arguments en Python est une transmission par affectation et donc le code ci-dessus est équivalent à :

1a=10
2print(a)
3
4# ----- Équivalent de l'action f(a)
5x = a
6x = 42
7# -----
8
9print(a)

1010
1110

Les affectations x=a et x=42 ne peuvent pas remplacer a par 42 ; en effet, x=42 ne fait que créer un nouvel objet 42 et lui associer le nom x, autrement dit, la variable x ne référence plus l’objet 10 qu’elle référait ligne 5. On voit que ces affectations ne peuvent modifier a qui lui ne subit aucune affectation.

À défaut de remplacer un objet par un autre, une fonction peut-elle modifier le contenu d’un objet ? La réponse dépend de la nature de l’objet.

Si une fonction reçoit en argument un objet immuable comme un entier ou une chaîne, par définition, l’objet ne pourra pas être modifié, et a fortiori par f.

Le cas d’un objet mutable

Si une fonction reçoit en argument un objet mutable comme une liste, l’objet pourra être modifié par la fonction. Voici un exemple où une liste est modifiée par une fonction :

 1def f(M):
 2    M[0] = 42
 3
 4L=[81, 12, 31, 65]
 5print(L)
 6print()
 7
 8f(L)
 9
10print(L)

11[81, 12, 31, 65]
12
13[42, 12, 31, 65]

  • f est appelée sur une liste d’entiers

  • l’action de consiste à remplacer le premier élément de M par 42

  • une fois l’appel de f terminé, on constate que l’objet L placé en paramètre a été modifié.

Une fois de plus, le mode de passage des arguments par affectation propre à Python permet de prévoir ce comportement. En effet le code ci-dessus est équivalent à

 1L=[81, 12, 31, 65]
 2print(L)
 3print()
 4
 5# ---- Début de l'action de f
 6
 7M=L
 8M[0]=42
 9
10# ---- Fin de l'action de f
11
12print(L)

13[81, 12, 31, 65]
14
15[42, 12, 31, 65]

L’exemple ci-dessus ne foit pas faire croire que l’argument a été changé : après appel, L référence toujours le même objet. La différence, c’est que le contenu de L a changé.

Boucle for et return

Le corps d’un boucle peut contenir n’importe quelle instruction ; en particulier, si une boucle for apparaît dans la définition d’une fonction, elle peut être interrompue par une instruction return.

Par exemple, soit à définir une fonction qui prend une liste L en paramètre et renvoie True si L ne contient aucun entier strictement négatif et False sinon :

 1def f(L):
 2    for i in range(len(L)):
 3        if L[i] < 0:
 4            return False
 5    return True
 6
 7L= [31, 82, -42, 32, -81]
 8print(L, f(L))
 9
10print("=========================")
11
12L= [31, 82, 421, 32, 81]
13print(L, f(L))

14[31, 82, -42, 32, -81] False
15=========================
16[31, 82, 421, 32, 81] True

  • Lignes 1-5 : la fonction f répond au problème posé.

  • Ligne 4 : une instruction return interrompt l’exécution de la fonction.

  • Lignes 3-4 : la liste L est parcourue et si un terme de la liste L est un nombre négatif, le parcours de la liste ainsi que l’exécution de la fonction sont interrompus et la fonction renvoie False

  • Ligne 5 : si la liste L est parcourue sans que jamais le parcours ne soit interrompu par la détection d’un nombre négatif dans la liste, la fonction f se termine en renvoyant True puisque tous les termes de L sont positifs ou nuls.

Résumons le schéma ci-dessus :

  • placement d’une boucle for dans une fonction ;

  • parcours avec la boucle for d’une liste jusqu’à ce qu’une certaine condition soit vérifiée ;

  • interruption de la boucle et de la fonction par une instruction return renvoyant un booléen.

L’intérêt de ce schéma est que le parcours de la liste est optimal : le parcours est interrompu dès que la réponse est connue, ce qui n’est pas le cas de la méthode utilisant un simple drapeau.

Exercice type : Grille en équerres

  1. Écrire une procédure \(\mathtt{f(i, n)}\) où \(\mathtt{i, n}\) sont des entiers tels que \(\mathtt{1\leq i\leq n}\) qui affiche, sur une même ligne, \(\mathtt{n}\) entiers séparés par une espace dont les \(\mathtt{i}\) premiers entiers sont \(\mathtt{1,2,\dots, i}\) et les \(\mathtt{n-i}\) derniers sont tous identiques à l’entier \(\mathtt{i}\). Par exemple, \(\mathtt{f(5,9)}\) doit afficher la ligne suivante :

    1 2 3 4 5 5 5 5 5

  2. En déduire une procédure \(\mathtt{g(n)}\) qui affiche une grille carrée « en équerres » telle que celle qui figure ci-contre (dans cet exemple \(\mathtt{n=9}\)). Deux nombres sur une même ligne seront séparés par une espace. Observez bien comment sont placés « en équerres » les nombres 1, 2, etc.

    1 1 1 1 1 1 1 1 1
1 2 2 2 2 2 2 2 2
1 2 3 3 3 3 3 3 3
1 2 3 4 4 4 4 4 4
1 2 3 4 5 5 5 5 5
1 2 3 4 5 6 6 6 6
1 2 3 4 5 6 7 7 7
1 2 3 4 5 6 7 8 8
1 2 3 4 5 6 7 8 9

    Solution

  1. Pour calculer \(\mathtt{f(i, n)}\), il faut effectuer deux actions :

    • la génération des entiers de 1 à \(\mathtt{i}\) ;

    • la répétition \(\mathtt{n-i}\) fois de l’entier \(\mathtt{i}\).

    Ces deux actions répètent quelque chose et donc se codent chacune avec une boucle for. D’où le code :

    def f(i,n):
    for j in range(0, i):
        print(j+1, end=' ')

    for k in range(0,n-i):
        print(i, end = ' ')

f(5,9)
print()
print()
f(1,9)

    1 2 3 4 5 5 5 5 5

1 1 1 1 1 1 1 1 1

    • Lignes 3 et 6 : pour séparer chaque entier du suivant par juste un espace, on utilise l’argument nommé end=" " pour la fonction print.

  2. Pour afficher le motif 2D demandé, il suffit de remarquer que la 1re ligne du motif est f(1, n), la 2e ligne est f(2, n) et ainsi de suite. Donc, pour afficher le motif, il suffit de répéter avec une boucle for l’affichage de chaque ligne. D’où le code :

    def f(i,n):
    for j in range(0, i):
        print(j+1, end=' ')

    for k in range(0,n-i):
        print(i, end = ' ')

def g(n):
    for k in range(n):
        f(k+1,n)
        print()

g(9)

    qui affiche

    1 1 1 1 1 1 1 1 1
1 2 2 2 2 2 2 2 2
1 2 3 3 3 3 3 3 3
1 2 3 4 4 4 4 4 4
1 2 3 4 5 5 5 5 5
1 2 3 4 5 6 6 6 6
1 2 3 4 5 6 7 7 7
1 2 3 4 5 6 7 8 8
1 2 3 4 5 6 7 8 9

Variables locales

La notion de variable locale

variable_locale.py

1def f(x):
2    y=x+1
3    return 10*y
4
5print(f(8))

Lorsqu’on définit une fonction, ici la fonction f lignes 1-3, les variables dites locales à la fonction f sont

  • les variables données en paramètre, comme x (ligne 1)

  • les variables créées dans la définition de la fonction, par exemple y à la ligne 2.

Les objets que représentent ces variables n’existent que pendant l’exécution de la fonction f, c’est-à-dire uniquement lors de l’appel de la fonction f. Ainsi, la variable x n’a pas d’existence tant que f n’a pas été appelée. En outre, après la fin de l’exécution de la fonction, la variable x n’a plus d’existence non seulement en mémoire mais aussi dans le code-source. Les variables locales disparaissent avec l’exécution de la fonction.

Tentative d’accès à une variable locale

Le caractère local de variables comme x ou y signifie que ces variables ne sont pas connues à l’extérieur du code de la fonction f. Si on tente d’y accéder, on obtient une erreur.

Voici deux codes qui illustrent des tentatives de lecture de variables locales :

1def f(x):
2    y=x+1
3    return 10*y
4
5print(f(8))
6print(x)

 790
 8Traceback (most recent call last):
 9  File "a.py", line 6, in <module>
10    print(x)
11NameError: name 'x' is not defined

  • Lignes 5 et 1 : la variable x prend la valeur 8 pendant l’exécution de f pendant l’appel ligne 5.

  • Ligne 11 : pourtant, la variable x N’est PAS reconnue en dehors du code de définition de la fonction f.

  • Ligne 7 : le résultat de l’affichage de la ligne 5.

1def f(x):
2    y=x+42
3    z=10
4    return 2*y+z
5
6print(f(8))
7print(z)

 8110
 9Traceback (most recent call last):
10  File "a.py", line 7, in <module>
11    print(z)
12NameError: name 'z' is not defined

  • Ligne 3 : définition de la variable locale z de la fonction f.

  • Ligne 6 : pendant l’appel de f, la variable z est utilisée

  • Lignes 7 et 12 : après l’appel de f , la variable z cesse complètement d’exister.

Remède

Une variable locale à une fonction n’a pas vocation à être accédée depuis l’extérieur de la fonction. Si on veut accéder à une variable locale (en fait à son contenu), il faut que la fonction renvoie le contenu de cette variable locale ou renvoie un objet qui permette d’accéder à la valeur de cette variable locale.

Variables globales

Soit le code suivant :

1def f(x):
2    print(z)
3    return z + x
4
5z=42
6
7print(f(8))

842
950

La variable z déclarée à la ligne 5 en dehors de toute fonction : on dit que z est une variable globale. La fonction f définie à la ligne 1 a accès à cette variable (lignes 2-3). Observons que :

  • la variable globale z est définie après la définition de f. En fait ce qui compte, c’est que z soit définie avant l’appel (ligne 7) à la fonction f.

  • l’accès à la variable globale z se fait en lecture et non en écriture ie la variable z n’est pas modifiée par la fonction f.

Quand on débute en programmation, et qu’on commence à manipuler des fonctions, il est conseillé d’éviter d’utiliser des variables globales. L’intérêt d’une fonction est de constituer un environnement autonome d’exécution : en principe, une fonction ne doit dépendre d’aucun élément extérieur autre que des appels éventuels à d’autres fonctions.

Si, pour des raisons exceptionnelles, une fonction est amenée à utiliser une variable globale, il est souhaitable, pour des raisons de lisibilité, de déclarer ces variables en début de la zone d’édition du code source, avant les fonctions qui y font appel.

Constantes placées en variables globales

Limiter l’usage de variables globales est considéré comme une bonne pratique de programmation. Utiliser des constantes en variables globales est un cas toléré. Il s’agit de variables qui référencent des objets qui ne changeront pas durant toute la vie du programme.

Un programme utilisant une valeur de \(\pi\) pour calculer des aires ou des volumes pourra définir \(\pi\) comme variable globale. Voici un exemple :

 1PI = 3.1415926
 2
 3def disque(r):
 4    return PI * r * r
 5
 6def sphere(r):
 7    return 4 * PI * r * r
 8
 9print(disque(10))
10print(sphere(10))

11314.15926
121256.63704

  • Ligne 1 : constante déclarée en variable globale.

  • Lignes 4 et 7 : utilisation de PI dans des fonctions.

L’usage veut que des variables globales référençant des constantes soient écrites en début de fichier et en majuscules.

Fonction non appelée

Soit le code suivant :

1z=10
2
3def f(x):
4    print(10 * x)
5
6print(z+1)

711

  • Lignes 3-4 : une fonction f est définie mais cette fonction n’est appelée nulle part dans le programme.

En pratique, un code n’a pas de raison de définir une fonction sans appeler cette fonction avec des arguments. Toutefois, cela signifie que vous pouvez, sans danger, écrire la définition d’une fonction qui, par exemple, serait inachevée, ou qui ne marcherait pas encore ou qui ne serait qu’une ébauche ou un template d’un programme à exécuter ultérieurement.

Mais il existe des raisons plus sérieuses à écrire des fonctions sans les appeler dans le fichier où les fonctions sont définies : il est possible d’appeler ces fonctions depuis un autre fichier Python.

Le passage des arguments par affectation

Soit le code :

1def f(d,u):
2    N = 10 * d + u
3    return N
4
5print(f(4,2))

642

  • Lignes 1-3 : une définition de fonction

  • Ligne 5 : un appel de la fonction avec les arguments 4 et 2

Lors de l’appel f(4,2) ligne 5 dans le code ci-dessus, la transmission des arguments 4 et 2 aux paramètres de f est effectuée exactement comme dans le code ci-dessous :

1d = 4
2u = 2
3
4N = 10 * d + u
5
6print(N)

Le lien qui existe entre un paramètre, par exemple d, son argument 4, est une affectation (ligne 1), d’où la terminologie, propre à Python de passage des arguments par affectation. L’objet que le paramètre d reçoit au moment de l’exécution de la fonction f est exactement le même objet que l’argument. Non seulement, l’objet reçu a la même valeur, mais, mieux, ils sont identiques.

Pour se rendre compte qu’il s’agit du même objet, on utilise la fonction standard id qui permet d’identifier un objet en renvoyant son « identifiant » unique afin de le discerner d’autres objets :

1def f(d,u):
2    print("id(d) ->", id(d))
3    N = 10 * d + u
4    return N
5x=4
6print("id(x) ->", id(x))
7
8print(f(x,2))

 9id(x) -> 139697383176736
10id(d) -> 139697383176736
1142

  • Lignes 1-4 : on a modifié la fonction f d’un code antérieur pour qu’elle affiche l’id de l’objet qu’elle reçoit pour le paramètre d

  • Ligne 2 : on affiche l’id de l’objet associé à la variable x, plus bas l’objet 4.

  • Lignes 9-10 : on constate qu’il s’agit des mêmes objets.

En particulier, le passage des arguments lors de l’appel d’une fonction se fait sans copie de l’objet. Le fait qu’il n’y ait pas de copie est une garantie d’efficacité. Toute action que la fonction peut avoir sur un objet lors de son exécution doit pouvoir être exécutée comme si l’objet était accédé par une affectation.