Boucle for : introduction¶

Le code suivant présente un exemple d’utilisation d’une boucle for :

for.py

1
2
3

for i in range(0, 4):
    print("Bonjour !")
    print("---------")

 4
 5
 6
 7
 8
 9
10
11

Bonjour !
---------
Bonjour !
---------
Bonjour !
---------
Bonjour !
---------

Les lignes 1-3 constituent une instruction for. On observe (lignes 4-11) que le message Bonjour ! suivi du séparateur --------- est affiché 4 fois. Si on changeait la valeur 4 à la ligne 1 en la valeur 5 le message serait répété 5 fois.

Ici, la boucle for a permis de répéter une action un certain nombre de fois.

1
2
3

for i in range(0, 4):
    print("Bonjour !")
    print("---------")

1
2

for i in range(0, 5):
    print("Message n°", i+1, ":", "Bonjour !")

1
2
3
4
5

Message n° 1 : Bonjour !
Message n° 2 : Bonjour !
Message n° 3 : Bonjour !
Message n° 4 : Bonjour !
Message n° 5 : Bonjour !

Répéter une action \(n\) fois avec une boucle for¶

La boucle for et la fonction range permettent typiquement de répéter une action n fois où n est fixé avant le démarrage de la boucle.

Par exemple, soit à afficher un carré de côté 10 comme ci-dessous :

* * * * * * * * * *
* * * * * * * * * *
* * * * * * * * * *
* * * * * * * * * *
* * * * * * * * * *
* * * * * * * * * *
* * * * * * * * * *
* * * * * * * * * *
* * * * * * * * * *
* * * * * * * * * *

L’affichage consiste en la répétition 10 fois de l’affichage d’une ligne de la forme

* * * * * * * * * *

où les 10 étoiles sont séparées par un espace.

Le code Python pourrait être :

z="* * * * * * * * * *"
for i in range(10):
    print(z)

De même, soit à afficher les 10 premiers multiples de 5 en commençant par 75 :

\(75\), \(75 +5=80,\) \(75+10=85\), etc.

Donc, un code répondant à la question est le suivant :

1
2
3

d = 75
for i in range(10):
    print(d + 5 * i)

 4
 5
 6
 7
 8
 9
10
11
12
13

75
80
85
90
95
100
105
110
115
120

• Ligne 2 : typiquement, on utilise range(10) pour exprimer qu’une action va être exécutée 10 fois. Le nombre de répétitions (ici 10) est connu avant d’effectuer la boucle for.
• Ligne 3 : l’action (d’afficher le multiple) est à effectuer 10 fois.

Règle : Si un programme répète une action et si le nombre de répétitions à effectuer est connu à l’avance, le programme utilise une boucle for avec la syntaxe suivante :

for i in range(n):
    # action a coder ICI

Cela fait partie des idiomes de la programmation impérative et, en particulier, de la programmation en Python.

Affichage sur une même ligne et boucle for¶

Soit à réaliser avec une boucle for l’affichage suivant :

----------------
0 1 2 3 4 5 6 7 8 9
----------------

Pour éviter le saut de ligne après l’affichage de chaque entier et pour séparer chaque nombre du précédent d’une espace, on utilise l’argument nommé end = " " :

1
2
3
4
5

print("----------------")
for i in range(10):
    print(i, end = " ")
print()
print("----------------")

6
7
8

----------------
0 1 2 3 4 5 6 7 8 9
----------------

• Ligne 7 : chaque entier est séparé du précédent par un espace. Aucun saut de ligne n’est effectué lors de l’exécution de la boucle.
• Ligne 4 : permet d’effectuer un saut de ligne entre le dernier chiffre affiché (ligne 7) et la ligne formée de pointillés (ligne 8)

Omettre l’appel à print en sortie de boucle provoque un affichage incorrect :

1
2
3
4

print("----------------")
for i in range(10):
    print(i, end = " ")
print("----------------")

5
6

----------------
0 1 2 3 4 5 6 7 8 9 ----------------

Pour bien comprendre la rôle de end=" " dans print(i, end=" "), il suffit d’observer le résultat du code ci-dessous où le end=" " est remplacé par, par exemple, la chaîne end="xxx" :

1
2
3
4
5

print("----------------")
for i in range(10):
    print(i, end="xxx")
print()
print("----------------")

6
7
8

----------------
0xxx1xxx2xxx3xxx4xxx5xxx6xxx7xxx8xxx9xxx
----------------

Itérer sur des entiers consécutifs¶

La fonction built-in range permet de générer automatiquement des entiers consécutifs, comme les entiers 6, 7, 8 et 9 :

r=range(6, 10)
for i in r:
    print(i)

6
7
8
9

En pratique, on n’utilise pas la variable intermédiaire r ci-dessus et on écrit plutôt :

for i in range(6, 10):
    print(i)

Bien observer que le deuxième argument de la fonction range (dans l’exemple, c’est 10) est exclu des nombres générés. Toutefois, le nombre d’entiers générés par range(a,b) est \(\mathtt{b-a}\) (en supposant que \(\mathtt{a\leq b}\)).

Si \(\mathtt{n\geq 0}\) est un entier, l’expression range(n) est un raccourci syntaxique pour range(0,n) :

for i in range(3):
    print(i)

0
1
2

Calcul d’une somme¶

La méthode pour calculer une somme de nombres doit être très bien connue tant ce type de problème est fréquent. Illustrons par un exemple.

On se donne un entier \(\mathtt{n\geq 1}\) et on demande de calculer la somme de tous les cubes des entiers entre \(\mathtt{1}\) et \(\mathtt{n}\). Par exemple, si \(\mathtt{n = 9}\) alors la somme vaut

\(1^3+2^3+3^3+\dots+8^3+9^3=2025\)

L’algorithme, consiste à calculer successivement les sommes partielles suivantes

\(1^3\), \(1^3+2^3\), \(1^3+2^3+3^3\), …

jusquà la somme voulue, chaque somme s’obtenant à partir de la précédente en additionnant un nombre (un cube pour être précis).

En Python, on procède comme suit :

• on définit une variable « accumulatrice » \(\mathtt{s}\), initialisée à 0 et qui, en fin de programme, vaudra la somme cherchée ;
• on parcourt avec une boucle for tous les entiers entre \(\mathtt{1}\) et \(\mathtt{n}\) inclus ;
• lorsque, dans la boucle, on traite l’entier k entre 1 et \(\mathtt{n}\), on augmente la somme partielle \(\mathtt{s}\) de la valeur \(\mathtt{k^3}\). Pour cela, on écrit l’instruction s = s + k**3

D’où le code suivant :

n = 9

s = 0

for k in range(1, n+1):
    s = s + k**3

print(s)

2025

Exercice type : De 42 en 42¶

Afficher les entiers obtenus en comptant 10 fois de 42 en 42 à partir de 421.

Solution

Il s’agit de répéter une action 10 fois, donc il est assez naturel de chercher un code ayant la forme suivante :

1
2
3

for i in range(10):
    # Code
    # à compléter

Les nombres à afficher vont évoluer dans une variable x initialisée à 421. A chaque tour de boucle, x est incrémenté de 42. D’où le code :

1
2
3
4

x=421
for i in range(10):
    print(x)
    x = x + 42

 5
 6
 7
 8
 9
10
11
12
13
14

421
463
505
547
589
631
673
715
757
799

Variante :

1
2

for i in range(10):
    print(421 + i * 42)

Exercice type : Comptage de 5 en 5¶

On compte de 5 en 5 tous les entiers entre deux entiers \(a\) et \(b\) (bornes incluses) avec \(a\leq b\), par exemple \(a=1914\) et \(b=2020\). À l’aide d’une boucle for, déterminer combien d’entiers on compte ainsi (pour l’exemple, on en trouvera 22).

Solution

Pour compter de 5 en 5 dans une suite d’entiers consécutifs, il suffit de les indexer et de ne compter que les multiples de 5 dans l’énumération.

D’où le code :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

a=1914
b=2020
cpt = 0
j=0

for i in range(a, b+1):
    if j%5==0:
        cpt = cpt + 1
    j = j + 1

print(cpt)

12

22

• Ligne 6 : la variable i est factice, elle permet juste à la boucle for de s’exécuter.
• Lignes 4 et 9 : la variable j sert à énumérer les entiers parcourus.
• Ligne 8 : on compte de 5 en 5.

Exercice type : Somme alternée plus/moins¶

On se donne un entier positif n, par exemple, n = 7. On cherche à calculer la « somme »

\(\mathtt{1-2+3-4+5-\dots \pm n}\)

où on alterne tantôt une addition, tantôt une soustraction. Pour n = 7, la somme vaut

\(\mathtt{1-2+3-4+5-6+7}= 4\)

Ecrire un code qui calcule s à partir de n. On pourra vérifier que pour n valant 2030 la somme vaut -1015.

Solution

En examinant l’exemple donné, on comprend qu’on effectue une addition sur les entiers impairs et une soustraction sur les entiers pairs. Il suffit donc de parcourir tous les entiers i entre 1 et n et d’ajouter ou retrancher i à une variable accumulatrice s initialisée à 0 selon que l’entier courant i est impair ou pair :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

n=2030
s=0

for i in range(1, n+1):
    if i % 2 == 1:
        s = s + i
    else:
        s = s - i

print(s)

11

-1015

On peut aussi donner une solution plus matheuse en remarquant que la somme cherchée n’est autre que

\(\displaystyle\sum_{i=1}^n (-1)^{i+1}i\)

ce qui donne le code suivant :

n=2030
s=0

for i in range(1, n+1):
    s = s - i*(-1)**i

print(s)

-1015

Exercice type : Afficher des nombres par paires¶

On se donne deux entiers \(a\) et \(b\), avec \(a\leq b\). Soit \(S\) la succession de tous les entiers depuis l’entier \(a\) inclus jusqu’à l’entier \(b\) inclus. On demande d’afficher tous les entiers de \(S\) par lignes de deux entiers consécutifs, sauf, éventuellement, la dernière ligne qui ne contiendra que le dernier élément de \(S\). Le tableau ci-dessous donne quatre exemples :

2 3
4 5
6 7
8 9

2 3
4 5
6 7
8

2

2 3

Bien tester tous ces cas.

Solution

On compte entre \(a\) et \(b\) un nombre de \(N=b-a+1\) entiers. Puisque les entiers doivent groupés par deux il y a aura \(q=N//2\) lignes de deux entiers et éventuellement une ligne de plus. Tout dépend de la parité de \(N\). L’idée est donc d’afficher les \(q\) premières lignes et selon les cas de rajouter une ligne. D’où le code suivant :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

a=2
b=9
N=b+1-a
q=N//2
x=a

for i in range(q):
    print(x, x+1)
    x=x+2
if N%2==1:
    print(b)

12
13
14
15

2 3
4 5
6 7
8 9

• Lignes 5 et 9 : x est le nombre qui est affiché en chaque début de ligne (sauf peut-être la dernière).
• Ligne 9 : en effet, les nombres vont deux par deux.
• Lignes 11-12 : s’il y a un nombre impair de nombres à afficher, c’est que le dernier est seul sur sa ligne, et le dernier entier à afficher est b.

Le code ci-dessus ne montre qu’un seul exemple, pour en voir d’autres, changer les valeurs de a ou b et exécuter à nouveau le code.

On peut simplifier le code de la manière suivante :

1
2
3
4
5
6
7
8

a=2
b=6

for i in range((b+1-a)//2):
    print(a, a+1)
    a=a+2
if a-1!=b:
    print(b)

 9
10
11

2 3
4 5
6

• La variable x du précédent code n’est pas indispensable, il suffit d’utiliser a mais la valeur initiale de a est alors perdue à la fin du programme.
• Une fois que les lignes contenant deux entiers sont affichés (lignes 4-6) on regarde si le dernier entier affiché est b. Si c’est la cas, tous les entiers ont été affiché et il n’y a rien de plus à afficher. Si ce n’est pas le cas, il faut afficher b (ligne 8). Quel est le dernier nombre affiché ? réponse : c’est a - 2 + 1 et donc a - 1, d’où la ligne 7.

Il était également possible de ne pas diviser par deux le nombre d’entiers à afficher :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

a=2
b=8
cpt=0

for i in range(a,b+1):
    cpt+=1
    if cpt ==2:
        print(i-1, i)
        cpt=0

if cpt !=0:
    print(b)

13
14
15
16

2 3
4 5
6 7
8

Le principe de ce code est de compter les nombres par groupes de 2 à l’aide du compteur cpt et lorsque le compteur atteint 2, les nombres sont affichés (ligne 8) et le compteur est remis à zéro (ligne 9).

Répéter 2030¶

Afficher les uns en dessous des autres 10 fois de suite l’entier 2030.

Afficher des entiers consécutifs¶

Afficher les uns en dessous des autres tous les entiers consécutifs entre 2020 et 2038.

Afficher deux listes l’une après l’autre¶

Écrire un code, utilisant deux boucles for successives qui produise l’affichage exact suivant (noter qu’il y a deux lignes dans le même affichage) :

42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61
65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84

Itérer 2x+1¶

On considère la suite de nombres entiers dont les premiers termes sont :

10, 21, 43, 87, 175, 351, etc

Cette suite est construite de la manière suivante :

• son premier terme est 10
• si \(x\) est un terme de la suite, le terme suivant vaut \(2x+1\).

Par exemple, si \(x=87\) alors le terme suivant dans la suite est \(2x+1=2\times 87 +1=175\).

Ecrire un code qui à partir d’un entier \(n>0\) affiche le \(n^{\text{e}}\) terme de la suite. Exemple de comportements selon la valeur de n :

3 -> 43
1 -> 10
7 -> 703

Somme des \(n\) premiers entiers¶

On se donne un entier \(n\geq 0\). Calculer la somme \(1+2+...+n\). Vérifier sur quelques exemples, que le résultat obtenu est bien \(\displaystyle\frac{n(n+1)}2\).

Somme de \(n\) entiers consécutifs¶

On se donne un entier \(\mathtt{n\geq 0}\) et on demande de calculer la somme de tous les entiers entre \(\mathtt{n}\) et \(\mathtt{2n}\). Par exemple, si \(\mathtt{n=5}\) alors la somme vaut

\(5+6+7+8+9+10=45\)

Somme d’entiers impairs consécutifs¶

On donne un entier \(N\geq 0\) et on demande de calculer la somme des \(N\) premiers entiers impairs, c’est-à-dire

\(1, 3, 5, 7, 9, 11, \text{etc}\)

Par exemple, si \(N=6\), on trouvera \(1+3+5+7+9+11=36\).

Vérifier dans vos tests que cette somme vaut toujours \(N^2\).

Sommes de puissances consécutives¶

On se donne un entier \(n\geq 0\). Calculer la somme \(1+10+...+10^{n-1}\). Par exemple, si \(n=5\), on obtiendra \(11111\) pour somme. Vérifier que vous obtenez bien \(\frac{10^{n}-1}9\).

Sommes de puissances de 2 ou de 3¶

On donne un entier \(\mathtt{n>0}\) et on demande de calculer la somme suivante :

\(S_n=3^1+2^2+3^3+2^ 4+\dots+ ?^n\)

Si l’exposant courant \(k\) est pair, on ajoute \(2^k\) sinon on ajoute \(3^k\). La somme s’arrête lorsqu’elle contient \(n\) termes. Par exemple, \(S_4=3^1+2^2+3^3+2^4=3 + 4 + 27 + 16=50\) et \(S_5=3^1+2^2+3^3+2^4+3^5=50+243=293\)

Somme alternée plus/moins en décroissant¶

On cherche à écrire un code capable de calculer des expressions du genre

\(\quad\quad\quad\quad\quad 7-6+5-4+3-2+1.\)

Plus précisément, on se donne un entier \(n>0\) (ci-dessus, c’était \(n=7\)) et on demande d’écrire un code qui renvoie la valeur de l’expression :

\(\quad\quad\quad\quad\quad\quad\quad n - (n-1) + (n-2) - (n-3) + \dots\)

expression qui se poursuit jusqu’à ce que le terme courant vaille 1. Noter que l’expression commence par \(n\) et alterne soustraction et addition. Si \(n=2037\) ou \(n=2038\) on trouvera que la somme vaut 1019.

Calcul d’une somme (sigma)¶

Calculer pour différentes valeurs de \(N\) la somme \(\displaystyle\sum_{n=1}^{N}\left(\frac 1{2n} -\frac 1{n+1}+\frac 1{2(n+2)}\right)\). Vers quelle valeur semble se rapprocher la somme lorsque \(N\) augmente ?

Plus grand diviseur impair¶

Soit un entier \(n>0\). On cherche le plus grand diviseur impair \(d\) de \(n\). Par exemple :

• si \(n=42\) alors \(d=21\),
• si \(n=45\) alors \(d=45\),
• si \(n=64\) alors \(d=1\),
• si \(n=1000\) alors \(d=125\).

Déterminer \(d\) est parcourant tous les entiers entre \(1\) et \(n\). En particulier, déterminer le plus grand diviseur impair de \(n=416241604\).

Compter de 0,5 en 0,5¶

Cet exercice est corrigé en vidéo.

On donne deux entiers \(a\) et \(b\) avec \(a\leq b\) et on demande d’afficher tous les nombres entre \(a\) et \(b\) si on compte de 0,5 en 0,5. Par exemple si \(a=42\) et \(b=49\), il faut afficher les nombres suivants, de préférence sur une même ligne :

42 42.5 43 43.5 44 44.5 45 45.5 46 46.5 47 47.5 48 48.5 49

Il est attendu qu’un entier soit affiché sans point décimal, par exemple 42 et pas 42.0

Compter par tiers¶

On donne deux entiers \(\mathtt{a}\) et \(\mathtt{b}\) avec \(\mathtt{a\leq b}\). On demande d’afficher le décompte entre \(\mathtt{a}\) et \(\mathtt{b}\) en progressant par tiers

Restes de deux entiers¶

Si on divise 1234567 par un certain nombre et on obtient 124 pour reste et si on divise 87654321 par le même nombre on trouve 760 pour reste. Trouver bestialement le nombre par lequel on a divisé.

Entier pyramidal¶

Un entier \(N>0\) est dit pyramidal si c’est le nombre de boules nécessaires pour bâtir une pyramide de hauteur \(n\) et de base un carré de côté ayant \(n\) boules, cf. l’image ci-dessous correspondant à \(n=5\) :

Pour la suite, on a juste besoin de savoir qu’un nombre pyramidal est de la forme

\(N= \frac {n(n+1)(2n+1)}6\)

Ainsi l’entier \(N=55\) est un nombre pyramidal car si \(n=5\) alors \(N= \frac {n(n+1)(2n+1)}6=55\). Les premiers nombres pyramidaux sont :

\(1, 5, 14, 30, 55, 91, 140.\)

Déterminer si les entiers suivants sont pyramidaux :

• \(N=1785\),
• \(N=2020\),
• \(N=4900\),
• \(N=317104004\),
• \(N=58963256321402313634\),
• \(N=30979120769004056775\)

On pourra utiliser que si \(N= \frac {n(n+1)(2n+1)}6\) alors \(n\leq 2\times N^{\frac 13}\)

Entiers oblongs¶

Un entier \(p>0\) est dit oblong (on dit aussi pronique) s’il peut s’écrire comme le produit de deux entiers consécutifs \(n\) et \(n+1\), autrement dit si \(p=n(n+1)\). Les nombres \(20=4\times 5\) ou \(42=6\times 7\) sont donc oblongs mais ce n’est pas le cas, par exemple, de

\(18 = 1\times 18 = 2\times 9 = 3\times 6\)

On demande de dire si les entiers suivants sont oblongs :

• \(p=4066272\),
• \(p=4088459\),
• \(p=7389121815995046018464320530\),
• \(p=5821012563999630124578500145\).

Il pourra être utile, dans les deux derniers cas, d’observer que si \(p=n(n+1)\) alors forcément \(n\leq \sqrt p\).

Produit d’entiers¶

Calculer le produit \(P\) des entiers entre 42 et 421, autrement dit \(P=42\times 43\times\cdots \times 420\times 421\).

On trouvera un très grand entier qui commence par 1484.

Allers et retours¶

On se donne deux entiers \(a\) et \(b\) avec \(a<b\) ainsi qu’un entier \(\mathtt{N>0}\). Un puce, placée initialement à l’entier \(a\), se déplace pendant \(\mathtt{N}\) secondes. A l’issue des \(\mathtt{N}\) secondes elle s’arrête à la position où elle se trouve. La puce se déplace entre l’entier \(a\) et l’entier \(b\geq a\) à raison d’une unité par seconde. Quand elle atteint \(b\) et que son parcours n’est pas fini, elle repart vers \(a\) et, de même, quand elle atteint \(a\) elle repart vers \(b\). On demande d’afficher seconde par seconde, toutes les étapes de son parcours lorsque son déplacement dure \(N\) secondes.

Par exemple, si \(a=5\), \(b=8\) et \(N=12\) alors l’affichage doit être :

0 seconde -> 5
1 secondes -> 6
2 secondes -> 7
3 secondes -> 8
4 secondes -> 7
5 secondes -> 6
6 secondes -> 5
7 secondes -> 6
8 secondes -> 7
9 secondes -> 8
10 secondes -> 7
11 secondes -> 6
12 secondes -> 5

On utilisera une variable x référençant la position courante de la puce et un drapeau appelé sens qui vaudra 1 si le déplacement courant se fait vers la droite et qui vaudra -1 si le déplacement courant se fait vers la gauche. Voici un template de code :

sens=1
N=12
a=5
b=8
x=a

print(0, "seconde ->", x)

for i in range(N):
    # Votre code

Pomodoro¶

Soit à afficher 10 fois l’heure à partir de 20h42 avec des intervalles d’attente de 25 minutes. On obtient alors l’affichage suivant :

20 h 42
21 h 7
21 h 32
21 h 57
22 h 22
22 h 47
23 h 12
23 h 37
0 h 2
0 h 27

Plus généralement, on donne un moment de la journée par

• son nombre d’heures h,
• son nombre de minutes m,

par exemple, h=20 et m =42 ;

on donne aussi

• une période de temps, en minutes, par exemple periode=25 en supposant que \(\mathtt{periode < 60}\)
• un nombre entier, disons \(\mathtt{n\geq 1}\)

et on demande d’afficher l’heure qu’il est aux n moments à partir de l’heure donnée et à intervalles réguliers de periode minutes. Le nombre d’heures affiché doit toujours être strictement inférieur à 24 et le nombre de minutes strictement inférieur à 60.

Afficher par paires verticales¶

On donne deux entiers \(a\) et \(b\) et on demande d’afficher, par ordre croissant tous les entiers de \(a\) à \(b\) sur deux lignes en plaçant alternativement les entiers sur la ligne du haut et sur la ligne du bas. Par exemple, si \(a=2018\) et \(b=2025\) le code doit afficher

2018 2020 2022 2024
2019 2021 2023 2025

et si \(a=2020\) et \(b=2038\) le code doit afficher

2020 2022 2024 2026 2028 2030 2032 2034 2036 2038
2021 2023 2025 2027 2029 2031 2033 2035 2037

Afficher par triplets verticaux¶

On donne deux entiers \(a\) et \(b\) et on demande d’afficher, par ordre croissant tous les entiers de \(a\) à \(b\) sur trois lignes en plaçant successivement les entiers sur la ligne du haut, la ligne centrale et sur la ligne du bas. Par exemple, si \(a=42\) et \(b=53\) le code doit afficher

42 45 48 51
43 46 49 52
44 47 50 53

et si \(a=2019\) et \(b=2038\) le code doit afficher

2019 2022 2025 2028 2031 2034 2037
2020 2023 2026 2029 2032 2035 2038
2021 2024 2027 2030 2033 2036

Suite de disques¶

On se donne des entiers \(n, R, s>0\), par exemple \(n=8\), \(R=2.5\) et \(s=1\). Dessiner un alignement horizontal de \(n\) disques noirs de rayon \(R\), deux disques successifs étant séparés par une distance de \(s\).

Carrés côte-à-côte¶

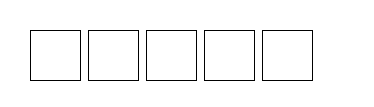
On donne un entier \(\mathtt{n\geq 0}\), un entier \(\mathtt{c>0}\) et un entier \(\mathtt{sep > 0}\). Construire une suite de \(\mathtt{n}\) carrés, alignés horizontalement, de côté \(\mathtt{c}\) et séparés d’une longueur \(\mathtt{sep}\).

Par exemple, si \(\mathtt{n = 5}\), \(\mathtt{sep = 8}\) et \(\mathtt{c = 50}\) alors le code affichera :

Dents de scie¶

Dessiner une ligne polygonale formée de \(\mathtt{n}\) dents de scie. La hauteur de chaque dent sera enregistrée dans une variable \(\mathtt{h}\) et la largeur dans une variable \(\mathtt{L}\). Le dessin ci-dessous correspond à \(\mathtt{n=5}\), \(\mathtt{h=100}\) et \(\mathtt{L=40}\).

Cible¶

On se donne un entier \(n>0\) par exemple \(n=10\). Dessiner une cible bicolore noire et jaune constituée de \(n\) disques :

le disque central de la cible sera indifféremment jaune ou noir et les couronnes seront de largeur constante. Aucune contrainte n’est imposée sur la valeur du rayon du disque central. La couronne extérieure sera noire.

Indications : on dessinera des disques en commençant par celui de plus grand rayon. Pour gérer l’alternance des couleurs, on prendra en compte la parité du compteur de boucle.

[Exercice fourni par mon collègue P. Piccinini.]

Dessiner un U¶

Dessiner le motif ci-dessous. Chaque disque est tangent à son ou ses voisins. Chaque côté contient le même nombre \(n\) de disques, dans l’exemple \(n=5\). Le rayon de chaque disque sera de 20.

Disques en carrés¶

1. Dessiner une suite de disques de diamètre d donné qui forment un carré ayant \(n\) disques par côté où \(n\) est donné.

   

2. Refaire le même dessin mais en alternant les couleurs orange et bleue.

   

Collier de perles¶

Dessiner un collier monocolore :

puis un collier bicolore :

Le collier aura la forme d’un cercle de rayon \(R\). Si le collier a \(n\) perles, chaque perle sera un disque de centre \((R\cos(2k\pi/n), R\sin(2k\pi/n))\) où \(k\) prendra \(n\) valeurs entières à partir de \(0\). L’observation attentive du dessin vous fera comprendre comment déterminer la dimension de chaque perle. Le dessin ci-dessus a été effectué avec 50 perles de couleur orange ou bleu (si le collier est bicolore, \(n\) est pair).

Carrés concentriques¶

Écrire un programme qui dessine \(n\) carrés concentriques, centrés en l’origine, avec un écart de \(e\) entre deux carrés successifs. Utiliser une variable pour paramétrer la longueur du côté du carré initial.

Dessiner un faisceau de demi-droites¶

Dessiner le motif ci-dessous.

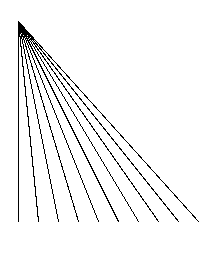
Plus précisément, on demande de construire \(n\) segments dont une extrémité est le point \((0,0)\) et les autres extrémités étant placées

• sur une base horizontale située à une distance d de \((0,0)\) et située en-dessous de \((0,0)\)
• régulièrement espacées (espacement régulier valant delta)

Le segment le plus à gauche sera vertical. Sur la figure, n=10, d=200 et delta=20.

Clôturer un champ carré¶

On veut graphiquement clôturer un champ carré de côté \(a\) :

La distance entre deux poteaux est constante et vaut \(25\). Chaque coin du champ comporte un poteau.

Dessiner le champ ainsi que tous les poteaux de la clôture. Le côté \(a\) du champ pourra être un quelconque multiple de 25 ; le dessin a été réalisé pour \(a=300\).

Grille carrée¶

Dessiner une grille carrée comme ci-dessous :

La largeur de chaque case sera enregistrée dans une variable \(\mathtt{c}\) et le nombre de cases par côté dans une variable \(\mathtt{n}\). On dessinera la grille non pas case par case mais comme on le ferait à la main : on trace d’abord \(\mathtt{n + 1}\) lignes verticales que l’on croise ensuite avec \(\mathtt{n + 1}\) lignes horizontales.

Grille de Sudoku¶

Dessiner une grille de sudoku comme ci-dessous :

Pyramide maya¶

On demande de dessiner une pyramide telle que celle ci-dessous :

On utilisera des variables:

• n : le nombre de marches
• h : la hauteur de chaque marche
• p : la profondeur de chaque marche
• L : la longueur commune des autres traits.