Programmation en Numba sur le GPU¶
Modèle de programmation Cuda¶
La vidéo High-Performance Computing with Python: Numba and GPUs de juillet 2019 fournit une introduction pédagogique à la programmation GPU qu’il pourra être bénéfique de regarder avant d’entrer dans les détails du modèle de programmation CUDA.
Le jargon a imposé les termes suivants que j’utiliserai parfois :
- device ie périphérique au lieu de GPU
- host ie hôte pour le CPU.
Cela est dû au fait qu’il y a des échanges entre le CPU et le GPU.
Un thread sur GPU est un flot d’instructions exécutées par un cœur GPU, un cœur pouvant exécuter, par exemple, 10 threads. Les threads vont exécuter en parallèle un même kernel, un kernel étant une simple fonction que l’utilisateur écrit à partir des besoins de son programme.
Description¶
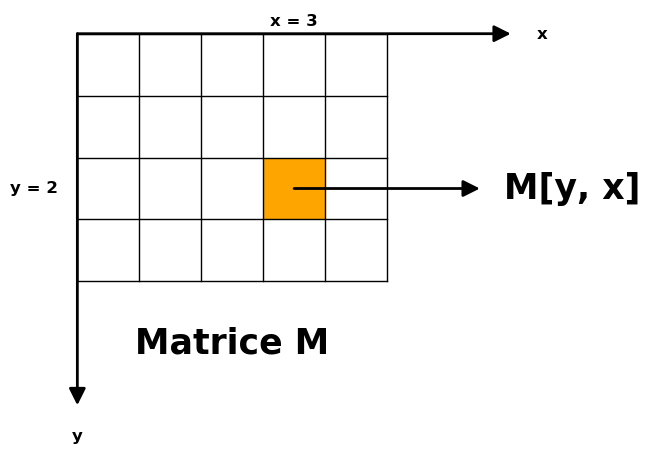
Dans le modèle de programmation Cuda, les threads sont réprésentés par une grille constituée de blocs de threads. La grille et les blocs sont de même dimension \(\mathtt{d}\) où \(\mathtt{d}\) est parmi 1, 2 ou 3. Le principe de tout ce qui va être expliqué ci-dessous est le même pour chacune des dimensions \(\mathtt{d}\). Puisque les deux exemples qui seront présentés dans ce document calculeront sur le GPU des coefficients d’une matrice, il sera plus commode de choisir \(\mathtt{d=2}\) mais \(\mathtt{d=1}\) ou \(\mathtt{d=3}\) pourrait s’adapter à nos exemples.
Dans le cas de la dimension 2, attention que l’ordre habituel \(\mathtt{(ligne, colonne)}\) dans lequel on se représente un tableau 2D se traduit par (ordonnée, abscisse) :
- une coordonnées en largeur est souvent notée en utilisant la lettre \(\mathtt{x}\) ; une largeur correspond à un écart de colonnes
- une coordonnées en hauteur est souvent notée en utilisant la lettre \(\mathtt{y}\) ; une hauteur correspond à un écart de lignes.
Entrons dans le détail :
La grille est constituée de blocs à deux dimensions, \(\mathtt{nbx}\) blocs en largeur, \(\mathtt{nby}\) blocs en hauteur
Chaque bloc de la grille est identifié par les deux indices
- l’indice \(\mathtt{bx}\) de colonne dans la grille avec \(\mathtt{0\leq bx< nbx}\),
- l’indice \(\mathtt{by}\) de ligne dans la grille avec \(\mathtt{0\leq by< nby}\).
Chaque bloc est constitué de threads.
Chaque bloc a deux dimensions \(\mathtt{ntx}\) et \(\mathtt{nty}\) et tous les blocs de la grille ont mêmes dimensions
Chaque thread d’un bloc est référencé avec deux indices \(\mathtt{tx}\) et \(\mathtt{ty}\) où \(\mathtt{0\leq tx< ntx}\) et où \(\mathtt{0\leq ty< nty}\)
Chaque bloc contient donc le même nombre de threads à savoir \(\mathtt{ntx \times nty}\).
Le nombre de threads par bloc est matériellement limité, par exemple à 1024 ; on peut donc envisager des blocs de 32 x 32 threads.
Si on voit la grille comme une grille de threads (et non de blocs) chaque thread a deux indices absolus :
- l’indice de colonne : \(\mathtt{x = bx \times ntx + tx}\),
- l’indice de ligne : \(\mathtt{y = by \times nty + ty}\).
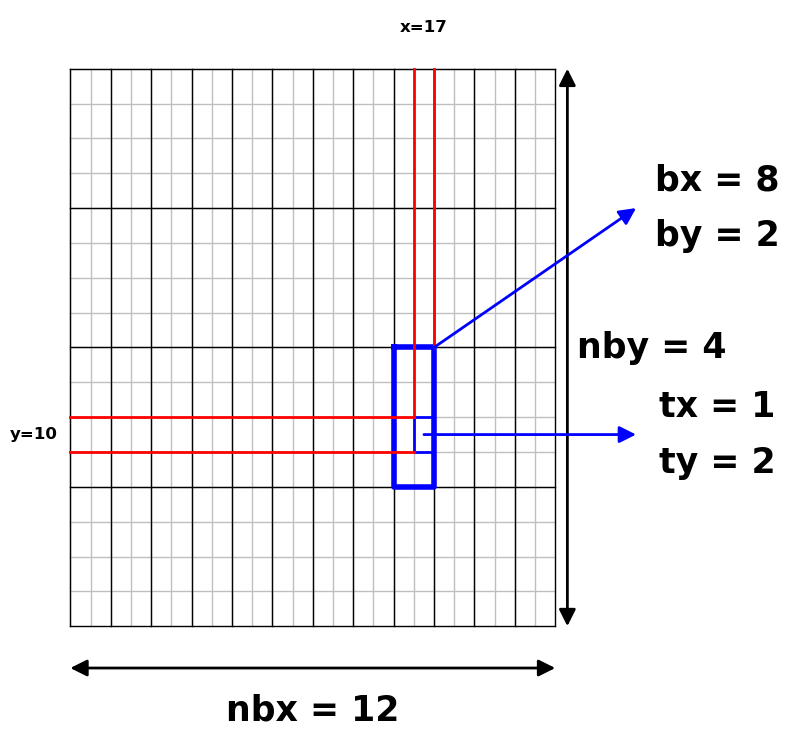
Dans le dessin ci-dessus, on a une grille de \(\mathtt{nbx \times nby = 12 \times 4}\) blocs. Chaque bloc se décompose en \(\mathtt{ntx \times nty = 2 \times 4}\) threads. On a isolé, en bleu, dans le bloc (bx, by) = (8, 2) le thread (tx, ty) = (1, 2). La position absolue de ce thread est (x, y) = (17, 10).
Utlisation du modèle pour le calcul matriciel¶
Imaginons qu’on veuille effectuer le produit matriciel \(\mathtt{A\times B =: C}\) où
- \(\mathtt{A}\) est une matrice de taille lignes x colonnes \(\mathtt{(n, p)}\),
- \(\mathtt{B}\) est une matrice de taille lignes x colonnes \(\mathtt{(p, q)}\),
- \(\mathtt{C}\) est donc une matrice de taille lignes x colonnes \(\mathtt{(n, q)}\).
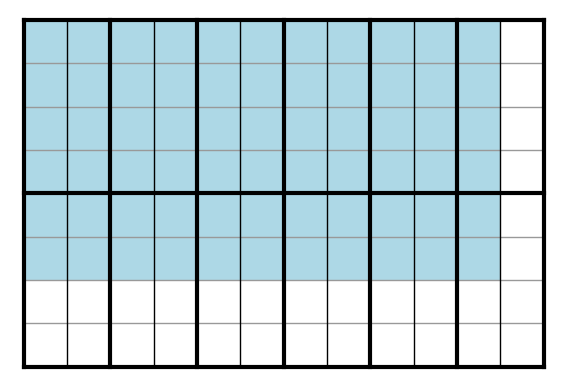
Pour fixer les idées, cf. figure ci-dessous où la matrice C est en bleu, on va supposer que
\(\mathtt{n=6}\), \(\mathtt{p=8}\), \(\mathtt{q=11}\)
en sorte que \(\mathtt{C}\) est de largeur 11 et de hauteur 6. Dans le modèle, on recouvre la matrice \(\mathtt{C}\) à calculer par une grille de blocs de threads. Pour fixer les idées, on va choisir chaque bloc de taille dimt= (2, 4) donc chaque bloc contient \(\mathtt{2\times 4=8}\) threads :
On posera \(\mathtt{ntx=2}\) et \(\mathtt{nty=4}\). Calculons le nombres de blocs en largeur et en hauteur pour recouvrir la matrice \(\mathtt{C}\) :
- chaque bloc à une largeur de \(\mathtt{ntx=2}\) et \(\mathtt{q=11}\) donc il faut en largeur \(\mathtt{nbx=6}\) blocs (et il y aura \(\mathtt{6\times 2 -11=1}\) thread inutile en largeur) ;
- chaque bloc à une hauteur de \(\mathtt{nty=4}\) et \(\mathtt{n=6}\) donc il faut en hauteur \(\mathtt{nby=2}\) blocs (et il y aura \(\mathtt{4\times 2 -6=2}\) threads inutiles en hauteur).
Comme on le voit sur la figure, la grille est formée de \(\mathtt{2 \times 6}\) blocs.
La grille ainsi constituée a une largeur de 12 threads et une hauteur de 8 threads et donc peut exécuter 96 threads, ce qui excède le nombre total des 66 coefficients de C à calculer.
Initialement, les matrices \(\mathtt{A}\) et \(\mathtt{B}\) ainsi qu’une matrice \(\mathtt{C}\) nulle et à la bonne taille sont définies sur l’hôte. Ces matrices sont envoyées sur le device. Pour calculer la matrice \(\mathtt{C}\), il y aura au moins autant de threads sur le GPU que de coefficients de \(\mathtt{C}\) à calculer. Dans notre exemple, il y aura 96 threads indexés \(\mathtt{(x, y)}\) avec \(\mathtt{0\leq x< 12}\) et \(\mathtt{0\leq y< 8}\).
Quand on lance un kernel, cf. les exemples de code plus bas, outre les données utiles au calcul, ici \(\mathtt{A}\), \(\mathtt{B}\) et \(\mathtt{C}\), on lui donne le couple \(\mathtt{dimb=(nbx, nby)}\) et le couple \(\mathtt{dimt=(ntx, nty)}\). Par ailleurs, quand ce kernel s’exécute, il sait dans quel bloc \(\mathtt{(bx, by)}\) de la grille il s’exécute et quel thread \(\mathtt{(tx, ty)}\) du bloc il exécute. Cela lui permet de savoir dans quel thread \(\mathtt{(x, y)}\) de la grille il s’exécute. Et notre kernel va être écrit en sorte que l’élément en colonne \(\mathtt{x}\) et ligne \(\mathtt{y}\) soit représenté par le thread indexé \(\mathtt{(x, y)}\).
En pratique, il est fréquent que les blocs de threads soient « carrés », ie que \(\mathtt{ntx=nty}\).
Références¶
Le modèle de programmation Cuda est décrit en détail dans un document officiel : Cuda programming model.
Plus généralement, concernant la programmation Cuda, on pourra consulter l’ouvrage progressif et détaillé CUDA C Programming paru en 2014.
Illustration par le produit matriciel¶
Le modèle de programmation Cuda étant décrit, nous disposons de tous les éléments pour comprendre comment on met en œuvre un produit matriciel basique sur GPU. Les matrices sont représentées par des tableaux Numpy. Voici un tel programme :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 | import numpy as np
from numba import cuda
@cuda.jit('(int64[:,:], int64[:,:], int64[:,:])')
def cu_square_matrix_mul(A, B, C):
n, p=A.shape
_, q=B.shape
x, y = cuda.grid(2)
if x >= q or y >= n:
return
for i in range(p):
C[y, x] += A[y, i] * B[i, x]
def make_data(n, p, q, bound):
A = np.random.randint(low=-bound, high=bound+1,
size=(n, p), dtype=np.int64)
B = np.random.randint(low=-bound, high=bound+1,
size=(p, q), dtype=np.int64)
C = np.zeros((n, q), dtype=np.int64)
return A, B, C
def dims(n, q, nt):
ntx, nty = nt
# nb colonnes de blocs
nbx=q//ntx+(q%ntx)
# nb lignes de blocs
nby=n//nty+(n%nty)
return (nbx, nby)
def cuda_mult(A, B, C, nb, nt):
dA = cuda.to_device(A)
dB = cuda.to_device(B)
dC = cuda.to_device(C)
cu_square_matrix_mul[nb, nt](dA, dB, dC)
cuda.synchronize()
dC.to_host()
def main():
bound=10
n=6
p=8
q=11
A, B, C=make_data(n, p, q, bound)
dimtx=2
dimty=4
dimt=(dimtx, dimty)
dimb = dims(n, q, dimt)
cuda_mult(A, B, C, dimb, dimt)
print((C))
print()
print(A@B)
main()
|
[[ 64 -84 132 -34 -12 -8 64 -261 97 -3 -82]
[-188 -71 -37 87 -200 169 -152 23 142 -83 148]
[ 2 -35 142 -26 15 -89 -41 -109 -66 -83 -60]
[ 202 13 44 -18 126 -72 157 -249 82 102 -111]
[ -44 -15 -35 59 86 -3 33 -3 -23 31 54]
[ 252 63 -73 49 -67 76 65 -167 0 -71 147]]
[[ 64 -84 132 -34 -12 -8 64 -261 97 -3 -82]
[-188 -71 -37 87 -200 169 -152 23 142 -83 148]
[ 2 -35 142 -26 15 -89 -41 -109 -66 -83 -60]
[ 202 13 44 -18 126 -72 157 -249 82 102 -111]
[ -44 -15 -35 59 86 -3 33 -3 -23 31 54]
[ 252 63 -73 49 -67 76 65 -167 0 -71 147]]
La sortie montre le calcul du produit matriciel d’abord effectué par Cuda et d’autre part, effectué par Numpy. On observe que les résultats coïncident bien. On reprend l’exemple du produit \(\mathtt{C}\) d’une matrice A de taille \(\mathtt{(6, 8)}\) et d’une matrice B de taille \(\mathtt{(8, 11)}\).
Le kernel¶
Il est déclaré ligne 5. Il s’exécute sur le device. Il reçoit les matrices \(\mathtt{A}\), \(\mathtt{B}\) et \(\mathtt{C}\) qui se trouvent sur le device. La fonction est décorée ligne 4 par le décorateur cuda.jit. C’est ce décorateur qui indique à Numba que la fonction est un kernel. On passe à ce décorateur, sous forme de chaîne de caractères, ici
'(int64[:,:], int64[:,:], int64[:,:])'
un triplet de types de données transmises au kernel. Ici int64[:,:] désigne un tableau 2d d’entiers sur 64 bits. On trouvera quelques indications sur des signatures courantes ici : signature specifications.
Les kernels s’exécutent en parallèle. Chaque kernel calcule à la ligne 16 le coefficient de \(\mathtt{C}\) à la ligne \(\mathtt{y}\) et à la colonne \(\mathtt{x}\) de la grille. Ce calcul résulte tout simplement du produit ligne par colonne, effectué dans le kernel par la boucle for de la ligne 15.
Le code ci-dessus ne le montre pas, mais le kernel quand il s’exécute, connait le bloc et le thread d’exécution ; par ailleurs, suite à l’appel ligne 43, le kernel dispose des dimensions de chaque bloc (le dimt) et des dimensions de la grille en blocs (le dimb). Donc, à l’aide d’une formule assez simple, le kernel est en mesure de calculer la position absolue \(\mathtt{(x, y)}\) du thread dans la grille. Pour nous épargner le calcul, Numba met à disposition ligne 10 une fonction cuda.grid qui calcule cette position. Il faut donner à cette fonction la dimension des blocs, dans notre exemple, ce sont les 2 dimensions (le \(\mathtt{d=2}\) expliqué dans la description du modèle Cuda) mais on avait vu en introduction du modèle de programmation Cuda qu’il serait possible de choisir des dimensions 1 ou 3.
On a vu que la grille de threads déborde de la matrice \(\mathtt{C}\). Donc, le kernel doit d’assurer (cf. ligne 12) que le calcul effectué en \(\mathtt{(x, y)}\) correspond à une position légitime de la matrice \(\mathtt{C}\).
Un kernel ne renvoie rien, il agit par effet de bord.
Dimensions de la grille¶
Le nombre de threads qu’un bloc peut exécuter est plafonné. Par exemple, pour la carte graphique que j’ai utilisée, il est de 1024. Dans ce cas et si les blocs sont de dimension 2, il est courant de choisir un bloc de taille \(\mathtt{32\times 32}\). Dans notre petit exemple, on a choisi une taille \(\mathtt{(2, 4)}\), cf. lignes 56-57. Quand on connait les dimensions de chaque blocs, il est facile de calculer le nombre de blocs suivant chaque dimension pour recouvrir la matrice. C’est ce que fait la fonction dims(n, q, nt). L’idée du calcul par les formules lignes 30 et 33 a été donné lors de la description de l’exemple où on avait trouvé une grille de dimension de \(\mathtt{(2, 6)}\). Plus loin dans ce document, un aparté explique comment trouver cette formule et lui donner la forme habituellement rencontrée.
Calcul du produit matriciel¶
Les étapes sont les suivantes :
- lignes 19-20 et 21-22 : sur le host, on génère aléatoirement des matrices Numpy \(\mathtt{A}\) et \(\mathtt{B}\) à coefficients entre -10 et 10 et de type
int64ainsi qu’une matrice Numpy \(\mathtt{C}\) initialisée à 0 - lignes 39-41 : on déplace les 3 matrices sur le device ; Numba se charge pour nous de l’allocation mémoire et du transfert.
- ligne 43 : on lance le kernel en donnant tous les éléments utiles : les 3 matrices, bien sûr, et aussi, entre crochets, les dimensions de chaque bloc et de la grille.
- ligne 44 : la synchronisation va avoir pour effet que l’hôte va interrompre son fil d’exécution jusqu’à ce que tous les threads exécutant le kernel aient terminé.
- ligne 46 : copie la matrice depuis le device vers le host.
- lignes 63 et 65 : on peut alors accéder au résultat et par exemple comparer.
Variante d’écriture du kernel¶
Le kernel écrit dans le programme ci-dessus :
@cuda.jit('(int64[:,:], int64[:,:], int64[:,:])')
def cu_square_matrix_mul(A, B, C):
n, p=A.shape
_, q=B.shape
x, y = cuda.grid(2)
if x >= q or y >= n:
return
for i in range(p):
C[y, x] += A[y, i] * B[i, x]
est parfois écrit de manière moins directe. En effet, Numba met à notre disposition la fonction cuda.grid mais il est possible de calculer explicitement \(\mathtt{x}\) et \(\mathtt{y}\). D’où le code suivant :
@cuda.jit('(int64[:,:], int64[:,:], int64[:,:])')
def cu_square_matrix_mul(A, B, C):
n, p=A.shape
_, q=B.shape
tx = cuda.threadIdx.x
ty = cuda.threadIdx.y
bx = cuda.blockIdx.x
by = cuda.blockIdx.y
bw = cuda.blockDim.x
bh = cuda.blockDim.y
x = tx + bx * bw
y = ty + by * bh
if x >= q or y >= n:
return
for i in range(p):
C[y, x] += A[y, i] * B[i, x]
En effet, chaque thread connait la position de son bloc dans la grille. On y a accède de la manière suivante :
bx = cuda.blockIdx.x
by = cuda.blockIdx.y
Il en est de même pour le thread dans son bloc :
tx = cuda.threadIdx.x
ty = cuda.threadIdx.y
Le thread connaît aussi la dimension nb de chaque bloc car il lui a été fournie entre crochets au moment du lancement du kernel :
cu_square_matrix_mul[nb, nt](dA, dB, dC)
Depuis le kernel, on y accède de la manière suivante :
bw = cuda.blockDim.x
bh = cuda.blockDim.y
autrement dit, on a nb = (bw, bh).
À partir de là, et vue la structure de la grille
on en déduit que
x = tx + bx * bw
y = ty + by * bh
Produit matriciel : performances¶
Il est temps de regarder combien notre calcul de produit de matrices sur GPU améliore ce que Python nous propose par défaut, à savoir la multiplication de Numpy. Pour cela on va calculer le produit de deux matrices carrées de taille 2500 :
from time import time
import numpy as np
from numba import cuda, int64
@cuda.jit('(int64[:,:], int64[:,:], int64[:,:])')
def kernel_mat_mult(A, B, C):
n, p=A.shape
q=B.shape[1]
x, y = cuda.grid(2)
if x >= q or y >= n:
return
for i in range(p):
C[y, x] += A[y, i] * B[i, x]
def make_data(n, p, q, bound):
A = np.random.randint(low=-bound, high=bound+1,
size=(n, p), dtype=np.int64)
B = np.random.randint(low=-bound, high=bound+1,
size=(p, q), dtype=np.int64)
C = np.zeros((n, q), dtype=np.int64)
return A, B, C
def dims(n, q, nt):
ntx, nty = nt
# nb colonnes de blocs
nbx=q//ntx+(q%ntx)
# nb lignes de blocs
nby=n//nty+(n%nty)
return (nbx, nby)
def cuda_mult(A, B, C, nb, nt):
dA = cuda.to_device(A)
dB = cuda.to_device(B)
dC = cuda.to_device(C)
kernel_mat_mult[nb, nt](dA, dB, dC)
cuda.synchronize()
dC.to_host()
def host_mult(A, B):
return A @ B
def main():
bound=10
n=p=q=2500
dstart = time()
A, B, C=make_data(n, p, q, bound)
dend = time()
tcuda = dend - dstart
print('Data: %.2fs' %tcuda)
dimtx=32
dimty=32
dimt=(dimtx, dimty)
dimb = dims(n, q, dimt)
dstart = time()
cuda_mult(A, B, C, dimb, dimt)
dend = time()
tcuda = dend - dstart
print('Cuda: %.2fs' % tcuda)
hstart = time()
P=host_mult(A, B)
hend = time()
thost = hend - hstart
print('Numpy: %.2fs' % thost)
print("Check:", np.array_equal(P, C))
main()
Data: 0.13s
Cuda: 0.63s
Numpy: 27.47s
Check: True
L’amélioration est d’un facteur de l’ordre de 40. Noter toutefois que le temps de Numpy n’est pas un bon temps de référence, étant très lent pour des matrices à coefficients entiers. Un code écrit en C++ en utilisant des vecteurs de la STL met environ 9s, ce qui donne finalement seulement une amélioration d’un facteur 15.
Activité du GPU pendant un calcul¶
Grâce à l’outil nvidia-smi, on peut visualiser l’état instantané du GPU (processeurs et mémoire). Voici par exemple son état pendant un gros calcul matriciel :
$ nvidia-smi
Tue Jul 28 15:11:00 2020
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 450.51.05 Driver Version: 450.51.05 CUDA Version: 11.0 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|===============================+======================+======================|
| 0 GeForce GTX 970 On | 00000000:01:00.0 Off | N/A |
| 78% 76C P2 118W / 173W | 3688MiB / 4041MiB | 100% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
(affichage partiel) où on voit l’occupation des threads et l’état de la mémoire. Ci-dessous, la suite de l’affichage avec l’occupation par processus, en particulier le processus python3 de la dernière ligne :
+-----------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=============================================================================|
| 0 N/A N/A 1038 G /usr/lib/xorg/Xorg 61MiB |
| 0 N/A N/A 1548 G /usr/lib/xorg/Xorg 128MiB |
| 0 N/A N/A 1749 G /usr/bin/gnome-shell 123MiB |
| 0 N/A N/A 3858 G nvidia-settings 3MiB |
| 0 N/A N/A 4031 C python3 3353MiB |
+-----------------------------------------------------------------------------+
Et voici, l’affichage une fois le calcul matriciel terminé :
po@po-20-04:~$ nvidia-smi
Tue Jul 28 15:11:12 2020
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 450.51.05 Driver Version: 450.51.05 CUDA Version: 11.0 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|===============================+======================+======================|
| 0 GeForce GTX 970 On | 00000000:01:00.0 Off | N/A |
| 78% 71C P0 81W / 173W | 332MiB / 4041MiB | 0% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=============================================================================|
| 0 N/A N/A 1038 G /usr/lib/xorg/Xorg 61MiB |
| 0 N/A N/A 1548 G /usr/lib/xorg/Xorg 128MiB |
| 0 N/A N/A 1749 G /usr/bin/gnome-shell 123MiB |
| 0 N/A N/A 3858 G nvidia-settings 3MiB |
+-----------------------------------------------------------------------------+
po@po-20-04:~$
Hélas, la vue fournie n’est qu’instantanée, il faut relancer nvidia-smi pour toute nouvelle vue.
Sous Linux, il existe une application graphique permettant de suivre l’occupation du GPU mais elle est compliquée à installer (il faut compiler les sources depuis Github).
Améliorer les performances en utilisant la mémoire partagée¶
Ci-dessous, nous allons calculer le produit de deux matrices carrées de grande taille, environ 10000. Plus précisément, on va choisir 10112 qui est le premier multiple de 32 au-dessus de 10000. Ne pas placer une matrice trop grande, vous pourriez avoir une erreur pour mémoire insuffisante :
CUDA_ERROR_OUT_OF_MEMORY
Le code Cuda de produit matriciel déjà écrit utilisait la mémoire globale du GPU. Voici son exécution pour \(\mathtt{n=10112}\)
from time import time
import numpy as np
from numba import cuda, int64
@cuda.jit('(int64[:,:], int64[:,:], int64[:,:])')
def kernel_mat_mult(A, B, C):
n, p=A.shape
q=B.shape[1]
x, y = cuda.grid(2)
if x >= q or y >= n:
return
for i in range(p):
C[y, x] += A[y, i] * B[i, x]
def make_data(n, p, q, bound):
A = np.random.randint(low=-bound, high=bound+1,
size=(n, p), dtype=np.int64)
B = np.random.randint(low=-bound, high=bound+1,
size=(p, q), dtype=np.int64)
C = np.zeros((n, q), dtype=np.int64)
return A, B, C
def dims(n, q, nt):
ntx, nty = nt
# nb colonnes de blocs
nbx=q//ntx+(q%ntx)
# nb lignes de blocs
nby=n//nty+(n%nty)
return (nbx, nby)
def cuda_mult(A, B, C, nb, nt):
dA = cuda.to_device(A)
dB = cuda.to_device(B)
dC = cuda.to_device(C)
kernel_mat_mult[nb, nt](dA, dB, dC)
cuda.synchronize()
dC.to_host()
def main():
bound=10
n=p=q=10112
dstart = time()
A, B, C=make_data(n, p, q, bound)
dend = time()
tcuda = dend - dstart
print('Data: %.2fs' %tcuda)
dimtx=32
dimty=32
dimt=(dimtx, dimty)
dimb = dims(n, q, dimt)
dstart = time()
cuda_mult(A, B, C, dimb, dimt)
dend = time()
tcuda = dend - dstart
print('GPU global: %.2fs' % tcuda)
main()
Data: 2.07s
GPU global: 37.89s
Le même programme exécuté sur Google Colab :
from numba import cuda
cuda.detect()
Found 1 CUDA devices
id 0 b'Tesla K80' [SUPPORTED]
compute capability: 3.7
pci device id: 4
pci bus id: 0
Summary:
1/1 devices are supported
True
affiche un temps de :
Data: 3.35s
GPU global: 46.11s
La documentation de Numba précise que la version présentée ci-dessus est peu performante car elle utilise la mémoire dite globale du GPU qui est lente. Elle suggère une implémentation plus rapide qui utilise la mémoire partagée (shared memory) du GPU. C’est une mémoire, un peu analogue au cache d’un CPU, en quantité limitée mais mais dont le temps d’accès est plus court que pour la mémoire globale. Elle est partagée par tous les threads du même bloc. Pour plus d’information sur la différence entre ces deux types de mémoire, on pourra consulter : why shared memory is faster than global memory?.
Le programme ci-dessous est un code simplifié de celui donné en exemple dans le code-source de Numba. Pour le produit de deux matrices de taille 10112, le temps est presque divisé par trois. Voici le code :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 | from time import time
import numpy as np
from numba import cuda, int64
BLOCK = 32
BOUND = 10
@cuda.jit('(int64[:,:], int64[:,:], int64[:,:])')
def kernel_mat_mult_shared(A, B, C):
sA = cuda.shared.array(shape=(BLOCK, BLOCK), dtype=int64)
sB = cuda.shared.array(shape=(BLOCK, BLOCK), dtype=int64)
n, _ = A.shape
bpg = n // BLOCK
x, y = cuda.grid(2)
tx = cuda.threadIdx.x
ty = cuda.threadIdx.y
acc = 0
for i in range(bpg):
sA[ty, tx] = A[y, tx + i * BLOCK]
sB[ty, tx] = B[ty + i * BLOCK, x]
cuda.syncthreads()
for j in range(BLOCK):
acc += sA[ty, j] * sB[j, tx]
cuda.syncthreads()
C[y, x] = acc
def make_data(bpg):
n = BLOCK * bpg
A = np.random.randint(low=-BOUND, high=BOUND + 1,
size=(n, n), dtype=np.int64)
B = np.random.randint(low=-BOUND, high=BOUND + 1,
size=(n, n), dtype=np.int64)
C = np.empty_like(A)
return A, B, C
def mat_mult_shared(A, B, C, bpg):
dA = cuda.to_device(A)
dB = cuda.to_device(B)
dC = cuda.to_device(C)
kernel_mat_mult_shared[(bpg, bpg), (BLOCK, BLOCK)](dA, dB, dC)
cuda.synchronize()
dC.to_host()
return C
def go(bpg):
n = bpg * BLOCK
start = time()
A, B, C = make_data(bpg)
end = time()
print("Dataset : %.2fs" % (end - start))
dstart = time()
mat_mult_shared(A, B, C, bpg)
dend = time()
print("GPU shared : %.2fs" % (dend - dstart))
A=np.array(A, dtype=np.float64)
B=np.array(B, dtype=np.float64)
dstart = time()
D = A@B
dend = time()
print("Numpy : %.2fs" % (dend - dstart))
D=np.array(D, dtype=np.int64)
print(np.array_equal(C, D))
bpg = 316
n = BLOCK * bpg
print("n =", n)
go(bpg)
|
qui affiche
n = 10112
Dataset : 2.07s
GPU shared : 13.06s
Numpy : 12.11s
True
Deux observations concernant le temps d’exécution :
- l’utilisation de la mémoire partagée a divisé le temps d’exécution par presque 3 ;
- Numpy a réussi à calculer le produit ! mais en passant par un calcul en flottant et le temps est encore meilleur que le temps sur GPU avec mémoire partagé (cette performance remarquable avait été évoquée en 2e partie du document).
Sur le même GPU de Google Colab que ci-dessus, le temps d’exécution est :
n = 10112
Dataset : 2.72s
GPU shared : 14.54s
Numpy : 57.97s
True
Le ratio pour le GPU est à peu près le même, en revanche, le temps d’exécution de Numpy n’est pas du tout dans le même rapport (il est possible qu’il ne soit exécuté que sur un seul thread).
Décrivons le code Numba ci-dessus. La matrice \(\mathtt{C=A\times B}\) est découpée est blocs de \(\mathtt{32\times 32}\), dans le code ci-dessus, BLOCK=32. Il y a \(\mathtt{bpg=316}\) blocs (bpg pour block per grid) d’où une taille de matrice \(\mathtt{n\times n}\) où \(\mathtt{n=32\times 316=10112}\). Ce qui accélère le calcul est que des blocs des matrices A et B sont placés en mémoire partagée et qu’ensuite, les produits ligne par colonnes sont effectués en utilisant la mémoire partagée. Plus précisément, chaque kernel crée deux tableaux sA et sB dans la mémoire partagée (lignes 11-12) chacun de taille BLOCK \times BLOCK. Le thread en cours d’exécution calcule le coefficient de C en position (ty, tx) de son bloc de thread (lignes 20-21). Pour cela, il place dans la mémoire partagée :
- la valeur du coefficient de
Asitué dans le bloc en colonneiet en position \(\mathtt{(ty, tx)}\) dans le tableausA(ligne 26) - la valeur du coefficient de
Bsitué dans le bloc en ligneiet en position \(\mathtt{(ty, tx)}\) dans le tableausB(ligne 27)
Tous les threads du même bloc de la grille s’éxécutent simultanément donc
- le bloc situé à la même ligne de bloc que le bloc que le kernel exécute et à la colonne de bloc
ide la matriceAest exactement contenu dans le tableausA - le bloc situé à la même colonne de bloc que le bloc que le kernel exécute et à la ligne de bloc
ide la matriceBest exactement contenu dans le tableau sB.
Avant que la suite ne s’exécute (les produits ligne par colonne), il faut être certain que tous les threads aient recopié les valeurs. C’est pour cela qu’est écrite ligne 29 une instruction de synchronisation de ces threads. Cela correspond à ce qu’on appelle une barrière en programmation multithread.
Ensuite, est effectué le calcul ligne par colonne (ligne 32) qui lui se fait en mémoire partagée. Mathématiquement, le produit matriciel est en fait réalisé comme un produit par blocs.
Noter que le produit ligne par colonne ne fait pas intervenir que les coefficients des tableaux en mémoire partagé définis dans le kernel lui mais aussi dans les autres kernels du même bloc. C’est pour ça qu’il y a une instruction de synchronisation ligne 34
Noter également, biene que ce soit un problème d’une autre nature, qu’il n’est pas possible de définir dynamiquement les dimensions d’un tableau en mémoire partagée (lignes 11-12), elles doivent être connues à la compilation. Ainsi un code tel que
@cuda.jit('(int64[:,:], int64[:,:], int64[:,:])')
def cuda_square_mat_mult(A, B, C):
block = 32
sA = cuda.shared.array(shape=(block, block), dtype=int64)
engendrera une erreur à la compilation.
Selon mes propres essais, il ne semble pas nécessaire de faire une étape de précompilation (warmup) comme on fait avec Numba en mode jit.
Avec quelques précautions, le code ci-dessus pourrait être modifié pour s’appliquer à des matrices de taille qui ne soit pas un multiple de 32, par exemple 10000.
Un autre algorithme ?¶
Pour information, le produit de deux matrices de taille 10000 calculé en un seul processus par un algorithme de Strassen optimisé met plus de 3 min 30 s. Voici le code sous SageMath :
# SageMath et lib flint2
n=10000
p=10000
q=10000
start=time()
A=random_matrix(ZZ,n,p, x=-10, y=10)
B=random_matrix(ZZ,p,q, x=-10, y=10)
delta = time() - start
print(f"Durée : {delta:.2f}s")
start=time()
A*B
delta = time() - start
print(f"Durée : {delta:.2f}s")
Durée : 18.86s
Durée : 219.95s
Installer Cupy et comparer¶
Cupy est un module Python qui met à disposition des bibliothèque Cuda en Python. On peut facilement installer Cupy sur Google Colab. On commence par chercher la version de Cuda disponible :
!nvcc -V
qui affiche
nvcc: NVIDIA (R) Cuda compiler driver
Copyright (c) 2005-2019 NVIDIA Corporation
Built on Sun_Jul_28_19:07:16_PDT_2019
Cuda compilation tools, release 10.1, V10.1.243
en sorte qu’on peut essayer d’installer la version de Cupy adaptée à Cuda 10.1 :
!pip install cupy-cuda101
qui produit l’affichage (légèrement remanié) suivant
Collecting cupy-cuda101
Downloading https://files.pythonhosted.org/packages/\
d6/0d/37b5e06d198778b3c8163a4ee01a64bf0832300c5a738f85c7ae5ada4fb7/\
cupy_cuda101-7.7.0-cp36-cp36m-manylinux1_x86_64.whl (366.5MB)
|█████████████████████████|
366.5MB 42kB/s
Requirement already satisfied: numpy>=1.9.0 in
/usr/local/lib/python3.6/dist-packages (from cupy-cuda101) (1.18.5)
Requirement already satisfied: fastrlock>=0.3 in
/usr/local/lib/python3.6/dist-packages (from cupy-cuda101) (0.5)
Requirement already satisfied: six>=1.9.0 in
/usr/local/lib/python3.6/dist-packages (from cupy-cuda101) (1.15.0)
Installing collected packages: cupy-cuda101
Successfully installed cupy-cuda101-7.7.0
Le GPU disponible est :
from numba import cuda
print(cuda.detect())
Found 1 CUDA devices
id 0 b'Tesla P100-PCIE-16GB' [SUPPORTED]
compute capability: 6.0
pci device id: 4
pci bus id: 0
Summary:
1/1 devices are supported
True
Il ne reste plus qu’à tester le temps d’exécution du produit de deux matrices :
from time import time
import numpy as np
from numba import cuda, int64
import cupy as cp
BLOCK = 32
BOUND = 10
@cuda.jit('(int64[:,:], int64[:,:], int64[:,:])')
def cuda_square_mat_mult(A, B, C):
sA = cuda.shared.array(shape=(BLOCK, BLOCK), dtype=int64)
sB = cuda.shared.array(shape=(BLOCK, BLOCK), dtype=int64)
n, _ = A.shape
bpg = n // BLOCK
x, y = cuda.grid(2)
tx = cuda.threadIdx.x
ty = cuda.threadIdx.y
acc = 0
for i in range(bpg):
if x < n and y < n:
sA[ty, tx] = A[y, tx + i * BLOCK]
sB[ty, tx] = B[ty + i * BLOCK, x]
cuda.syncthreads()
for j in range(BLOCK):
acc += sA[ty, j] * sB[j, tx]
cuda.syncthreads()
if x < n and y < n:
C[y, x] = acc
def make_data(bpg):
n = BLOCK * bpg
A = np.random.randint(low=-BOUND, high=BOUND + 1,
size=(n, n), dtype=np.int64)
B = np.random.randint(low=-BOUND, high=BOUND + 1,
size=(n, n), dtype=np.int64)
C = np.zeros(shape=(n, n), dtype=np.int64)
return A, B, C
def square_mat_mult(A, B, C, bpg):
dA = cuda.to_device(A)
dB = cuda.to_device(B)
dC = cuda.to_device(C)
start = time()
cuda_square_mat_mult[(bpg, bpg), (BLOCK, BLOCK)](dA, dB, dC)
cuda.synchronize()
end = time()
# print("Inside Device : %.2fs" % (end - start))
dC.to_host()
return C
def cp_matmul(A, B):
A=cp.asarray(A)
B=cp.asarray(B)
C = A @ B
cp.cuda.Device().synchronize()
return cp.asnumpy(C)
def test(bpg):
n = BLOCK * bpg
A, B, C=make_data(bpg)
start = time()
C=square_mat_mult(A, B, C, bpg)
end = time()
print("Numba : %.2fs" % (end - start))
start = time()
D=cp_matmul(A, B)
end = time()
print("Cupy : %.2fs" % (end - start))
return C, D
bpg = 316
n = BLOCK * bpg
print("n =", n)
for _ in range(3):
C, D=test(bpg)
print(np.array_equal(C, D))
print("----------------")
qui affiche
n = 10112
Numba : 5.67s
Cupy : 1.07s
True
----------------
Numba : 5.67s
Cupy : 1.07s
True
----------------
Numba : 5.64s
Cupy : 1.07s
True
----------------
On est dans un rapport de 1 à 6, c’est plutôt correct si on compare d’une part le code relativement naïf et peu optimisé écrit directement en Python et d’autre part un code de bibliothèque professionnelle optimisé et écrit en C++.
Aparté mathématique¶
Ci-dessous, je tente d’expliquer d’où vient le petit calcul que l’on rencontre dans les programmes ou la littérature, sorte d’idiome standard Cuda, pour calculer le nombre de blocs pour recouvrir une matrice.
Soient \(\mathtt{n>0}\) et \(\mathtt{d>0}\) des entiers. On cherche le plus petit entier \(\mathtt{N\geq 0}\) tel que \(\mathtt{Nd\geq n}\) :
Par exemple, supposons \(\mathtt{d=10}\). Alors si \(\mathtt{n=42}\) on a \(\mathtt{N=5}\) et si \(\mathtt{n=40}\) alors \(\mathtt{N=4}\)
Autrement dit, on cherche à mettre bout à bout le moins de segments de longueur \(\mathtt{d}\) possibles en partant de 0 pour que le dernier segment recouvre \(\mathtt{n}\). Définissons le quotient et le reste : \(\mathtt{q=n//d}\) et \(\mathtt{r=n \% d}\). Il est immédiat que :
- si \(\mathtt{r=0}\) alors \(\mathtt{N=q}\)
- si \(\mathtt{r\neq 0}\) alors \(\mathtt{N=q+1}\)
En Python ou en C++, on pourrait se contenter de la formule \(\mathtt{N=q+(r!=0)}\).
Donnons cependant une formule plus mathématique, celle qui est donnée dans les documents Cuda. Vérifions que la formule \(\mathtt{N=(n+d-1)//d}\) marche dans les deux cas :
- si \(\mathtt{n=dq}\) alors \(\mathtt{n+d-1=dq+(d-1)}\) et comme \(\mathtt{0\leq d-1<d}\) on a bien \(\mathtt{(n+d-1)//d=q}\)
- si \(\mathtt{n=dq+r}\) alors \(\mathtt{n+d-1=d(q+1)+(r-1)}\) et comme \(\mathtt{0\leq r-1<r<d}\) on a bien \(\mathtt{(n+d-1)//d=q+1}\).
On peut aussi exprimer \(\mathtt{N}\) en fonction de la partie entière supérieure : \(\mathtt{N=\left \lceil{\frac nd}\right \rceil}\). En effet, d’une manière générale, \(\mathtt{\left \lceil{x}\right \rceil}\) est le plus petit entier supérieur ou égal à \(\mathtt{x}\) .
Alternative de démonstration¶
Ce qui suit n’a d’intérêt que du point de vue mathématique et peut-être ignoré. Il s’agit juste de montrer comment on pouvait trouver la formule directement.
Si \(\mathtt{n\leq d}\) alors \(\mathtt{N=1}\) . On suppose désormais que \(\mathtt{n>d}\) ce qui entraîne que \(\mathtt{N\geq 1}\). Alors comme \(\mathtt{N}\) est le plus petit entier vérifiant la propriété, \(\mathtt{N-1}\) ne la vérifie pas et comme \(\mathtt{N-1\geq 0}\), c’est que \(\mathtt{(N-1)d<n}\)
Montrons que \(\mathtt{N}\) est forcément le plus grand entier qui vérifie \(\mathtt{(N-1)d<n}\). En effet, puisque pour tout entier \(\mathtt{M>N-1}\) et donc, puisque \(\mathtt{M}\) et \(\mathtt{N}\) sont des entiers, forcément tels que \(\mathtt{M\geq N}\), on a \(\mathtt{Md\geq Nd\geq n}\).
Réciproquement, si \(\mathtt{N}\) est le plus grand entier qui vérifie \(\mathtt{(N-1)d<n}\) alors forcément, comme \(\mathtt{N+1}\) ne vérifie pas la condition, on a \(\mathtt{Nd\geq n}\) et \(\mathtt{N}\) est forcément le plus petit entier qui vérifie cette propriété puisque si \(\mathtt{M<N}\) alors (inégalité entre entiers) \(\mathtt{M\leq N-1}\) donc \(\mathtt{Md\leq (N-1)d<n}\).
Donc, finalement, on cherche le plus grand entier \(\mathtt{N}\) tel que \(\mathtt{(N-1)d<n}\) ou encore, puisque c’est une inégalité entre entiers, tel que \(\mathtt{(N-1)d\leq n-1}\) donc \(\mathtt{Nd\leq n+d-1}\) et on sait que le plus grand entier \(\mathtt{N}\) qui vérifie cela est le quotient de la division entière \(\mathtt{(n+d-1)//d}\) ce qui redonne le résultat vu plus haut.
Introspection Cuda¶
Les bibliothèques Cuda fournissent de nombreux outils d’introspection statique et dynamique (profilage) et de débogage. Ci-dessous, le programme fournit quelques données :
from numba.cuda.cudadrv import enums
from numba import cuda
from numba.cuda.cudadrv import enums
from numba import cuda
device = cuda.get_current_device()
print(device.name)
attribs= [name.replace("CU_DEVICE_ATTRIBUTE_", "") for name in
dir(enums) if name.startswith("CU_DEVICE_ATTRIBUTE_")]
for attr in attribs:
print(attr, '=', getattr(device, attr))4
dont voici seulement un extrait :
b'GeForce GTX 970'
...
MAX_BLOCK_DIM_X = 1024
MAX_BLOCK_DIM_Y = 1024
MAX_BLOCK_DIM_Z = 64
MAX_GRID_DIM_X = 2147483647
MAX_GRID_DIM_Y = 65535
MAX_GRID_DIM_Z = 65535
MAX_THREADS_PER_BLOCK = 1024
Par exemple, comme signalé plus haut, le nombre maximal de threads par blocs (1024). Ou encore les trois dimensions maximales de la grille, le nombre maximal de threads suivant l’axe des x, etc.
Je n’ai pas réussi à déterminer par ce moyen la mémoire disponible sur le GPU.